鸢(yuān)尾花(Iris)数据集介绍
鸢【音:yuān】尾花(Iris)是单子叶百合目花卉,是一种比较常见的花,而且鸢尾花的品种较多,在某个公园里你可能不经意间就能碰见它。
鸢尾花数据集最初由Edgar Anderson 测量得到,而后在著名的统计学家和生物学家R.A Fisher于1936年发表的文章「The use of multiple measurements in taxonomic problems」中被使用,用它作为线性判别分析(Linear Discriminant Analysis)的一个例子,证明分类的统计方法。该数据集是在机器学习领域一个常用的数据集。
数据中的两类鸢尾花记录结果是在加拿大加斯帕半岛上,在同一天的同一个时间段,使用相同的测量仪器,在相同的牧场上由同一个人测量出来的。这是一份有着70年历史的数据,虽然老,但是却很经典,详细数据集可以在UCI 数据库(http://archive.ics.uci.edu/ml/datasets/Iris) 中找到。

http://archive.ics.uci.edu/static/public/53/iris.zip
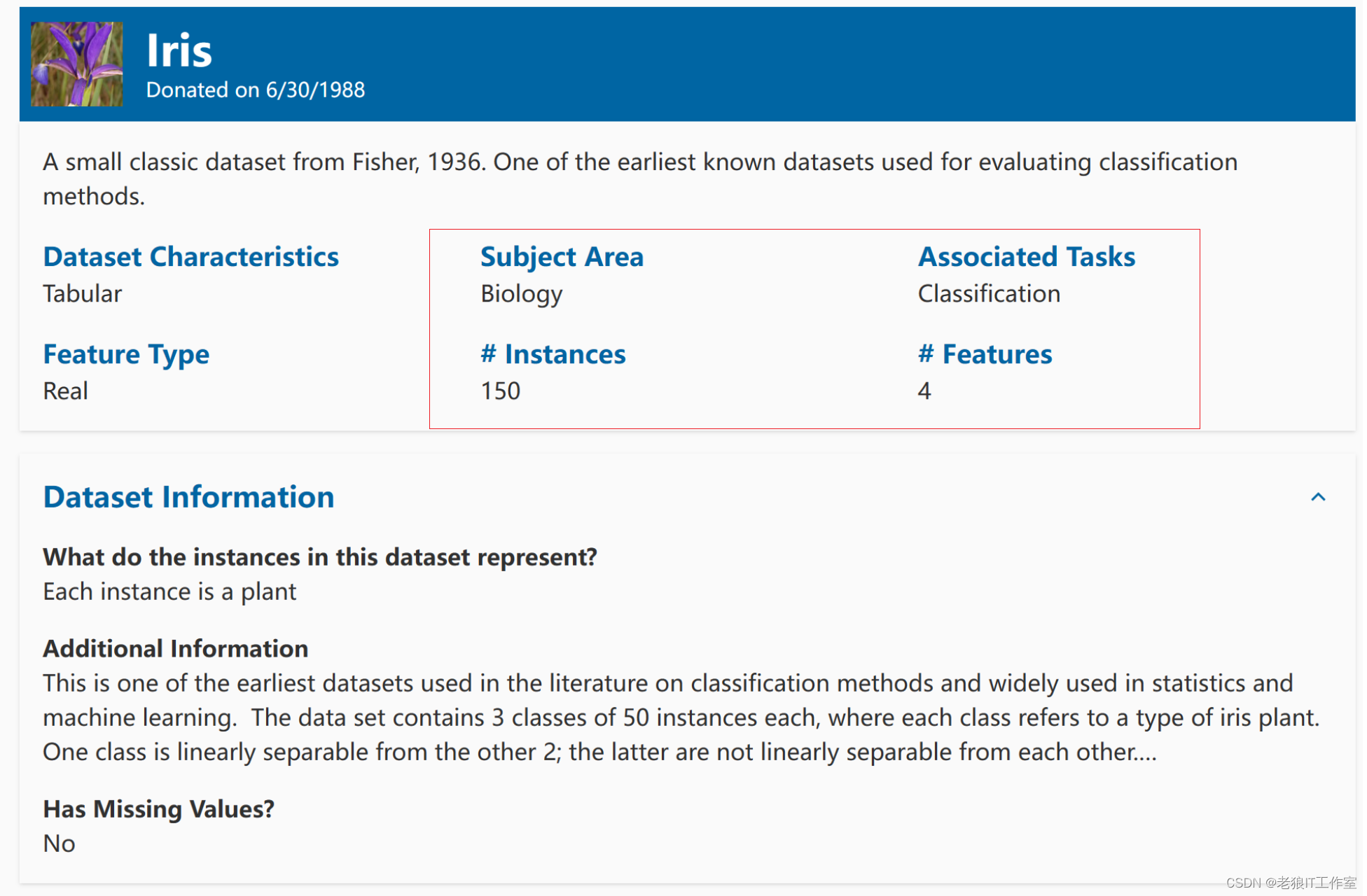
Iris也称鸢尾花卉数据集,是一类多重变量分析的数据集。通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa(山鸢尾),Versicolour(杂色鸢尾),Virginica(维吉尼亚鸢尾))三个种类中的哪一类。
鸢尾花(iris)数据集,它共有4个属性列和一个品种类别列:sepal length(萼片长度)、sepal width(萼片宽度)、petal length(花瓣长度)、petal width (花瓣宽度),单位都是厘米。3个品种类别是Setosa、Versicolour、Virginica,样本数量150个,每类50个。
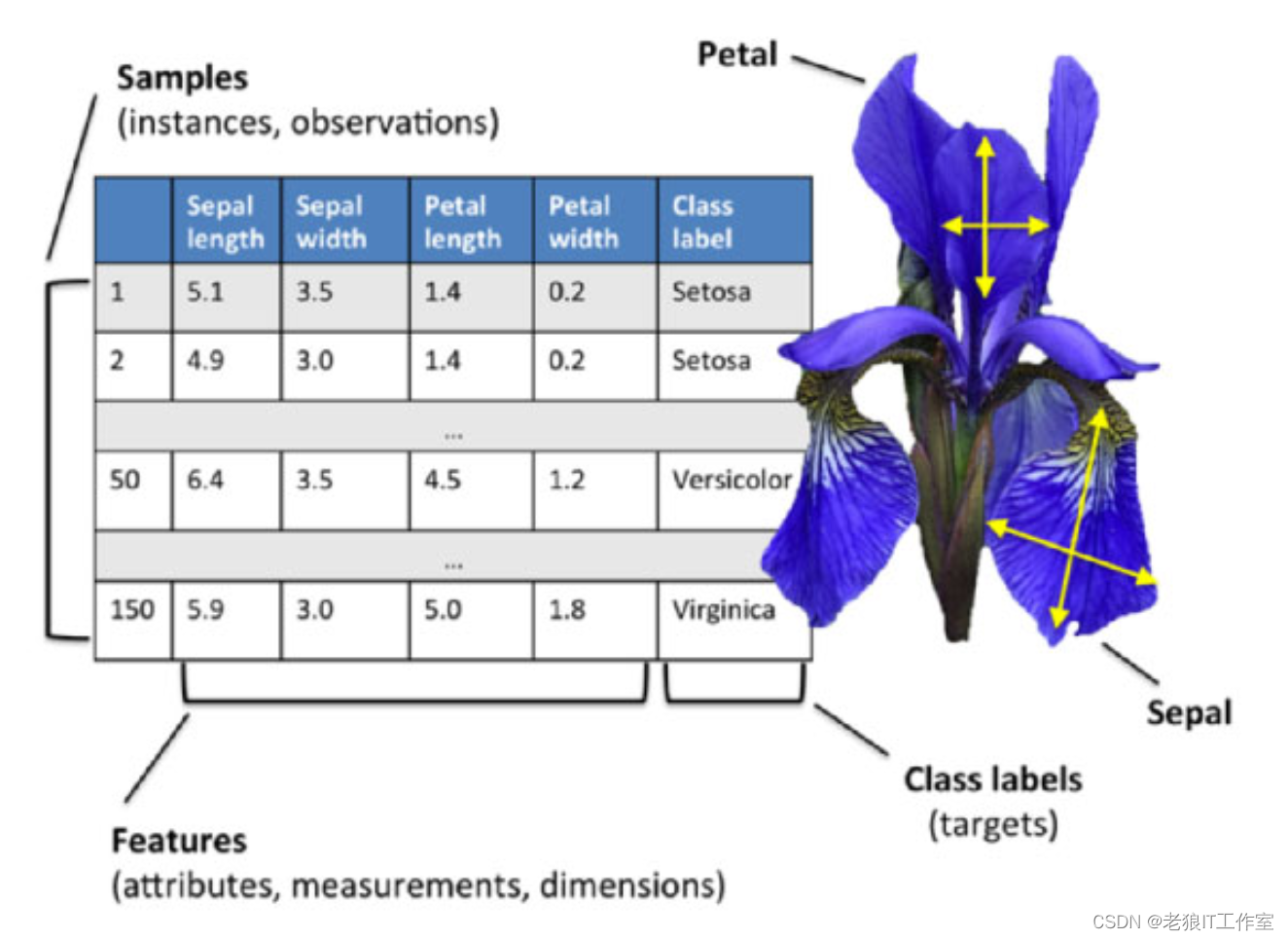
本文主要通过Jupyter Notebook对鸢尾花数据集(Iris)进行读取,显示数据,并对数据可视化,最后使用该数据集来应用于K近邻算法线性回归分析。
1)读取数据包括scikit-learn库引入和读取.csv文件保存的数据集。
2)显示数据包括显示具体数据、查看整体数据信息、描述性统计。
3)数据可视化包括散点图、直方图、KDE图、箱线图等。
4)应用该数据集于scikit-learn的K近邻算法进行线性回归分析。
读取数据
from sklearn import datasets
import pandas as pdiris_datas = datasets.load_iris()iris_df = pd.DataFrame(iris_datas.data, columns=['Sepal Length', 'Sepal Width', 'Petal Length', 'Petal Width'])# 它是一个很小的数据集,仅有150行,5列。该数据集的四个特征(1~4)列属性的取值都是数值型的,
# 他们具有相同的量纲,不需要你做任何标准化的处理,
# 第五列为通过前面四列所确定的鸢尾花所属的类别名称。
iris_csv_url = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"
names = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'class']
iris_csv_df = pd.read_csv(iris_csv_url, names=names)显示数据
基本数据信息
# 四列数据分别为
# 列1 - Sepal Length Cm: 花萼长度, 单位cm;
# 列2 - Sepal Width Cm: 花萼宽度, 单位cm;
# 列3 - Petal Length Cm: 花瓣长度, 单位cm
# 列4 - Petal Width Cm; 花瓣宽度, 单位cm
iris_datas.data[0:10]
iris_df.head()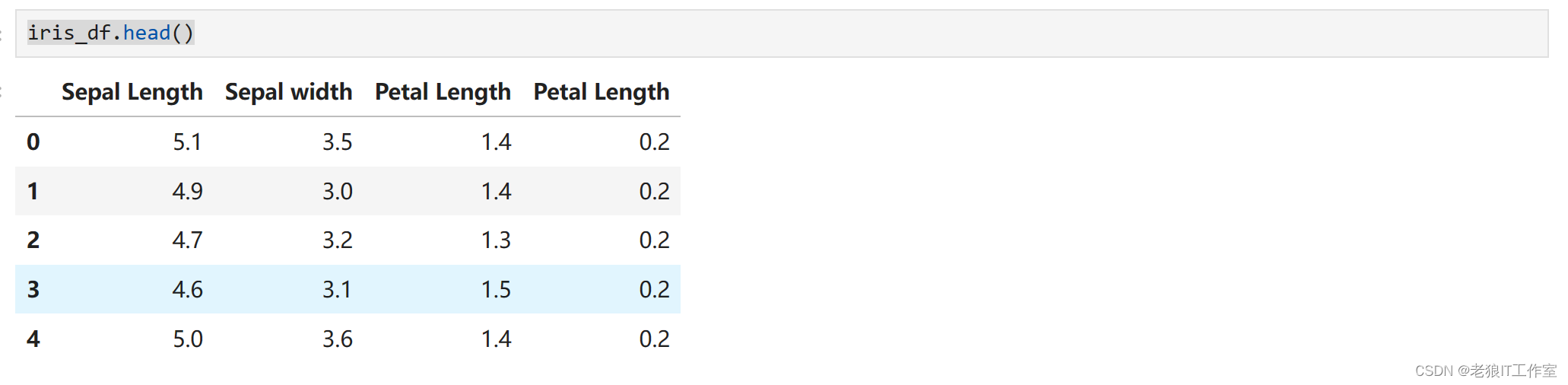
iris_datas.data.shapeiris_df.shape
# Sepa Length Cm: 花萼长度, 单位cm;
# Sepal Width Cm: 花萼宽度, 单位cm;
# Petal Length Cm: 花瓣长度, 单位cm
# Petal Width Cm; 花瓣宽度, 单位cm
iris_datas.feature_namesiris_datas.target[0:5]iris_datas.target.shapeiris_datas.target_names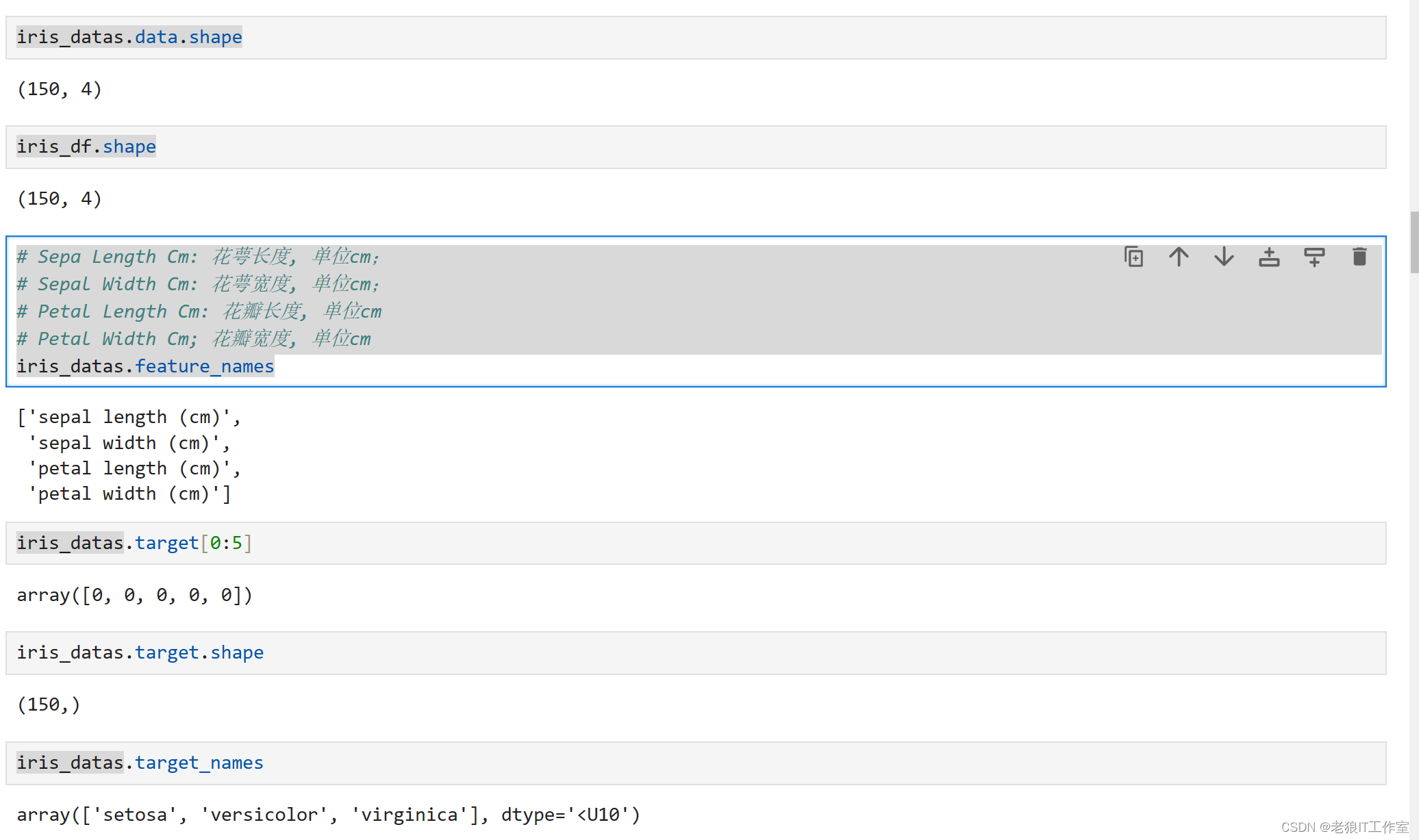
print(iris_datas.DESCR)
iris_csv_df.head()
查看数据整体信息
iris_df.info()
查看描述性统计
iris_df.describe()iris_df.describe().T 数据可视化
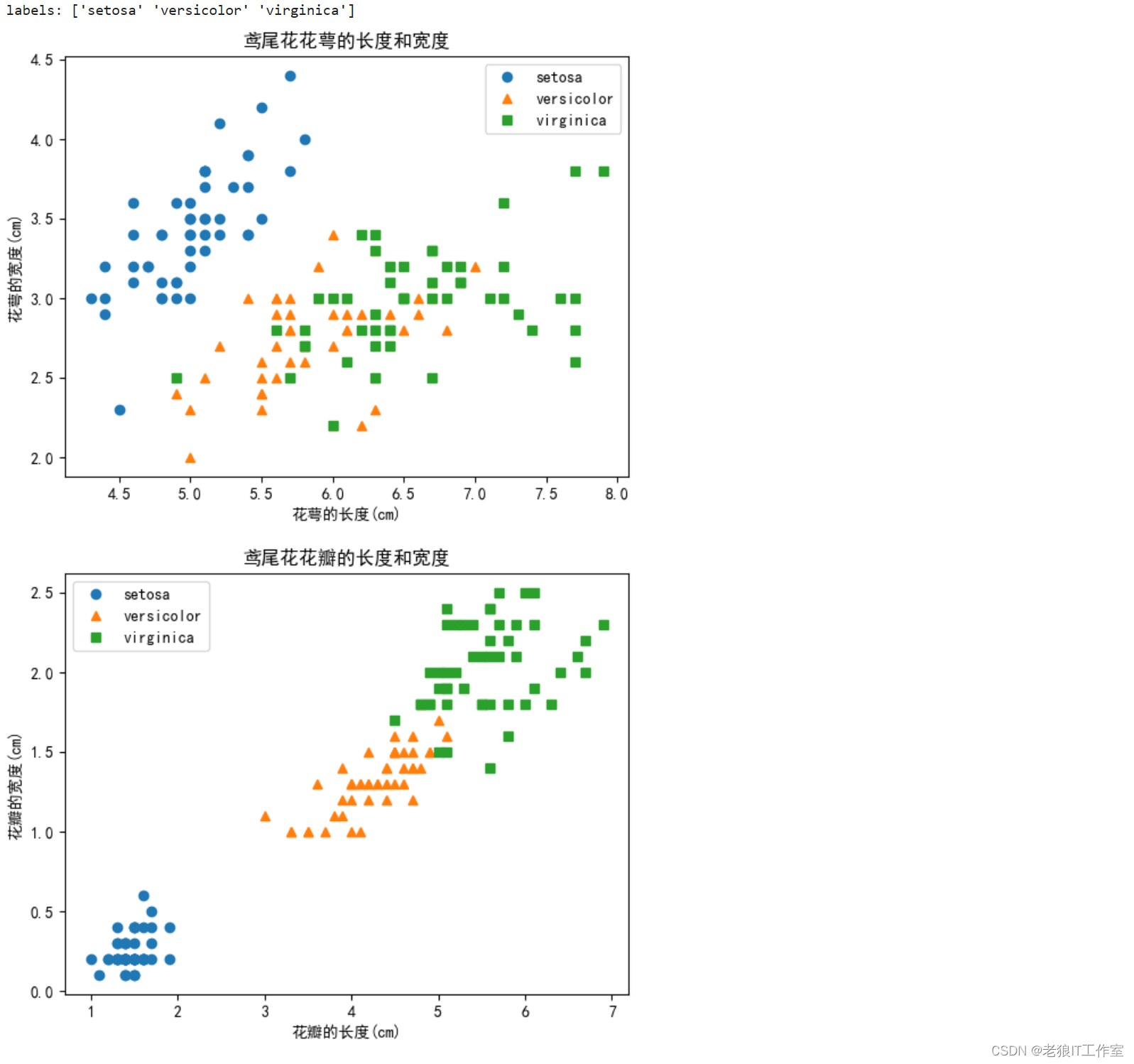
花萼长度与宽度分布 / 花瓣长度与宽度分布(用颜色和形状区分类型)
from collections import Counter, defaultdict
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei'] # 支持中文字体style_lst = ['o', '^', 's'] # 三个分类设置点的不同形状,不同形状默认颜色不同
data = iris_datas.data
labels = iris_datas.target_names
print('labels:', labels)
cls_dict = defaultdict(list) # 使用默认字典来进行分类,每个分类的数据放到一个单独的列表中
for i, d in enumerate(data):cls_dict[labels[int(i/50)]].append(d) # 一共3个种类,每一种类有50个样本集# print('col_dict:\n', col_dict)
for col in [0, 2]: # 一共4列; 1,2列为一组(花萼的长与宽);3,4列为一组(花瓣的长和宽)cls_list = []for i, (cls, cls_ds) in enumerate(cls_dict.items()):# 共3个分类draw_data = np.array(cls_ds)plot = plt.plot(draw_data[:, col], draw_data[:, col+1], style_lst[i])cls_list.append(cls)plt.legend(cls_list)plt.title('鸢尾花花瓣的长度和宽度') if col==2 else plt.title('鸢尾花花萼的长度和宽度')plt.xlabel('花瓣的长度(cm)') if col==2 else plt.xlabel('花萼的长度(cm)')plt.ylabel('花瓣的宽度(cm)') if col==2 else plt.ylabel('花萼的宽度(cm)')plt.show()[Python] 内置类defaultdict(默认字典)介绍和使用场景(案例)-CSDN博客
数据直方图
iris_csv_df.hist() #数据直方图histograms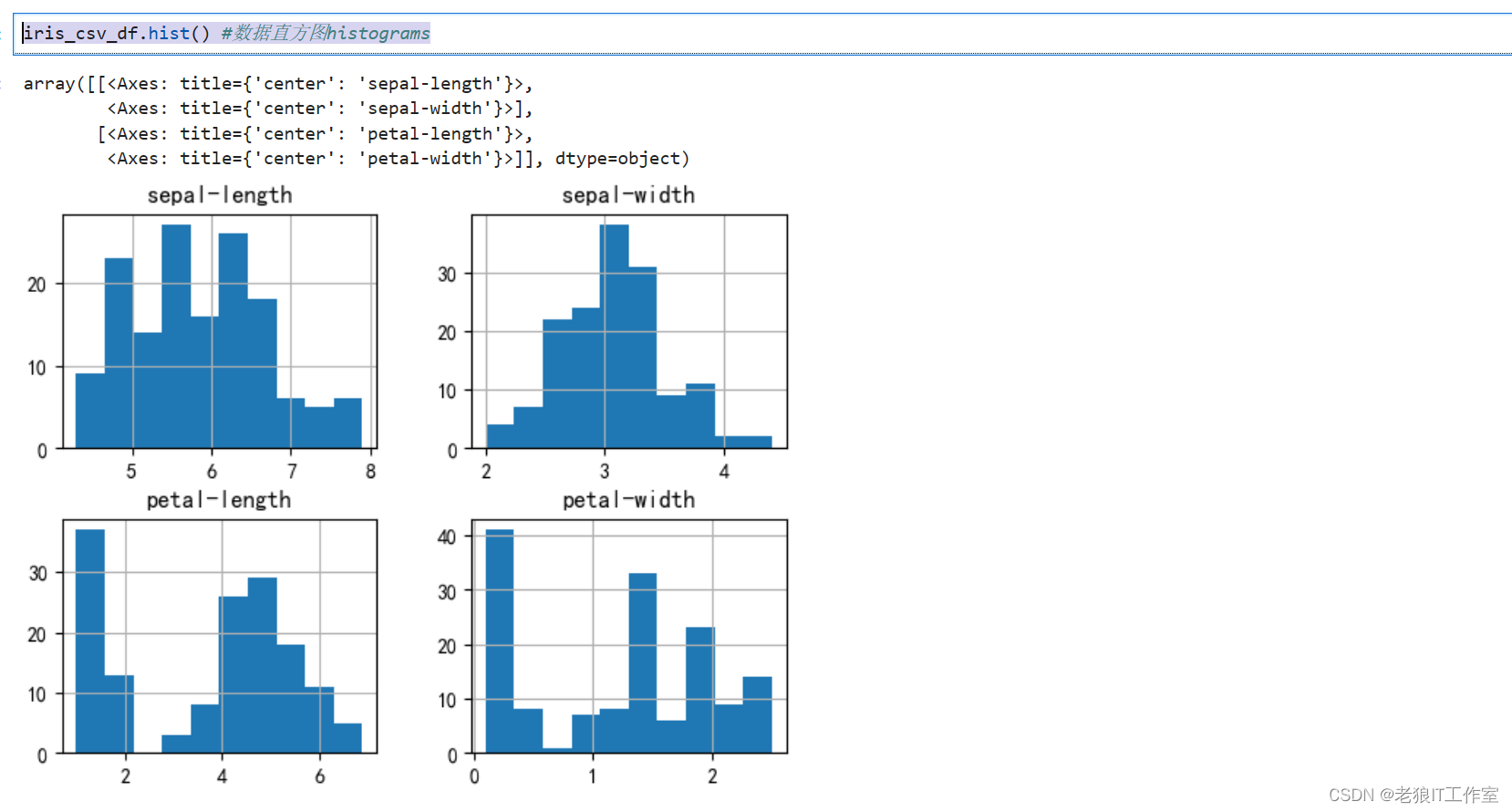
散点图(这里不区分是哪个类型)
x轴表示sepal-length花萼长度,y轴表示sepal-width花萼宽度
iris_csv_df.plot(x='sepal-length', y='sepal-width', kind='scatter')
x轴表示patal-length花瓣长度,y轴表示patal-width花瓣宽度
iris_csv_df.plot(x='petal-length', y='petal-width', kind='scatter')
KDE图
KDE图也被称作密度图(Kernel Density Estimate,核密度估计)。
KDE可以理解为是对直方图的加窗平滑。通过KDE分布图,可以查看并对训练数据集和测试数据集中特征变量的分布情况。[Python] KDE图[作密度图(Kernel Density Estimate,核密度估计)]介绍和使用场景(案例)-CSDN博客
plt.rcParams['axes.unicode_minus'] = False # 避免 UserWarning: Glyph 8722 (\N{MINUS SIGN}) missing from current font.
iris_csv_df.plot(kind='kde') 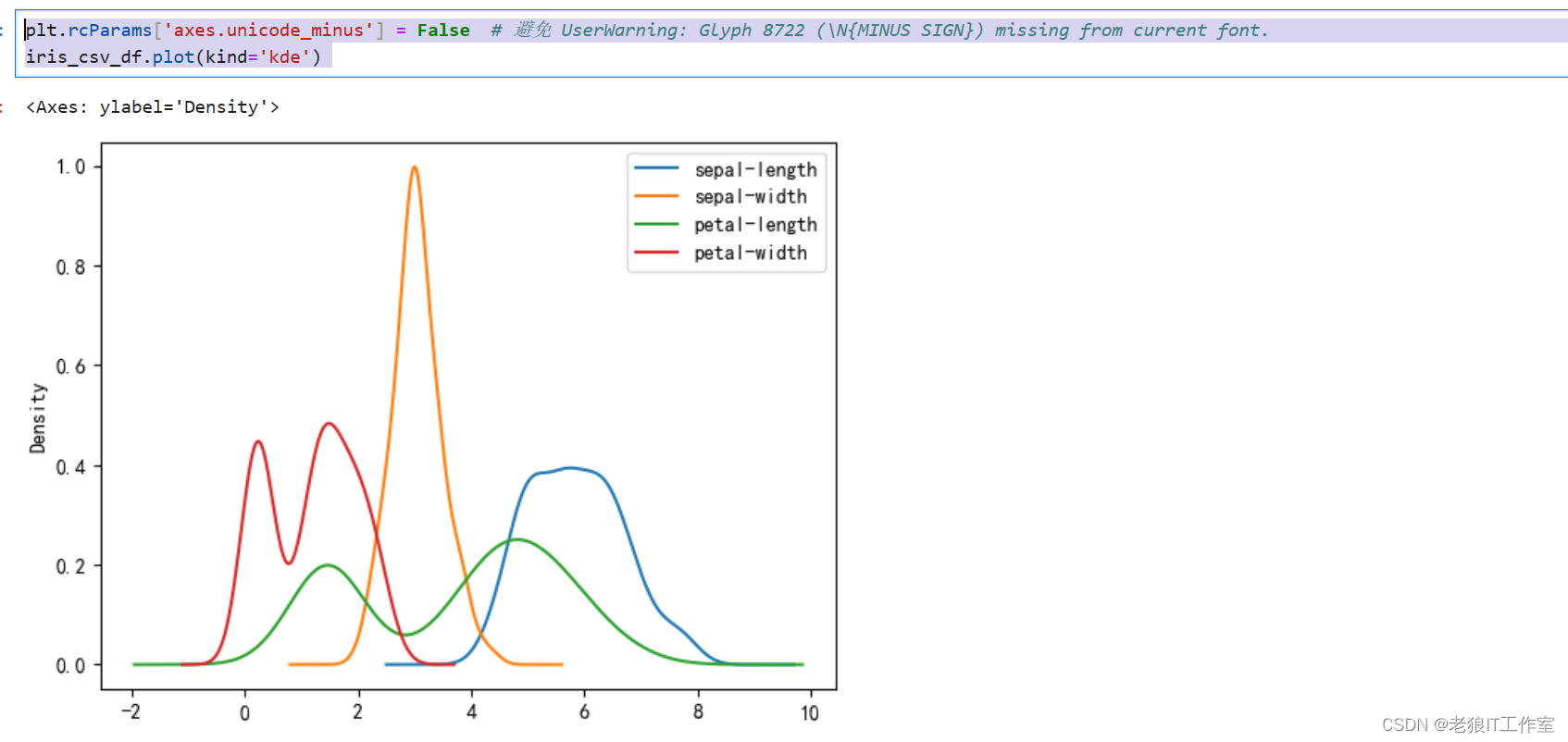
与对应的直方图进行对比一下:
iris_csv_df.plot(kind='hist') 
箱线图
kind='box’绘制箱图,包含子图且子图的行列布局layout为2*2,子图共用x轴、y轴刻度标签为False。
iris_csv_df.plot(kind='box', subplots=True, layout=(2,2), sharex=False, sharey=False)
根据iris数据集使用K近邻算法进行线性回归
[Python] scikit-learn - K近邻算法介绍和使用案例-CSDN博客








)



)





)

