树

前面文章讲的线性表，不论数组还是链，都是“一对一”的关系，本文章节让我们来认识一下“一对多”关系的数据结构——树（Tree）。
树结构分为二叉树和三叉树等，如下图所示。常用的就是二叉树，因此本节以二叉树为主要介绍对象，二叉树之外的树结构暂且统称为非二叉树。

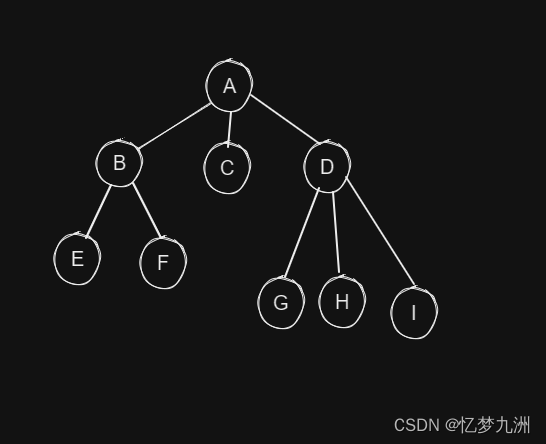
树在数据结构中占据重要的地位。对于树结构的学习其实不难，先了解它的概念和性质，然后结合图示去理解，最后亲自动手实现其功能，按照这样的思路去学习，一定可以轻松掌握。

• 节点：用树存储的每一个数据元素都称为节点；
• 父节点：也叫双亲节点，某一节点的上一个节点即为其父节点，如在上图中，A是B、C、D的父节点，B是E、F的父节点；
• 子节点：与父节点相反，在上图中，B、C、D是A的子节点，E、F是B的子节点；
• 兄弟节点：拥有同一个父节点的若干节点互为兄弟节点，如在上图中，B、C和D 互为兄弟节点；
• 根节点：每棵非空树有且只有一个根节点，如上图中的A节点；
• 叶子节点：也叫叶节点，指没有子节点的节点，如图3.18中的C、E、F、G、H和I节点；
• 空树：没有节点的树就是空树；
• 子树：只包含该节点某一 子节点下所有节点的树称为该节点的子树，其有左子树（leftsubtree）和右子树（rightsubtree）之分；
• 森林：拥有若干棵互不相交的树的集合；
• 度：一个节点拥有的子节点数（子树数）；
• 层次：根节点为第一层，根节点的子节点为第二层，以此类推；
• 深度：也叫高度，即树中节点层次的最大值；
• 有序树：有顺序的树，即对哪个节点在左边及哪个节点在右边有明确规定的树；
• 无序树：没有限制节点顺序的树。

注意：一棵树的度，是树内各节点的度的最大值。

二叉树

下面让我们来了解一下二叉树的相关知识吧。
二叉树的定义很简单：其一，它是有序树；其二，各节点的度（子节点数）均不超2。但是二叉树的功能却不简单。
二叉树又分为普通二叉树、对称二叉树、满二叉树和完全二叉树，如下图所示。由于各种树之间可相互转化，所以按道理它们均可使用顺序存储和链式存储，但鉴于空间使用率，普通二又树和对称二叉树一般使用链式存储。

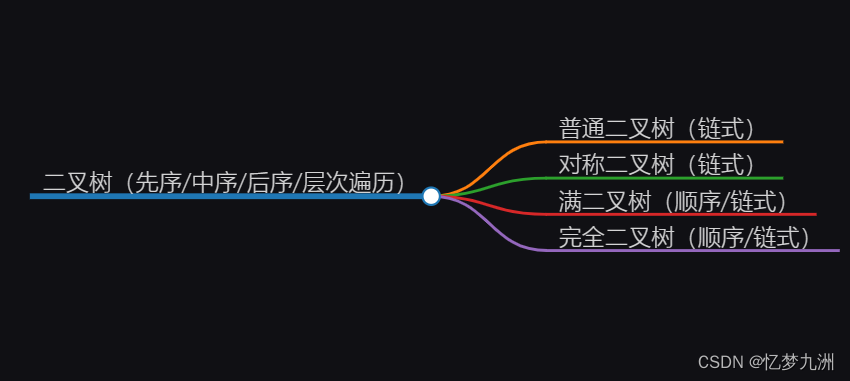
1. 普通二叉树

普通二叉树其实就是二叉树，只是为了将二叉树更好地分类，才在这里为其加上“普通”二字，以下简称为二叉树，如下图所示。

二叉树的性质如下：

• 二又树的第i层最多有$2i-1$ 个节点;
• 二又树最多有$2k-1$个节点，k为该树的深度；
• 二双树的叶子节点数$n_0$比度为2的节点数$n_2$多1，即$n_0$=$n_2$+1。

对于第3个性质，很多人肯定有疑问：看似毫无关联的 $n_0$和$n_2$，不可能只相差1吧?其实很好证明。我们知道，树的每个节点头上都有一条分路（根节点除外），于是可以得到等式：
$$总节点数=总路数+1$$
$$总节点数即n_0+n_1+n_2，总路数即n_1+2n_2，于是可得：$$
$$n_0+n_1+n_2=n_2+2n_2+1$$
化简可得：
$$n_0=n_2+1$$

2. 对称二叉树

如果某二叉树根节点的左右子树互为镜像，则称其对称二叉树。或者换个说法，某二又树与其镜像是完全一致的，则称其对称二叉树，如下图所示。

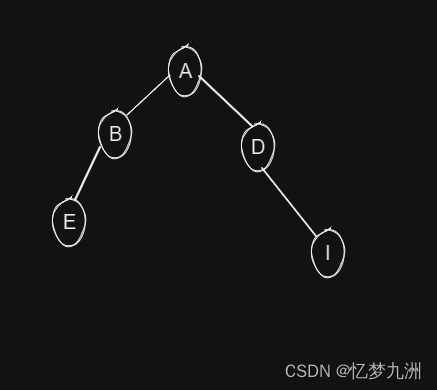
3. 满二叉树

满二叉树有两种定义；一种是指所有节点的度为0或2的二叉树（要么“后继无人”，要么“一朝双喜”）；另一种是指深度为k，节点数为$2k-1$的二叉树（要么在最底层作叶子节点，要么就得有两个子节点，就像一个标准的三角呢）。这里以第二种定义为准进行介绍，如下图所示。

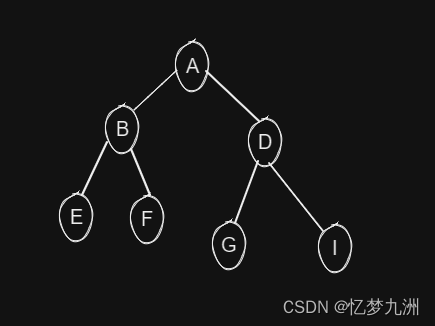
满二叉树除了具有普通二叉树的性质之外，还有以下性质：

• 第i层的节点数为 $2i-1$；
• 满二叉树的节点数必为$2k-1$，叶子数必为$2k-1$，k为该树的深度；
• 满二叉树的深度$lo{g}_2(n+1)$，n为该树的节点数；
• 所有节点的度要么为0，要么为2，并且叶子节点均在最底层。

4. 完全二叉树

完全二叉树由满二叉树演变而来。如果二叉树从根节点到倒数第二层为满二叉树，并且最底层的节点均靠左对齐，则这个二又树为完全二叉树。显而易见，满二叉树一定是完全二叉树，如下图所示。
完全二叉树同样具有二叉树的所有性质，并且其深度为$\lfloor lo{g}_{2}k\rfloor +1$，k为该树的节点数。

注意：$\lfloor \rfloor$表示向下取整，如$\lfloor lo{g}_{2}4\rfloor$和$\lfloor lo{g}_{2}5\rfloor$均等于2。

如果将完全二又树的节点按照先从上到下再从左到右的顺序进行标号，那就更有意思了：
（1）若i＞1，节点i的父节点为节点$\lfloor i/2\rfloor$；
（2） 若2i＞n，则节点i为叶子节点，n为该树的节点数；
（3）若2i+1＞n，则节点；无右子节点，n为该树的节点数；
（4）若节点i有子节点，则其左孩子为$2i$，右孩子为$2i+1$。
如果用数组来实现已标号的完全二又树，则变成了“推”（Heap）。