💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述
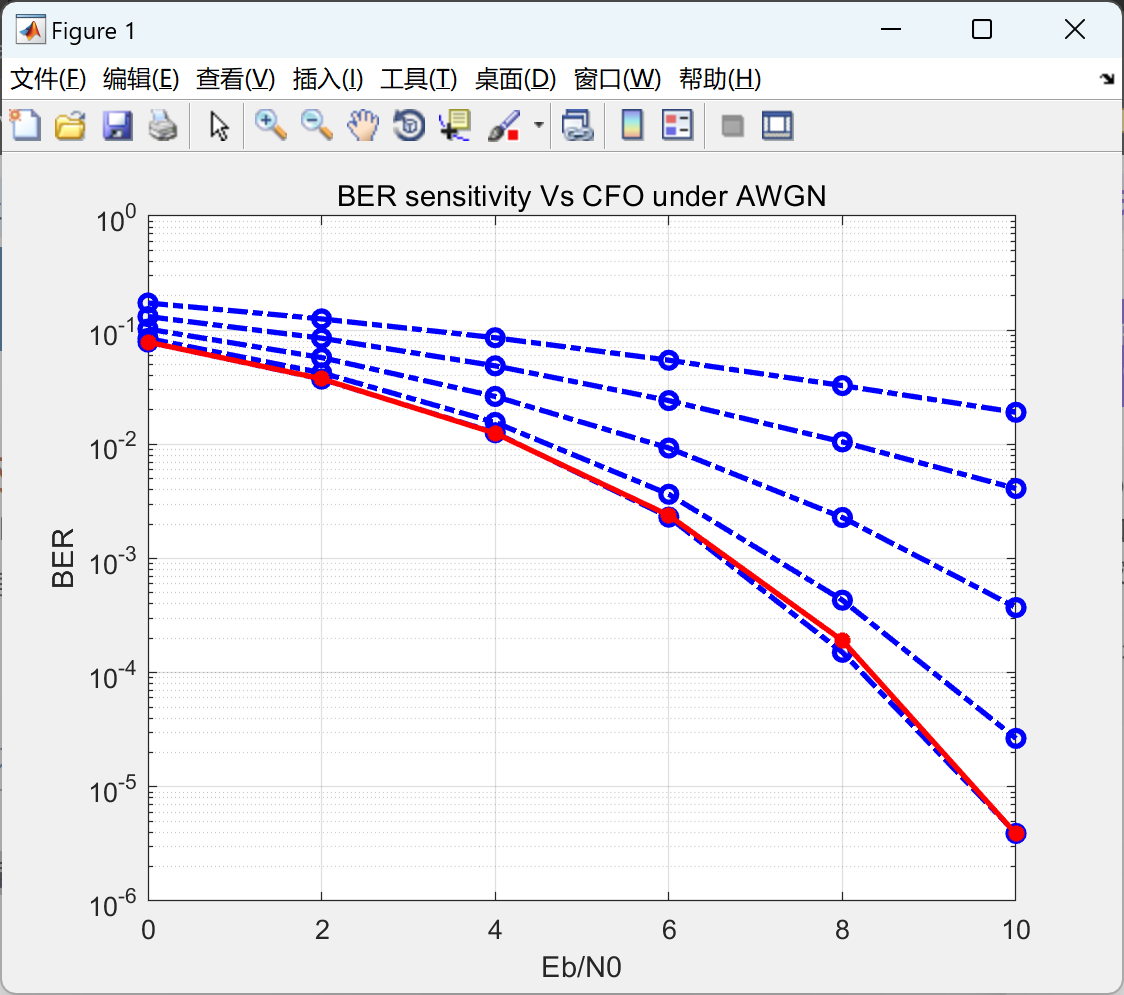
OFDM系统是一种常用的调制技术,可以有效地抵抗多径衰落和频率选择性衰落等信道影响。然而,当OFDM系统遇到载波频率偏移(CFO)时,其性能可能会受到影响。
CFO是指接收端的载波频率与发送端的载波频率之间存在的偏移。这种偏移可能是由于时钟不同步、多普勒效应或其他因素引起的。CFO会导致接收端无法正确地对接收到的信号进行解调,从而影响系统的性能。
在AWGN信道下,OFDM系统对CFO的BER灵敏度可以通过仿真或理论分析进行研究。一种常见的方法是通过引入CFO来模拟实际情况,并测量系统在不同CFO值下的误码率(BER)。
研究表明,当CFO较小时,OFDM系统的性能受到的影响较小。但是随着CFO的增大,系统的性能会逐渐下降。当CFO超过一定阈值时,系统的性能可能会急剧下降,甚至无法正常工作。
为了减小CFO对OFDM系统性能的影响,可以采取一些技术手段,如引入导频信号进行载波频率估计和校正、采用自适应等化器来抵消频偏等。
总之,OFDM系统在AWGN信道下对不同载波频率偏移(CFO)的BER灵敏度研究可以帮助我们了解系统的性能限制,并为系统设计和性能优化提供指导。
📚2 运行结果
部分代码:
xt = 2*x -1;
xt = (nFFT/sqrt(nDSC))*ifft(fftshift(xt),nFFT); % else use 'measured' awgn
xtt = [xt(end-nCP+1:end) xt];
% Gaussian noise of unit variance, 0 mean
nt = 1/sqrt(2)*(randn(1,nTot) + 1i*randn(1,nTot));
yr = sqrt(nTot/nFFT)*xtt + 10^(-EsN0dB(n)/20)*nt;
% applying CFO
yr =(exp(1i*2*pi*CFO(ii)*(0:length(yr)-1)/nFFT)).*yr;
% Receiver processing
yr = yr(nCP+1:end);
yr = (nDSC/sqrt(nFFT))*fftshift(fft(yr,nFFT));
yr = yr > 0; % demodulating
berrors = berrors + length(find((yr-x)~=0));
end
toc;
BER(ii,n) = berrors/(nFFT*MC);
end
end
semilogy(EbN0dB,BER,'-.ob','LineWidth',2); hold on; grid on;
title('BER sensitivity Vs CFO under AWGN');
% theoratical calculations
dataenc = 'nondiff';
EbNo = EbN0dB;
M = 2;
ThBer = berawgn(EbNo,'psk',M,dataenc);
semilogy(EbNo, ThBer,'-*r','LineWidth',2); xlabel('Eb/N0');ylabel('BER');
🎉3 参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。
[1]周鹏,赵春明,史志华,等.AWGN信道中载波频偏影响下的PCC-OFDM系统性能分析[J].中国科学(E辑:信息科学), 2007, 37(10):1339.DOI:10.1360/zf2007-37-10-1339.
[2]隋天宇,李宇,袁兆凯,等.OFDM系统中一种载波频率偏移估计与补偿方法研究[C]//中国声学学会青年学术会议.2009.DOI:ConferenceArticle/5aa0093cc095d72220634e05.

)

)

)

)



)







)
