遍历二叉树

封面：遍历二叉树.png

王有志，一个分享硬核Java技术的互金摸鱼侠
加入Java人的提桶跑路群：共同富裕的Java人

今天我们继续学习数据结构与算法的内容，主要是如何遍历一棵二叉树，那么我们直接开始吧。

创建二叉树

在数据结构：认识一棵树的最后我们声明了链式存储结构的树，现在为其添加上构造方法：

public class TreeNode<E> {private E element;private TreeNode<E> leftChild;private TreeNode<E> rightChild;public TreeNode(E element, TreeNode<E> leftChild, TreeNode<E> rightChild) {  this.element = element;  this.leftChild = leftChild;  this.rightChild = rightChild;  }
}

这样，就可以创建一棵如下的树了：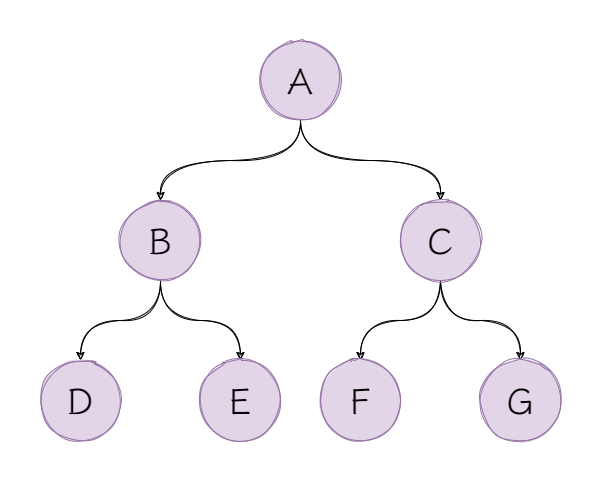
图1：一棵二叉树.png
代码如下：

TreeNode<String> tree = new TreeNode<>("A", new TreeNode<>("B", new TreeNode<>("D", null, null), new TreeNode<>("E", null, null)), new TreeNode<>("C", new TreeNode<>("F", null, null), new TreeNode<>("G", null, null)));

虽然代码看着很闹心，不过还是先忍一忍，下一篇我们就开始构建可以“真正”使用的树。
如果你动手实现过链表你就会知道，链表的所有操作基本上都是围绕着遍历进行的，对于使用链式存储结构的树来说，操作也是基于遍历来实现的。
那么我们该如何遍历一棵树呢？毕竟它不像链表那样是线性结构，树是有分叉的，搞不好就跑偏了。

遍历二叉树

既然容易跑偏，那么我们就规定一下遍历的路径，防止大家跑偏。可以将二叉树的遍历分为两大类：

深度优先遍历
- 前序遍历
- 中序遍历
- 后序遍历
广度优先遍历
- 层序遍历

深度优先遍历中深度指的是树的深度，从根节点出发，优先按照指定的顺序访问左子树的，然后再访问右子树。
广度优先遍历中广度指的是树每层的度，同样从根节点出发，按照每层从左至右的方式访问，结束后进入下一层。

前序遍历

前序遍历的顺序是：

访问根节点；
访问左子树；
访问右子树；
访问子树时，按照同样的顺序执行。

我们来看看前序遍历的顺序是怎样的：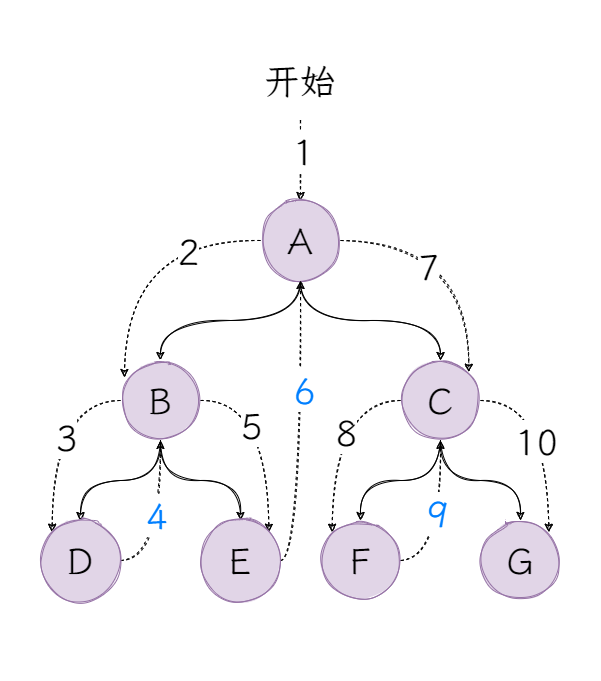
图2：前序遍历.png
特别说明：蓝色编号的路径，代表经过但不访问。
首先是访问根节点A，接着访问左子树BDE的根节点B，再访问子树BDE的左子树D，子树D没有子节点，开始访问子树BDE的右子树E，之后重复以上步骤，直至访问到G。
流程我们已经了解了，那么具体实现肯定是不在话下了。
首先从根节点A进入，按照根-左-右的顺序，如果指针移动到了子树BDE的根节点B，那么会丢失子树CFG，所以我们可以创建一个容器存储子树CFG。那么该使用哪种容器呢？别着急，我们接着往下看。
假设我们此时已经选好了容器，并且放入了子树CFG，此时开始遍历子树BDE，同样的需要将子树BDE的右子树E放入到容器中，此时容器中有子树CFG和子树E。当访问子树D之后，开始访问栈中的子树，按照前序遍历的顺序，需要访问子树E，到这里相信你已经知道要使用哪种结构了吧？
通过迭代实现的二叉树前序遍历代码如下：

public void preorderTraversal(TreeNode<E> root) {Stack<TreeNode<E>> treeNodeStack = new LinkedStack<>();while (root != null || treeNodeStack.size() != 0) {while (root != null) {System.out.print(root.element + " ");treeNodeStack.push(root.rightChild);root = root.leftChild;}root = treeNodeStack.pop();}
}

中序遍历

中序遍历的顺序是：

访问左子树；
访问根节点；
访问右子树；
访问子树时，按照同样的顺序执行。

再来看看中序遍历的顺序是怎样的：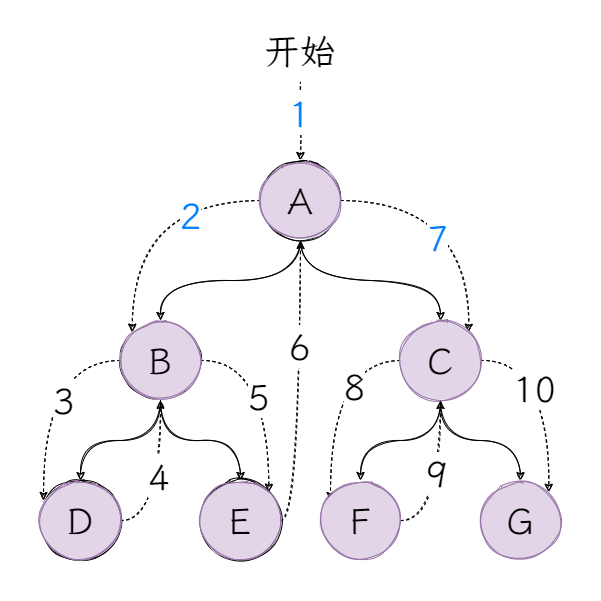
图3：中序遍历.png
首先经过根节点A，按照中序遍历的顺序，并不访问根节点A，访问左子树BDE，套用中序遍历的顺序，经过左子树BDE的根节点B，开始访问左子树D，子树D没有左子节点，访问节点D，子树D没有右子节点，访问左子树BDE的根节点B，接着访问左子树BDE的右子树E，之后重复以上步骤，直至访问到G。
中序遍历和前序遍历不一样的是，前序遍历是将未访问的右子树放入到栈中，而中序遍历是将树的整棵左斜树放入到栈中，然后依次取出按照左-根-右的顺序进行访问。

public void inorderTraversal(TreeNode<E> root) {Stack<TreeNode<E>> treeNodeStack = new LinkedStack<>();while (root != null || treeNodeStack.size() != 0) {while (root != null) {treeNodeStack.push(root);root = root.leftChild;}root = treeNodeStack.pop();System.out.print(root.element + " ");root = root.rightChild;}
}

提示：在第一次内循环入栈时，从栈底到栈顶的元素依次是ABD，此时节点D不再看做是子树D的根节点，而是看做子树BDE的左子节点。

后序遍历

了解了前序遍历，中序遍历后你有没有猜到后序遍历是怎样一种顺序？
是的，在深度优先遍历中，前中后序指的是访问根节点的顺序，先访问就是前序遍历，在访问左右子树之间访问就是中序遍历，最后访问就是后序遍历。
那么，后序遍历的顺序是：

访问左子树；
访问右子树；
访问根节点；
访问子树时，按照同样的顺序执行。

同样还是一张图展示后序遍历的顺序：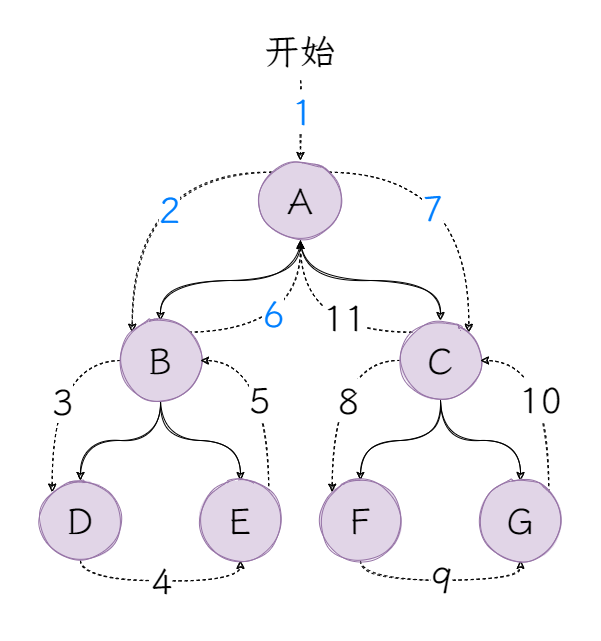
图4：后序遍历.png
首先经过根节点A，按照后序遍历的顺序，不访问根节点A，访问左子树BDE的左子节点D，访问左子树BDE的右子节点E，访问左子树BDE的根节点B，接着访问右子树CFG，之后重复以上步骤，直至访问到根节点A。
后序遍历和中序遍历一样，第一次内循环仍旧是将整棵左斜树放入栈中，不过后序遍历的顺序是左-右-根，此时需要先访问右子节点。
在这里我们逐步拆解代码，大部分代码都和中序遍历一样：

public void postorderTraversal(TreeNode<E> root) {Stack<TreeNode<E>> treeNodeStack = new LinkedStack<>();while (root != null || treeNodeStack.size() != 0) {while (root != null) {treeNodeStack.push(root);root = root.leftChild;}// 处理访问逻辑}
}

后序遍历的关键点在于处理访问逻辑的部分。
在第一次内循环后，栈中是ABD，此时节点D出栈，假设按照处理中序遍历的逻辑，直接访问后修改root指向：

root = treeNodeStack.pop();
System.out.print(root.element + " ");
root = root.rightChild;

那么接下来出栈的是节点B，但是直接访问B的话顺序就错了。我们站在子树BDE的视角来看，此时节点D已经被访问，按照顺序来说，是要访问节点E，但此时root == node_B，刚开始我想到直接访问root.rightChild后将B再放回去不就好了吗？

root = treeNodeStack.pop();
if(root.rightChild != null) {root = root.rightChild;treeNodeStack.push(root);
} else {System.out.print(root.element + " ");
}

如果这么做了，即便节点B出栈了，栈中依旧是AB，下次再进入不就死循环了吗？
我们需要标记B的是否二次入栈，如果是二次入栈，就直接访问。那么为TreeNode添加status字段可以吗？
图5：可以，但没必要.png
因为除了拥有左右子节点的节点外，还有一部分节点是可以直接访问的，比如说：DEFG。
除了标记状态外，我们还有什么办法可以得知二次入栈的节点是否直接访问？很简单，我们只需要知道上一次访问的是不是其右子节点即可。
我们可以在外循环外声明一个节点，记录访问过的节点：

TreeNode<E> prev = null;

那么访问逻辑该怎么写呢？现在我们先再捋一捋，什么情况下直接访问root：

root.rightChild == null
root.rightChild == prev

好了，所有的逻辑都跃然纸上了，后序遍历的整体代码如下：

public void postorderTraversal(TreeNode<E> root) {Stack<TreeNode<E>> treeNodeStack = new LinkedStack<>();TreeNode<E> prev = null;while (root != null || treeNodeStack.size() != 0) {while (root != null) {treeNodeStack.push(root);root = root.leftChild;}root = treeNodeStack.pop();if (root.rightChild == null || root.rightChild == prev) {System.out.print(root.element + " ");prev = root;root = null;} else {treeNodeStack.push(root);root = root.rightChild;}}
}

终极优雅

到目前为止，我们已经通过迭代实现了二叉树的深度优先遍历。但是你看看，又是while又是if的，还有嵌套循环，一点都不优雅。
那么有没有更优雅的方式呢？
记得数据结构：优雅的删除链表元素吗？在文章的最后，我们通过递归实现了“终极优雅”，那么二叉树的遍历是不是也可以通过递归呢？
答案是肯定的。不知道通过上面的内容，你有没有感受到二叉树是一种天然的递归结构。从根节点开始，可以划分多个子树，甚至叶子节点也可以认为是没有子节点的树的根节点。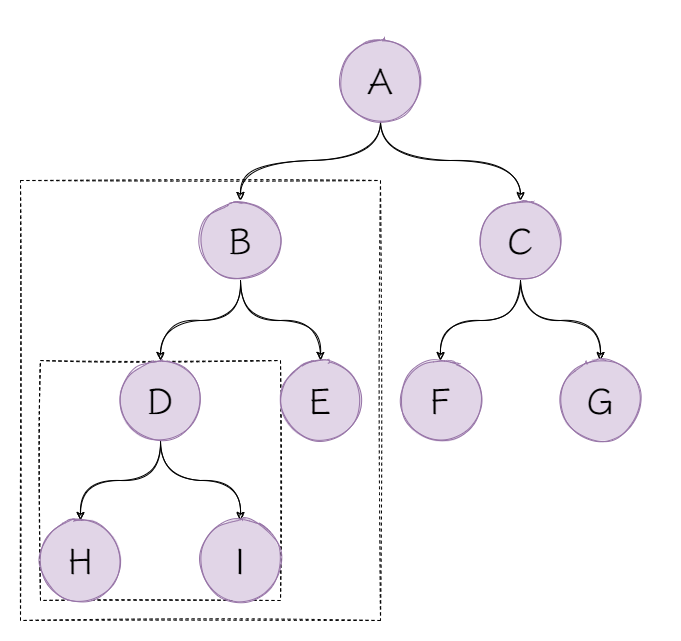
图6：二叉树的子树.png
我们再来提示下递归的特点，递归是将复杂的问题拆分成简单的问题后求解合并的过程。这应该是第三次提到递归的特点了。
图7：重要的事情说三遍.png
那么这就好办了，我们不断地拆分这棵二叉树，直到最左叶子节点，然后逐步解决问题不就可以了吗？
先来改写一下前序遍历，首先是处理边界情况root == null，然后根据前序遍历的特点，直接访问根节点即可：

public void preorderTraversal(TreeNode<E> root) {if(root == null) {return null;}System.out.print(root.element + " ");
}

这样，我们完成了第一个根节点的访问，接着的顺序是什么？访问左子树，然后是右子树，那么全部的代码已经跃然纸上了：

public void preorderTraversal(TreeNode<E> root) {if(root == null) {return null;}System.out.print(root.element + " ");preorderTraversal(root.leftChild);// 1preorderTraversal(root.rightChild);// 2
}

是不是看着有点懵？我们逐步拆解来看一下，假设我们要处理的树如下：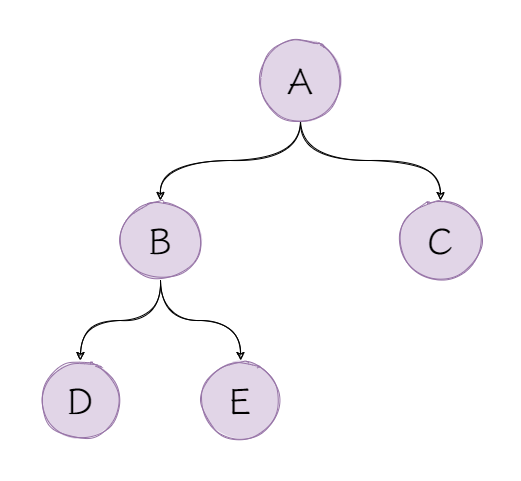
图8：简单的二叉树.png

第1次调用，入参A：
- 访问A
- 调用编号1代码，此时编号2代码挂起；
第2次调用，入参B（A.leftChild）：
- 访问B
- 调用编号1代码，此时编号2代码挂起；
第3次调用，入参D（B.leftChild）：
- 访问D
- 调用编号1代码，此时编号2代码挂起；
第4次调用，入参null（D.leftChild）：
- 返回null
- 返回第3次调用，调用编号2代码；
第5次调用，入参E（B.leftChild）：
- 访问E
- 调用编号1代码，此时编号2代码挂起；
- ……

经过多次递归后，二叉树的前序遍历结束。到目前，我们也通过递归实现了二叉树的前序遍历，如果还是懵懵的状态，可以动手在纸上写出来每次调用的过程，方便理解。至于中序遍历和后序遍历，相信你一定可以想到。

层序遍历

层序遍历是将二叉树分层后，按照从左至右的顺序访问每层的元素。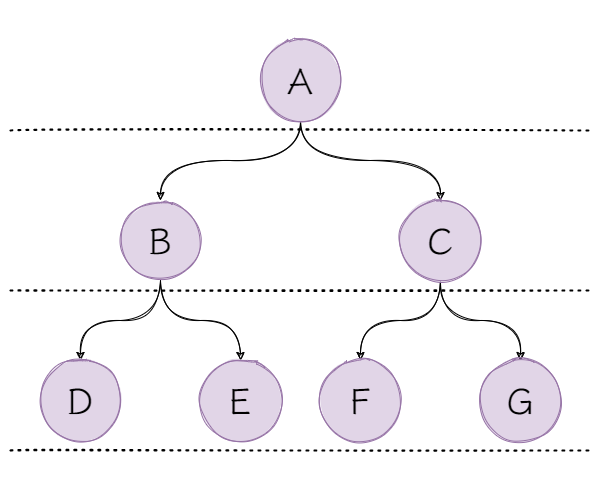
图9：层序遍历.png
层序遍历就没办法使用二叉树的递归性了，我们需要从每层开始，逐步的从左向右开始遍历。
例如，访问节点A，之后访问节点B（A.leftChild），再然后是节点C（A.rightChild），以此类推，直到访问到节点G。
可以创建一个容器，存储即将访问的节点，比如，在访问节点A时，将节点B，C放入容器，此时容器存储B，C，访问节点B时，将节点D，节点E放入容器，此时容器内存储C，D，E，先放入的先访问，显然最合适的容器是队列。
代码也是非常容易的：

public void levelOrder(TreeNode<E> root) {if(root == null) {return;}Queue<TreeNode<E>> nodes = new SinglyLinkedQueue<>();nodes.add(root);while (!nodes.isEmpty()) {TreeNode<E> currentNode = nodes.poll();System.out.print(currentNode.element + " ");if(currentNode.leftChild != null) {nodes.add(currentNode.leftChild);}if(currentNode.rightChild != null) {nodes.add(currentNode.rightChild);}}
}

这里就不过多解释了，相信你一看就能明白，更多相关内容，会放到图的广度优先搜索中说明。

结语

今天我们一起学习了二叉树的遍历，分别通过迭代和递归实现了二叉树的深度优先遍历，迭代的方式是比较符合人的思维，所以我们开始就会铆足劲从迭代入手，但是容易忽略借助其他数据结构，而递归更符合计算机的思维，初次接触并不容易想到，还需要多加练习来熟悉递归。
最后借助队列实现了二叉树的层序遍历，过程还是比较简单的，不过多赘述了，比较有难度的一点是如何将层序遍历的结果输出为二维结构，大家可以试一下力扣上面的题目。
特别说明：文中使用到的数据结构LinkedStack和SinglyLinkedQueue是我自己实现的，可以参考文末的代码仓库。