8.2摆动序列（LC376-M）

算法：

其实动态规划和贪心算法都能做

但是动态规划的时间复杂度是O(n^2)

贪心算法的时间复杂度是O(n)

所以学习贪心算法

到底为什么用贪心？（分析局部最优和全局最优）

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

局部最优推出全局最优，并举不出反例，那么试试贪心！

实际操作上，其实连删除的操作都不用做，因为题目要求的是最长摆动子序列的长度，所以只需要统计数组的峰值数量就可以了（相当于是删除单一坡度上的节点，然后统计长度）

遍历时，遇到摆动就++

这就是贪心所贪的地方，让峰值尽可能的保持峰值，然后删除单一坡度上的节点

对应的代码：

峰值，即前后差为一正一负，那就要计算前后差

前差： prediff = nums[i]-nums[i-1]

后差：curdiff = nums[i+1]-nums[i]

峰值：prediff<0 and curdiff > 0

实际写代码之前要考虑多种情况：

本题异常情况的本质，就是要考虑平坡，平坡分两种，一个是上下中间有平坡，一个是单调有平坡

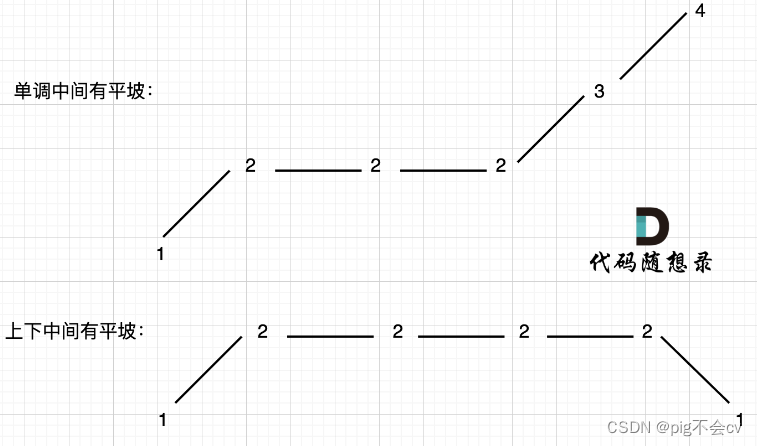
而且，求坡度至少要3个数，那还要再考虑nums只有两个数的情况。

最后一共有三种情况：

情况一：上下坡中有平坡
情况二：数组首尾两端（统计峰值的时候，数组最左面和最右面如何统计呢？题目中说了，如果只有两个不同的元素，那摆动序列也是 2。）
情况三：单调坡中有平坡

结合具体情况画坡度图分析：

1.情况一：上下坡中有平坡

例如 [1,2,2,2,1]这样的数组：

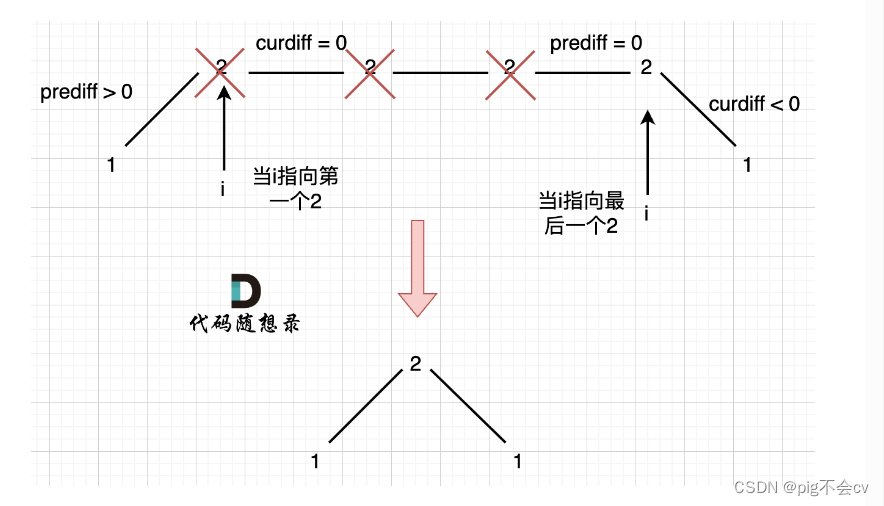
峰值：prediff==0 and curdiff<0 或者 prediff>0 and curdiff==0

情况二：数组首尾两端

判断prediff和curdiff的前提是数组至少有3个元素，那如果只有2个呢？

此时之前的规则就不好使了。

解决方法：

可以假设，数组最前面还有一个数字，那这个数字和首个数字相同，即prediff==0？（但实际代码中没有加数值这一步，只要result初始值=1就可以）

那么为了规则统一，针对序列[2,5]，可以假设为[2,2,5]，这样它就有坡度了即 preDiff = 0，如图：

result 初始为 1（默认最右面有一个峰值），此时 curDiff > 0 && preDiff <= 0，那么 result++（计算了左面的峰值），最后得到的 result 就是 2（峰值个数为 2 即摆动序列长度为 2）。

情况三：单调坡度有平坡

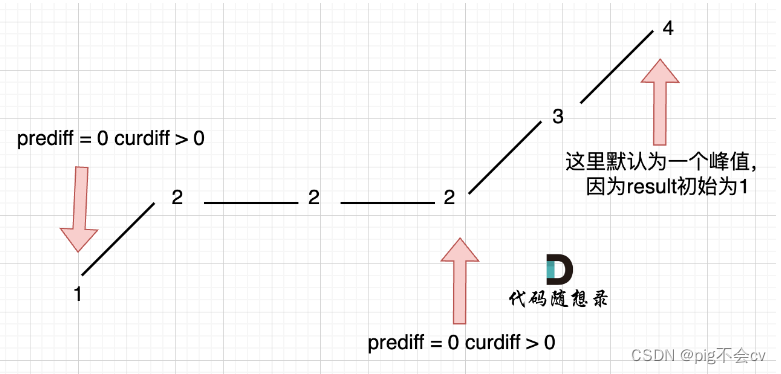
这个序列其实没有摆动，只有头尾两个值，结果应该为2。如图：prediff=0 and curdiff >0

但是在前两种情况中：prediff=0 and curdiff >0，result++，结果就会变成3，就会报错。

问题在哪？

prediff一直跟着curdiff更新：循环中，prediff = curdiff

解决方法：

不要实时更新prediff。

只需要在这个坡度摆动变化的时候，更新 prediff 就行，这样 prediff 在单调区间有平坡的时候就不会发生变化

正确代码：

class Solution {public int wiggleMaxLength(int[] nums) {//初始化int result = 1;//处理只有2个数的情况int prediff = 0;int curdiff = 0;//处理只有0\1个数的情况if (nums.length<=1) {return nums.length;}//贪心算法，局部最优-全局最优//注意：i<nums.length，不能取等！索引不到！for (int i=1;i<nums.length;i++){curdiff = nums[i]-nums[i-1];//若出现峰值,result++if (prediff >=0 && curdiff <0 || prediff <=0 && curdiff >0){result++;prediff = curdiff;}}return result;}}