在 MATLAB 中,有一个非常有用的函数
reshape,它可以将一个m x n矩阵重塑为另一个大小不同(r x c)的新矩阵,但保留其原始数据。给你一个由二维数组
mat表示的m x n矩阵,以及两个正整数r和c,分别表示想要的重构的矩阵的行数和列数。重构后的矩阵需要将原始矩阵的所有元素以相同的 行遍历顺序 填充。
如果具有给定参数的
reshape操作是可行且合理的,则输出新的重塑矩阵;否则,输出原始矩阵。示例 1:
输入:mat = [[1,2],[3,4]], r = 1, c = 4 输出:[[1,2,3,4]]示例 2:
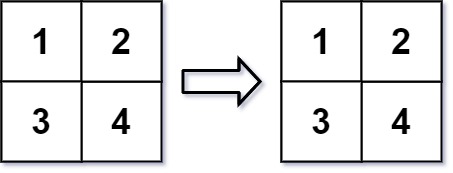
输入:mat = [[1,2],[3,4]], r = 2, c = 4 输出:[[1,2],[3,4]]提示:
m == mat.lengthn == mat[i].length1 <= m, n <= 100-1000 <= mat[i][j] <= 10001 <= r, c <= 300
试题解析
题意:给定一个二维数组a,根据给定行长列长创建新的二维数组b,将a的元素按需存入b中
解题思路:
我们要做的事情就是:
-
将二维数组 nums\textit{nums}nums 映射成一个一维数组;
-
将这个一维数组映射回 rrr 行 ccc 列的二维数组。
具体实现
- 首先将二维数组映射成[0,m*n)]的每一个整数
- 当前的映射为 (i,j)→i×n+j
- 同样的,我们可以将元素映射到矩阵中的下标
i = x / n;
j = x % n;
代码如下
class Solution {
public:vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {int m = mat.size();int n = mat[0].size();//判断两个数组空间是否相同if(m * n != r * c) return mat;vector<vector<int>> v(r,vector<int>(c));for(int i = 0;i < m * n;i ++){v[i / c][i % c] = mat[i / n][i % n];}return v;}
};

)



)








)

)
)

