1、线性回归(linear Regression)和逻辑回归(logistic Regression)的区别
线性回归主要是用来拟合数据,逻辑回归主要是用来区分数据,找到决策边界。
线性回归的代价函数常用平方误差函数,逻辑回归的代价函数常用交叉熵。
参数优化的方法都是常用梯度下降。
eg:
现有一组面积和房价的数据,现在有个朋友要卖房子,120平方米,大概能卖多少钱?
就可以通过这组数据建立一个线性模型,然后用这组数据去拟合模型,拟合完毕后,输入120,它就会告诉你朋友能卖多少钱。
补充:(这是一个监督学习,且是回归问题,回归问题指的是预测一个具体的数据输出,即房价)
补充2:(监督学习中还有一种分类问题,用来预测离散值输出,如观察肿瘤大小,来判断是良性合适恶性,输出只有两种:【0】良性,【1】恶性)
逻辑回归也被称为对数几率回归,实际上是用线性回归解决分类问题的分类模型(在线性回归的基础上,加了一层sigmoid函数,将线性函数变为非线性函数),sigmoid函数的形状呈‘S’形,它能将任意实数映射到0~1之间的某个概率值上;
线性回归一般用于数据预测,预测结果一般为实数;
逻辑回归一般用户分类预测,预测结果一般为某类可能的概率。
2、波士顿房价线性回归案例:
1)获取数据集:
在sklearn1.2版本之前,可用from sklearn.datasets import load_boston # 从读取房价数据存储在变量 boston 中。 boston = load_boston()
在sklearn1.2版本之后,因为某些原因移除了该数据集,
可用如下代码实现:
#导入波士顿房价,自版本1.2之后移除了该数据集,可以通过如下方法获取
from sklearn.datasets import fetch_openml
data_x,data_y=fetch_openml(name='boston',version=1,as_frame=True,return_X_y=True,parser='pandas')如果出现证书报错:urllib.error.URLError: <urlopen error [SSL: CERTIFICATE_VERIFY_FAILED] certi,可以加入如下代码:
#全局取消证书验证,使用fetch_opneml下载数据时候避免报错
import ssl
ssl._create_default_https_context = ssl._create_unverified_context2)划分训练集测试集:
#随机采样25%的数据构建测试样本,其余作为训练样本
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(data_x,data_y,random_state=33,test_size=0.25)
#分析回归目标值的差异:
print(np.max(data_y),np.min(data_y),np.mean(data_y))3)数据标准化:
#先导入数据标准化模块
from sklearn.preprocessing import StandardScaler
#分别初始化对特征和目标值的标准化器
ss_X=StandardScaler()
ss_Y=StandardScaler()
#分别对训练和测试数据的特征及目标值进行标准化处理
X_train=ss_X.fit_transform(X_train)
X_test=ss_X.transform(X_test)
Y_train=ss_Y.fit_transform(Y_train.values.reshape(-1,1))
Y_test=ss_Y.transform(Y_test.values.reshape(-1,1))
#reshape(-1,1)将所有行的数据化为1列
#reshape(1,-1)将所有列的数据化为1行4)用线性回归模型和随机梯度下降分别对美国波士顿房价进行预测
from sklearn.linear_model import LinearRegression
#使用默认配置初始化线性回归器LinearRegression
lr=LinearRegression()
#使用训练数据进行参数估计
lr.fit(X_train,Y_train[:,0])
print('系数:',lr.coef_)
print('偏置:',lr.intercept_)
#对测试数据进行回归预测
lr_y_predict=lr.predict(X_test)
#导入初始线性回归器
from sklearn.linear_model import SGDRegressor
sgdr=SGDRegressor()
#使用训练数据进行参数估计
sgdr.fit(X_train,Y_train[:,0])
#对测试数据集进行回归预测
sgdr_y_predict=sgdr.predict(X_test)系数&偏置:
系数: [-0.1147262 0.13081062 0.01168159 0.09047604 -0.17816355 0.3189522
-0.01783831 -0.33316307 0.26809803 -0.21757932 -0.20355027 0.05513145
-0.40687576]
偏置: 9.643684906345349e-16
5)性能评测
#使用LinearRegression模型自带的评估模块,并输出评估结果
print('The value of default measurement of LinearRegression is',lr.score(X_test,Y_test))
#从sklearn.metrics依次导入r2_score、mean_squared_error、mean_absolute_error用于回归性能评估
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
#使用r2_score模块,评估结果
print('The value of R-squared of LinearRegression is ',r2_score(Y_test,lr_y_predict))
#使用mean_squared_error模块,评估结果
print('The mean squared error of LinearRegression is ',mean_squared_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(lr_y_predict).reshape(-1,1))))
#使用mean_absolute_error模块,评估结果
print('The mean absolute error of LinearRegression is ',mean_absolute_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(lr_y_predict).reshape(-1,1))))#使用SGDRegressor模型自带的评估模块,并输出评估结果
print('The value of default measurement of SGDRegressor is',lr.score(X_test,Y_test))
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
#使用r2_score模块,评估结果
print('The value of R-squared of SGDRegressor is ',r2_score(Y_test,sgdr_y_predict))
#使用mean_squared_error模块,评估结果
print('The mean squared error of SGDRegressor is ',mean_squared_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(sgdr_y_predict).reshape(-1,1))))
#使用mean_absolute_error模块,评估结果
print('The mean absolute error of SGDRegressor is ',mean_absolute_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(sgdr_y_predict).reshape(-1,1))))
评测结果:
The value of default measurement of LinearRegression is 0.6757955014529482
The value of R-squared of LinearRegression is 0.6757955014529482
The mean squared error of LinearRegression is 25.13923652035345
The mean absolute error of LinearRegression is 3.5325325437053974
The value of default measurement of SGDRegressor is 0.6757955014529482
The value of R-squared of SGDRegressor is 0.6670953292509274
The mean squared error of SGDRegressor is 25.813859135815584
The mean absolute error of SGDRegressor is 3.5114251714191758
3、完整代码:
import pandas as pd
import numpy as np#全局取消证书验证,使用fetch_opneml下载数据时候避免报错
import ssl
ssl._create_default_https_context = ssl._create_unverified_context#导入波士顿房价,自版本1.2之后移除了该数据集,可以通过如下方法获取
from sklearn.datasets import fetch_openml
data_x,data_y=fetch_openml(name='boston',version=1,as_frame=True,return_X_y=True,parser='pandas')
#随机采样25%的数据构建测试样本,其余作为训练样本
from sklearn.model_selection import train_test_split
X_train,X_test,Y_train,Y_test=train_test_split(data_x,data_y,random_state=33,test_size=0.25)
#分析回归目标值的差异:
print(np.max(data_y),np.min(data_y),np.mean(data_y))#数据标准化
#先导入数据标准化模块
from sklearn.preprocessing import StandardScaler
#分别初始化对特征和目标值的标准化器
ss_X=StandardScaler()
ss_Y=StandardScaler()
#分别对训练和测试数据的特征及目标值进行标准化处理
X_train=ss_X.fit_transform(X_train)
X_test=ss_X.transform(X_test)
Y_train=ss_Y.fit_transform(np.array(Y_train).reshape(-1,1))
Y_test=ss_Y.transform(np.array(Y_test).reshape(-1,1))
#reshape(-1,1)将所有行的数据化为1列
#reshape(1,-1)将所有列的数据化为1行#使用线性回归模型和随机梯度下降分别对美国波士顿房价进行预测
from sklearn.linear_model import LinearRegression
#使用默认配置初始化线性回归器LinearRegression
lr=LinearRegression()
#使用训练数据进行参数估计
lr.fit(X_train,Y_train[:,0])
print('系数:',lr.coef_)
print('偏置:',lr.intercept_)
#对测试数据进行回归预测
lr_y_predict=lr.predict(X_test)
#导入初始线性回归器
from sklearn.linear_model import SGDRegressor
sgdr=SGDRegressor()
#使用训练数据进行参数估计
sgdr.fit(X_train,Y_train[:,0])
#对测试数据集进行回归预测
sgdr_y_predict=sgdr.predict(X_test)#性能评测
#使用LinearRegression模型自带的评估模块,并输出评估结果
print('The value of default measurement of LinearRegression is',lr.score(X_test,Y_test))
#从sklearn.metrics依次导入r2_score、mean_squared_error、mean_absolute_error用于回归性能评估
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
#使用r2_score模块,评估结果
print('The value of R-squared of LinearRegression is ',r2_score(Y_test,lr_y_predict))
#使用mean_squared_error模块,评估结果
print('The mean squared error of LinearRegression is ',mean_squared_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(lr_y_predict).reshape(-1,1))))
#使用mean_absolute_error模块,评估结果
print('The mean absolute error of LinearRegression is ',mean_absolute_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(lr_y_predict).reshape(-1,1))))#使用SGDRegressor模型自带的评估模块,并输出评估结果
print('The value of default measurement of SGDRegressor is',lr.score(X_test,Y_test))
from sklearn.metrics import r2_score,mean_squared_error,mean_absolute_error
#使用r2_score模块,评估结果
print('The value of R-squared of SGDRegressor is ',r2_score(Y_test,sgdr_y_predict))
#使用mean_squared_error模块,评估结果
print('The mean squared error of SGDRegressor is ',mean_squared_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(sgdr_y_predict).reshape(-1,1))))
#使用mean_absolute_error模块,评估结果
print('The mean absolute error of SGDRegressor is ',mean_absolute_error(ss_Y.inverse_transform(np.array(Y_test).reshape(-1,1)),ss_Y.inverse_transform(np.array(sgdr_y_predict).reshape(-1,1))))4、运行结果:
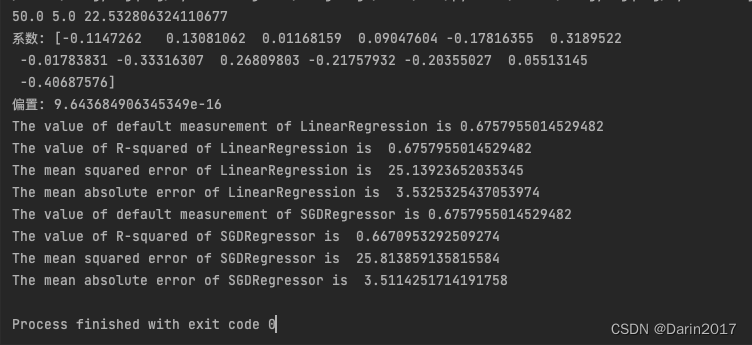
5、分析补充
从指标上,线性回归效果要略好一些,因为前者是解析法,后者是估计,如果数据规模超过10万,那么用梯度下降比较好,节省时间。



)
)

基于CNN-Bi_LSTM的多维回归预测(卷积神经网络-双向长短期记忆网络))



:模型预测)





JavaScript事件分析)


Goal-Auxiliary Actor-Critic for 6D Robotic Grasping with Point Clouds)