一、abc算法

#include "cstdio"
int main(){int a,b,c;//定义名字为a,b,c的三个整型变量for(a=0;a<=9;++a){
// a的初始值是0,当a满足a<=9的时候,可以执行循环体
//++自增的意思for(b=0;b<=9;++b){for(c=0;c<=9;++c){//abc+bcc=532//abc-->100*a+10*b+cif(100*a+10*b+c+100*b+10*c+c == 532){printf("%d %d %d\n",a,b,c);//%d是占位符 d是decimal 十进制整数}}}}
}1.1对运行遇到的问题解决
程序错误:编译错误,链接错误,运行错误
1.2 编译错误:一般程序有语法问题,如少一个“;”

1.3链接错误:一般是函数名写错了,如main写成“man”

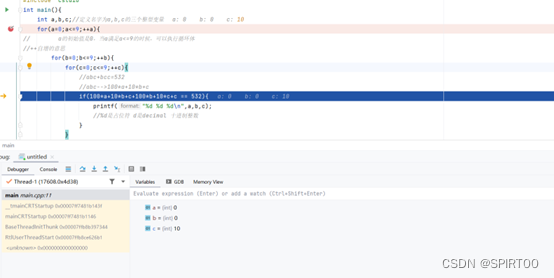
1.4当运行错误时,可进行打断点来进行调试,程序暂停观察监视窗口,点步过
二、反序数

#include "cstdio"
//int main(){
// int a,b,c;//定义名字为a,b,c的三个整型变量
// for(a=0;a<=9;++a){
a的初始值是0,当a满足a<=9的时候,可以执行循环体
++自增的意思
// for(b=0;b<=9;++b){
// for(c=0;c<=9;++c){
// //abc+bcc=532
// //abc-->100*a+10*b+c
// if(100*a+10*b+c+100*b+10*c+c == 532){
// printf("%d %d %d\n",a,b,c);
// //%d是占位符 d是decimal 十进制整数
// }
// }
//
// }
//
// }
//}
int Reverse(int n) {//名为Reverse的函数,有一个int参数,返回int类型int remain;int reverse = 0;while (true) {remain = n % 10;n = n / 10;reverse = reverse * 10 + remain;//当最后一次循环执行时,推出循环if (n == 0) {break;}}return reverse;//返回结果
}
int main(){
// int n=1234;
// int remain;
// int reverse=0;
while(n>0){
remain=n%10;//4
n=n/10;//1234->123->12
reverse=reverse*10+remain;//0->4->43
// while(true){
// remain=n%10;
// n =n/10;
// reverse =reverse*10 +remain;
// //当最后一次循环执行时,推出循环
// if(n==0){
// break;
// }int a,b,c,d;for (a = 1; a <= 9; ++a) {for (b = 0; b <= 9; ++b) {for (c = 0; c <= 9; ++c) {for (d = 0; d <= 9; ++d) {int n = 1000 * a + 100 * b + 10 * c + d;if (n*9 == Reverse(n)) {printf("%d\n",n);}}}}}
}
三、对称平方数

#include<cstdio>
int Reverse(int n){int remain;//每一次余数int reverse=0;while(true){remain=n%10;reverse=reverse*10 +remain;n=n/10;if(n==0){break;}}return reverse;
}
int main(){int i=0;for(i=0;i<=256;++i){if(i*i== Reverse(i*i)){printf("%d\n",i);}}}
四、定位死循环问题
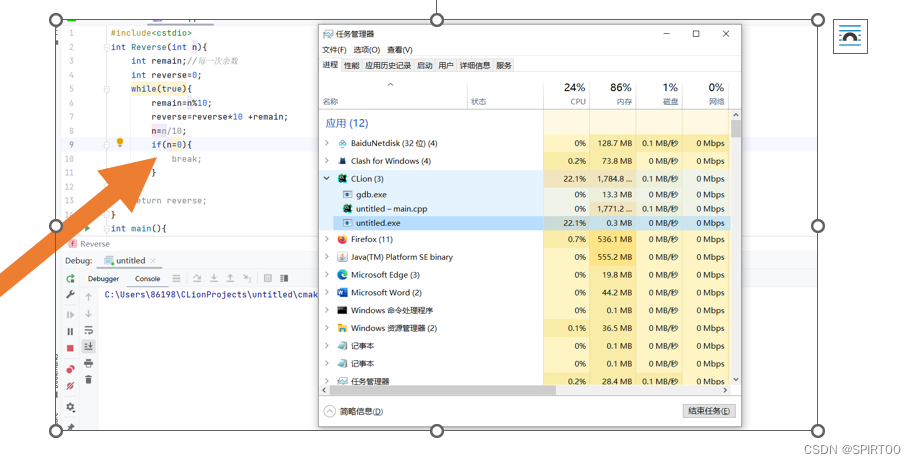
出现这种情况说明是死循环,占用很大的cpu。
如果解决:可用任务管理器查看
出现死循环时,检查入口,break的地方。
c语言中0代表假,也可打开断点进行调试。
编程规范1. if(0==n){}不省略{}
总结
人生的意义于我而言在于追求卓越。

之解耦方法论:如何通过封装、抽象、模块化、中间层等解耦代码?)


![[晓丽紫]每日论文分享(有中文摘要,源码或项目地址)--大模型,扩散模型...](http://pic.xiahunao.cn/[晓丽紫]每日论文分享(有中文摘要,源码或项目地址)--大模型,扩散模型...)


应用,FOR循环,解决存储表内存溢出的问题)


)

)
)
)



主从复制)
