当前版本:
- Python 3.8.4
简介
Python中的集合是一种无序、可哈希的且不重复的数据类型,用于存储唯一的元素。集合的实现基于哈希表,因此在插入、查找和删除元素时具有高效性能。集合的每个元素都必须是不可变的,可以是数字、字符串、元组等。
文章目录如下
1. 如何定义集合
集合都有哪些特点呢?
集合的定义方法
2. 集合的操作
2.1. 添加元素
2.2. 删除元素
2.3. 修改元素
2.4. 访问元素
2.5. 统计元素
2.6. 成员检查
3. 集合的运算
3.1. 并集运算
3.2. 交集运算
3.3. 差集运算
3.4. 对称差集
1. 如何定义集合
在python中,一般通过花括号或set来定义一个集合,例如
S = set() # 定义一个空的集合使用花括号定义一个有数据的集合
S = {1}注意:由于定义集合的符号与字典一致,所以当定义一个空的花括号会被识别为字典,而不是集合

集合都有哪些特点呢?
- 集合中的元素是唯一的,重复的元素会被自动忽略。
- 集合是无序的,元素没有固定的位置。
- 集合中的元素必须是可哈希的,因此,只能包含不可变对象,如数字、字符串、元组等。
- 集合支持常用的集合操作,如并集、交集、差集等。
集合的定义方法
我们一般使用花括号来定义一个集合,当集合中存在多个数据时,使用逗号将其分割,而这些数据被称为元素。
S = {"元素1", "元素2", "元素3"}这些元素可以是数字、字符串、元组等
S = {1.1, "AA", ("X", "Y")}
由于集合中的元素必须是可哈希的(hashable)。
- 可哈希的对象是指在其生命周期内其哈希值不变的对象,例如数字、字符串、元组等。
如列表、字典是不可哈希的对象(指在其生命周期中可能发生变化的对象)是无法定义到集合中
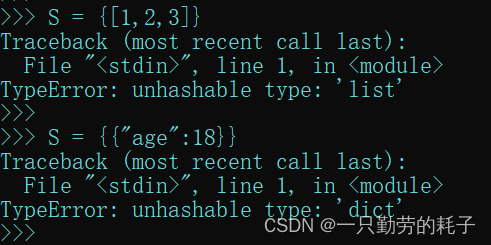
虽然不能定义到集合中,但是可以将列表转换为集合
L = [1, 2, 3]
S = set(L)
由于集合其中一个特性是不可重复,这也就意味着将某个列表元素去重时,可以利用集合来实现。
# 定义一个列表
L = ["AAA", 10, "AAA", 20, "BBB"]# 将列表转换为集合(自动去重)
S = set(L)# 再将集合转换为列表
L = list(S)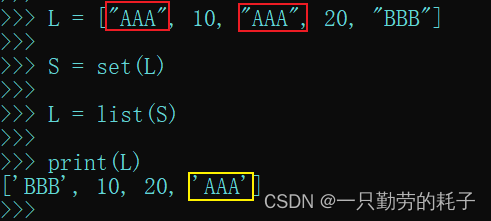
2. 集合的操作
理解了集合的特性,以及定义的方式,下面介绍一些集合的常见用法:增删改查、统计、判断等。
2.1. 添加元素
常用的两种添加元素方法:
- add:向集合中添加一个元素。如果集合中已经存在该元素,则不会进行任何操作。
- update:向集合中添加一个或多个元素,参数可以是可迭代对象。
【案例一】添加一个元素 add
S = {"A", "B"}
S.add(10)
【案例二】添加多个元素 update
S = {"A", "B"}
S.update([1, 2, 3])
2.2. 删除元素
常见有4种删除元素的方法:
- remove:如果元素在集合中,则移除该元素,否则会引发 KeyError 错误。
- discard:如果元素在集合中,则移除该元素,否则不做任何操作。
- pop:随机移除并返回集合中的一个元素。如果集合为空,会引发 KeyError 错误。
- clear:移除集合中所有的元素
【案例一】移除一个元素,若不存在则引发错误 remove
S = {"A", "B", "C"}
S.remove("A")
【案例二】移除一个元素,若不存在则不做任何操作 discard
S = {"A", "B", "C"}
S.discard("A")
【案例三】随机移除一个元素,若集合为空则报错 pop
S = {"A", "B", "C"}
S.pop()
【案例四】清空元素 clear
S = {"A", "B", "C"}
S.clear()
2.3. 修改元素
集合是无序且不可更改的,所以需要修改某个元素时只能先删除,后添加
S = {"A", "B", "C"}# 移除B
S.discard("B")# 添加E
S.add("E")
2.4. 访问元素
由于集合是无序的,所以在需要使用索引来访问某个元素时,可以将其转换为列表后操作。但问题又来了,虽然可以使用列表访问,但顺序已经被打乱后是无法精确匹配某个元素的,这对我们来说毫无意义。
集合一般是用于存储唯一元素的无序数据结构,重点在于元素的唯一性和高效的成员关系测试。所以它的重点并不是用于访问单个元素,而是用于快速读取。
S = {1, 2, "A", "B"}
for i in S:print(f"当前元素是: {i}")
2.5. 统计元素
这一章节主要介绍统计元素的个数、以及求最大值、最小值等
【案例一】统计元素个数 len
S = {1, 2, "A", "B"}
len(S)
【案例二】求最大值(仅全数字)max
S = {1.2, 5, 0.8, 6}
max(S)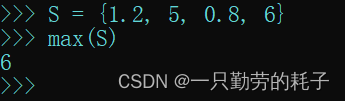
【案例三】求最小值(仅全数字)min
S = {1.2, 5, 0.8, 6}
min(S)
【案例四】求和(仅全数字)sum
S = {1.2, 5, 0.8, 6}
sum(S)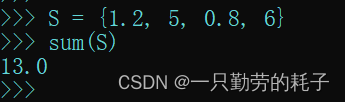
【案例五】求平均值(仅全数字)sum/len
S = {1.2, 5, 0.8, 6}
sum(S) / len(S)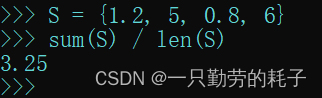
2.6. 成员检查
- 集合提供了一种高效的方法来检查元素是否属于某个集合。使用集合的成员关系操作,可以快速判断一个元素是否在集合中。
在集合中一般通过 in 判断某个元素是否存在。成功为True,失败为False
S = {1, 2, "A", "B"}
"A" in S
"A" not in S
3. 集合的运算
集合可以进行并集、交集、差集、对称差集等运算,用于解决各种集合操作问题。
3.1. 并集运算
并集是指将两个或多个集合中的所有元素合并成一个新的集合的操作。在数学符号中,通常用符号∪(并集符号)表示。在集合中使用符号 | 或者 union() 方法来实现。
- 当两个集合中存在相同的元素时将被合并成1个。
【案例一】| 符号实现并集
S1 = {1, 2, 3}
S2 = {3, 4, 5}
union_set = S1 | S2
【案例二】union() 实现并集
S1 = {1, 2, 3}
S2 = {3, 4, 5}
union_set = S1.union(S2)
3.2. 交集运算
交集是指两个集合中共同存在的元素所构成的新集合。在数学符号中,通常用符号∩(交集符号)表示。在集合中使用符号 & 或者 intersection() 方法来实现。
【案例一】& 符号实现交集
S1 = {1, 2, 3}
S2 = {3, 4, 5}
intersection_set = S1 & S2
【案例二】intersection() 实现交集
S1 = {1, 2, 3}
S2 = {3, 4, 5}
intersection_set = S1.intersection(S2)
3.3. 差集运算
差集是指一个集合相对于另一个集合的差异部分所构成的新集合。在数学符号中,通常使用符号 (-(减号)) 或者 (-(差集符号)) 表示。在集合中使用符号 - 或者 difference() 方法来实现。
【案例一】符号 - 实现差集
S1 = {1, 2, 3, 4, 5}
S2 = {3, 4, 5}
difference_set = S1 - S2
【案例二】difference() 实现差集
S1 = {1, 2, 3, 4, 5}
S2 = {3, 4, 5}
difference_set = S1.difference(S2)
【案例三】被 - 集合存在不同的元素
S1 = {1, 2, 3, 4, 5}
S2 = {3, 4, 5, 6}
difference_set = S1 - S2
3.4. 对称差集
对称差集用于表示两个集合之间的差异,包含的是那些只属于其中一个集合的元素,而不属于两个集合的交集。
【案例一】符号 ^ 实现对称差集
S1 = {1, 2, 3}
S2 = {2, 3, 4}
symmetric_difference = S1 ^ S2
【案例二】symmetric_difference() 实现对称差集
S1 = {1, 2, 3}
S2 = {2, 3, 4}
symmetric_difference = S1.symmetric_difference(S2)
异常日志)


)



)


)


)

)



