掩模数组M在卷积中的使用方式有三个有趣的属性。首先，M阵列的大小通常很小。大多数卷积掩模在每个维度上都少于10个元素。即使在3D卷积的情况下，掩码通常也只包含少于1000个元素。其次，在内核执行过程中，M的内容不会改变。第三，所有线程都需要访问掩码元素。更好的是，所有线程都以相同的顺序访问M元素，从M[0]开始，并通过图7.6.中for循环的迭代一次移动一个元素。这两个属性使掩码数组成为恒定内存和缓存的绝佳候选（图7.7）。

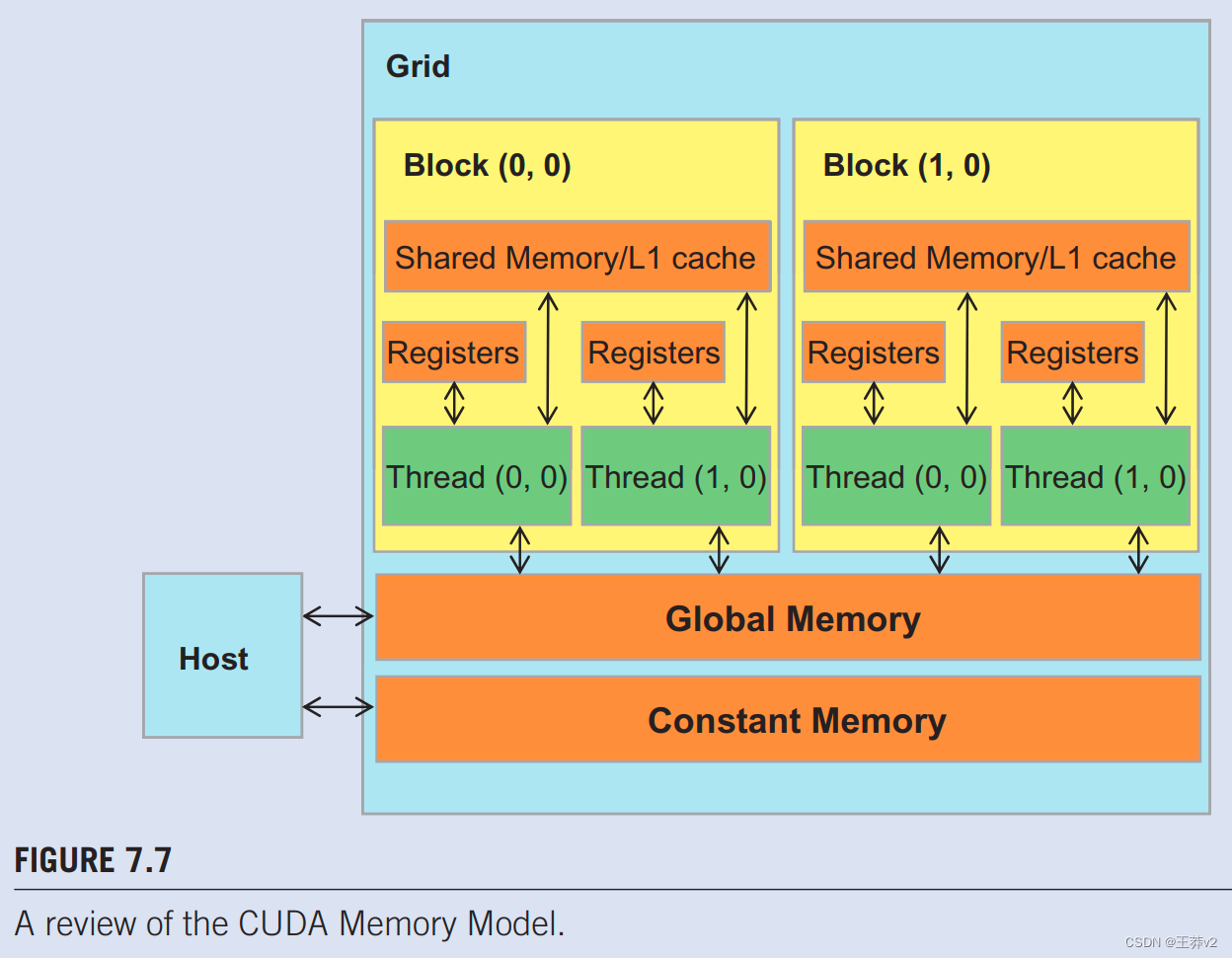
正如我们在第5章（性能考虑因素）中讨论的那样，CUDA编程模型允许程序员在常量内存中声明一个变量。与全局内存变量一样，常量内存变量对所有线程块也是可见的。主要区别在于，在内核执行期间，线程不能更改常量内存变量。此外，恒定内存的大小相当小，目前为64KB。

为了使用常量内存，主机代码需要以与全局内存变量不同的方式分配和复制常量内存变量。要在常量内存中声明M数组，主机代码将其声明为全局变量，如下所示：

#define MAX_MASK_WIDTH 10
__constant__ float M[MAX_MASK_WIDTH];

这是一个全局变量声明，应该在源文件中的任何函数之外。关键字__constant__（每边两个下划线）告诉编译器，数组M应放入设备常量内存中。

假设主机代码已经在带有Mask_Width元素的主机内存中的掩码M_h数组中分配并初始化了掩码。M_h的内容可以在设备常量存储器中传输到M，如下所示：

请注意，这是一个特殊的内存复制函数，它通知CUDA运行时，在内核执行期间，复制到常量内存的数据不会更改。一般来说，cudaMemcpyToSymble（）函数的使用如下：
其中dest是指向常量内存中目标位置的指针，src是指向主机内存中源数据的指针，大小是要复制的字节数。

内核函数作为全局变量访问常量内存变量。因此，它们的指针不需要作为参数传递给内核。我们可以修改内核以使用常量内存，如图7.8.所示。请注意，内核看起来与图7.6.中几乎相同。唯一的区别是，M不再通过作为参数传入的指针访问。它现在作为主机代码声明的全局变量进行访问。请记住，全局变量的所有C语言范围规则都适用于这里。如果hostl代码和内核代码在不同的文件中，内核代码文件必须包含相关的外部声明信息，以确保M的声明对内核可见。

与全局内存变量一样，恒定内存变量也位于DRAM中。然而，由于CUDA运行时知道常量内存变量在内核执行期间不会被修改，它指示硬件在内核执行期间积极缓存常量内存变量。为了了解恒定内存使用的好处，我们首先需要更多地了解现代处理器内存和缓存层次结构。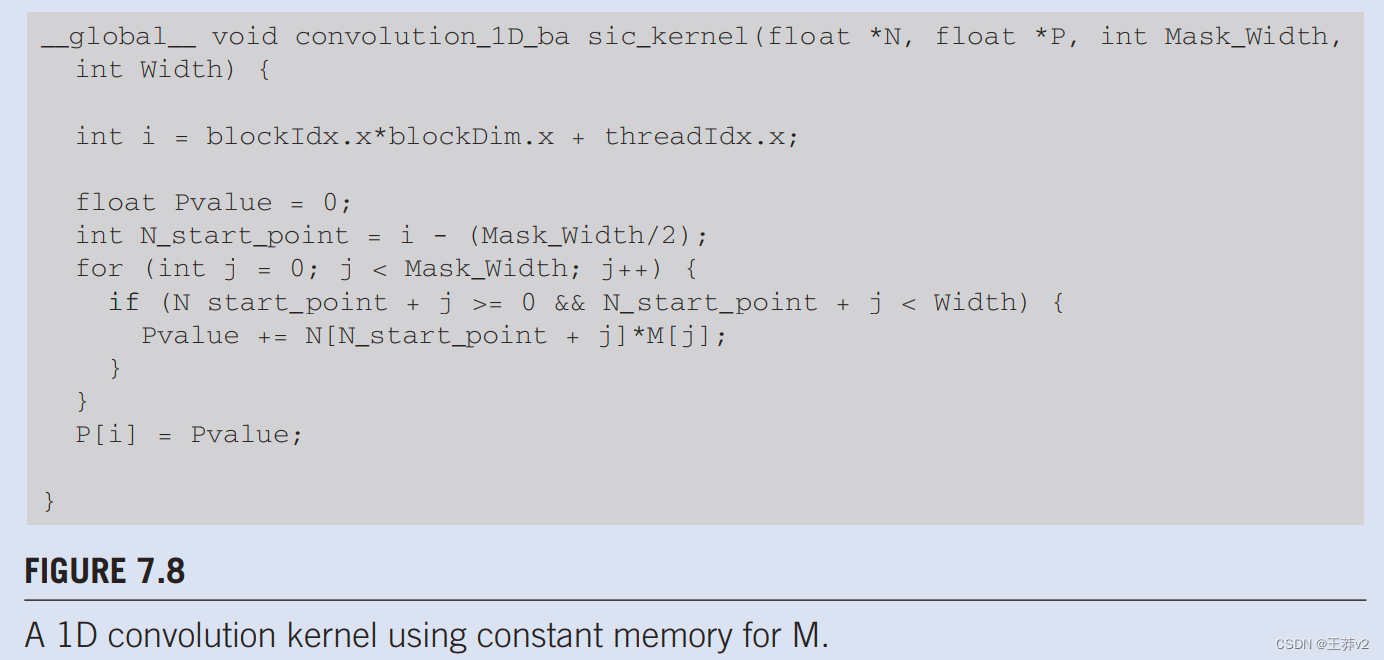
正如我们在第5章中讨论的，性能考虑，DRAM的长延迟和有限的带宽几乎是所有现代处理器的主要瓶颈。为了减轻内存瓶颈的影响，现代处理器通常使用片上缓存存储器或缓存，以减少需要从主存储器（DRAM）访问的变量数量，如图7.9所示。

与CUDA共享内存或一般的暂存不同，缓存对程序是“透明”的。也就是说，为了使用CUDA共享内存，程序需要将变量声明为__shared_ _，并显式地将全局内存变量移动到共享内存变量中。另一方面，在使用缓存时，程序只需访问原始变量。处理器硬件将自动在缓存中保留一些最近或最常用的变量，并记住其原始DRAM地址。当稍后使用其中一个保留的变量时，硬件将从其地址中检测出该变量的副本在缓存中可用。然后，变量的值将从缓存中提供，无需访问DRAM。

内存的大小和内存的速度之间存在权衡。因此，现代处理器通常使用多个级别的缓存。这些缓存级别的编号约定反映了与处理器的距离。最低级别，L1或1级，是直接连接到处理器核心的缓存。它在延迟和带宽方面都以非常接近处理器的速度运行。然而，L1缓存体积较小，通常在16KB到64KB之间。L2缓存更大，范围在128KB到1MB之间，但可能需要数十个周期才能访问。它们通常在多个处理器内核或CUDA设备中的SM之间共享。在今天的一些高端处理器中，甚至有L3缓存，大小可以为几MB。

在大规模并行处理器中使用缓存的一个主要设计问题是缓存一致性，当一个或多个处理器内核修改缓存数据时，就会出现缓存一致性。由于L1缓存通常只直接连接到其中一个处理器内核，因此其他处理器内核不容易观察到其内容的变化。如果修改后的变量在不同处理器内核上运行的线程之间共享，这会导致问题。需要一个缓存一致性机制，以确保其他处理器内核的缓存内容得到更新。在大规模并行处理器中提供缓存一致性既困难又昂贵。然而，它们的存在通常简化了并行软件开发。因此，现代CPU通常支持处理器内核之间的缓存一致性。虽然现代GPU提供两级缓存，但它们通常没有缓存一致性，以最大限度地利用可用的硬件资源，以增加处理器的算术吞吐量。

恒定内存变量在大规模并行处理器中使用缓存中起着有趣的作用。由于它们在内核执行期间没有更改，因此在内核执行期间没有缓存一致性问题。因此，硬件可以积极缓存L1缓存中的常量变量值。此外，这些处理器中的缓存设计通常经过优化，以向大量线程广播值。因此，当warp中的所有线程访问相同的恒定内存变量时，就像M的情况一样，缓存可以提供大量的带宽来满足线程的数据需求。此外，由于M的大小通常很小，我们可以假设所有M元素都有效地从缓存中访问。因此，我们可以简单地假设**没有在M访问上花费DRAM带宽。**通过使用恒定内存和缓存，我们有效地将浮点算术与内存访问的比率增加了一倍，达到2。

事实证明，对输入N阵列元素的访问也可以从较新的GPU中的缓存中受益。我们将在第7.5节中回到这一点。