51. N皇后
题目
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:

- 输入:n = 4
- 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
思考
看到题就懵了,感觉和之前做的回溯算法完全不一样,这是真的开放性的题,开了卡哥的视频大概梳理出来了一些思路:
1、要创建的结果数组是三维的,因为棋盘是二维的,要存放棋盘
2、因为棋盘是n*n的,那么当纵向递归遍历到n时,收获结果
3、单层递归其实没啥难度,主要是判断当满足题意三个条件时才能纵向递归,注意这里要因为是在二维数组里递归,那么横向遍历的i和纵向递归遍历其实没啥关系,不用startIndex,直接row+1即可
4、满足的三个条件怎么写:
- 不能同一列出现两个Q,即col不变,判断从0到row的所有数是否有Q
- 不能45度出现Q,即3,3到2,2到1,1或者3,2到2,1不能出出现Q,row-1,col-1即可
- 不能135度出现Q,出3,3到2,4到1,5不能出现Q,row-1,col+1即可
代码
class Solution {
public:
vector<vector<string>> res;
void backTracking(vector<string>& chess, int n, int row){
if(row == n) {
res.push_back(chess);
return;
}
for(int col = 0; col < n; col++) {
if(isValid(row, col, chess, n)){
chess[row][col] = 'Q';
backTracking(chess, n, row+1);
chess[row][col] = '.';
}
}
}
bool isValid(int row, int col, vector<string> chess, int n ) {
for(int i = 0; i < row; i++) {
if(chess[i][col] == 'Q') return false;
}
for(int i = row-1, j = col-1; i>=0 && j>=0; i--&j--) {
if(chess[i][j]== 'Q') return false;
}
for(int i = row -1, j = col+1; i>=0 && j<n; i-- && j++) {
if(chess[i][j] == 'Q') return false;
}
return true;
}
vector<vector<string>> solveNQueens(int n) {
vector<string> chess(n, string(n, '.'));
backTracking(chess, n, 0);
return res;
}
};
37. 解数独
题目
编写一个程序,通过填充空格来解决数独问题。
一个数独的解法需遵循如下规则: 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。 空白格用 '.' 表示。

一个数独。
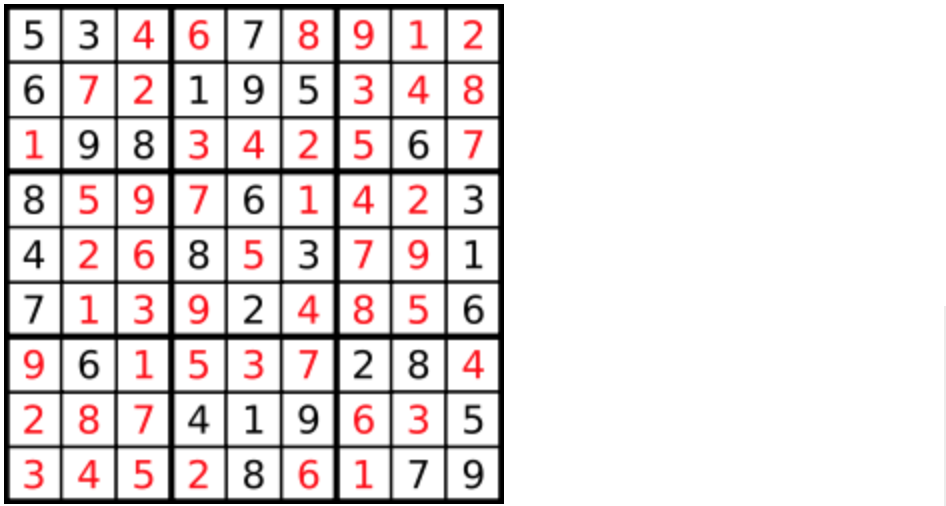
答案被标成红色。
提示:
- 给定的数独序列只包含数字 1-9 和字符 '.' 。
- 你可以假设给定的数独只有唯一解。
- 给定数独永远是 9x9 形式的。
思考
太难了,感觉和n皇后是差不多的,也是三个条件,但是具体应该怎么写完全一头雾水,看完卡哥视频稍微总结一下吧:
- 上来不是void函数,是bool类型的,直接遍历,i<9,j<9
- 当board[i][j] =='.'时,说明需要填充数字,开始循环判断1-9中哪个数字满足条件,如果满足,直接填上
- 注意,这里的中止条件竟然在填充完数字后,如果填充了,那么判断整个函数是否为true,如果为true,返回true
- 如果1-9中数字不满足条件,那么要return false
- 三个条件写法
- 纵向判断要填充的数字是否已经在那一列里
- 横向判断要填充的数字是否已经在那一行里
- 在3*3的九宫格里判断要填充的数字是否在九宫格里,用两个for循环,并且startRow和StartCol需要用(row/3)*3来表示
代码
class Solution {
private:
bool backTracking(vector<vector<char>>& board) {
for(int i = 0; i < board.size(); i++) {
for(int j = 0; j < board.size(); j++) {
if(board[i][j] == '.') {
for(char k = '1'; k <= '9'; k++) {
if(isValid(i, j, k, board)) {
board[i][j] = k;
bool tmp = backTracking(board);
if(tmp) return true;
board[i][j] = '.';
}
}
return false;
}
}
}
return true;
}
bool isValid(int row, int col, char val, vector<vector<char>>& board) {
for(int i = 0; i < 9; i++) {
if(board[row][i] == val) return false;
}
for(int j = 0; j < 9; j++) {
if(board[j][col] == val) return false;
}
int startRow = (row/3) * 3;
int startCol = (col/3) * 3;
for(int i = startRow; i < startRow+3; i++) {
for(int j = startCol; j < startCol+3; j++) {
if(board[i][j] == val) return false;
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
backTracking(board);
}
};


)




线性回归算法和多元线性回归)








 锁)


