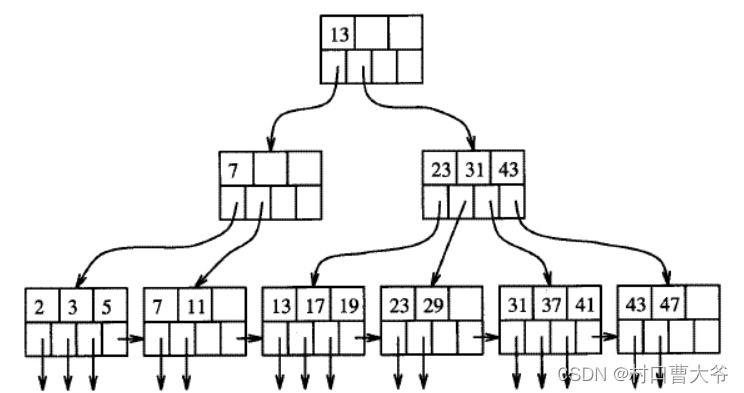
概述:B 树(B-tree)是一种自平衡的搜索树数据结构,广泛应用于数据库和文件系统等领域。它的设计旨在提供一种高效的插入、删除和查找操作,同时保持树的平衡,确保各个节点的深度相差不大。
B 树的特点包括:
-
平衡性: 所有叶子节点到根节点的路径长度相等,确保在查找、插入和删除等操作时,各个节点的访问次数相对均衡,提高了性能。
-
多路搜索: B 树每个内部节点可以有多个子节点,这是与二叉搜索树的主要区别。每个节点包含多个关键字和对应的子树,这样可以减少树的高度,提高检索效率。
-
节点存储多个关键字: 每个节点可以存储多个关键字,而不仅仅是一个。这样可以提高每个节点的利用率,减少磁盘 I/O 次数。
-
自调整: 在插入和删除操作时,B 树会自动调整其结构以保持平衡。这通过节点分裂和合并的方式来实现。
B 树的阶数(order)是一个重要的概念,它表示一个节点最多可以包含的子节点数(或关键字数)。通常,B 树的阶数会根据具体的使用场景进行调整,以满足性能和空间的需求。
B 树广泛应用于数据库系统中,作为索引结构,因为它能够高效地支持范围查询、插入和删除操作。同时,B 树也被用于文件系统,以加速文件的检索和访问。
完整代码:
#include <stdio.h>
#include <stdlib.h>// B 树的阶数
#define ORDER 3// B 树节点结构
typedef struct BTreeNode {int leaf; // 是否是叶子节点int n; // 当前关键字数量int keys[ORDER - 1]; // 关键字数组struct BTreeNode* child[ORDER]; // 子节点数组
} BTreeNode;// 创建新节点
BTreeNode* createNode() {BTreeNode* newNode = (BTreeNode*)malloc(sizeof(BTreeNode));newNode->leaf = 1;newNode->n = 0;for (int i = 0; i < ORDER - 1; ++i) {newNode->keys[i] = 0;}for (int i = 0; i < ORDER; ++i) {newNode->child[i] = NULL;}return newNode;
}// 分裂节点
void splitChild(BTreeNode* parent, int index, BTreeNode* child) {BTreeNode* newNode = createNode();newNode->leaf = child->leaf;newNode->n = ORDER / 2 - 1;// 将 child 中的一半关键字移动到 newNode 中for (int i = 0; i < ORDER / 2 - 1; ++i) {newNode->keys[i] = child->keys[i + ORDER / 2];}// 如果 child 不是叶子节点,将一半子节点移动到 newNode 中if (!child->leaf) {for (int i = 0; i < ORDER / 2; ++i) {newNode->child[i] = child->child[i + ORDER / 2];child->child[i + ORDER / 2] = NULL;}}// 调整 child 的关键字数量child->n = ORDER / 2 - 1;newNode->n = ORDER / 2 - 1;// 将 parent 中的一个关键字和 newNode 相关的子节点插入到 parent 中for (int i = parent->n; i > index; --i) {parent->keys[i] = parent->keys[i - 1];parent->child[i + 1] = parent->child[i];}parent->keys[index] = child->keys[ORDER / 2 - 1];parent->child[index + 1] = newNode;// 调整 parent 的关键字数量parent->n++;// 将 parent 中的一个关键字插入到 child 中child->keys[ORDER / 2 - 1] = 0;child->child[ORDER / 2] = NULL;
}// 插入非满节点
void insertNonFull(BTreeNode** root, int key) {BTreeNode* node = *root;int i = node->n - 1;// 如果是叶子节点,直接插入if (node->leaf) {while (i >= 0 && key < node->keys[i]) {node->keys[i + 1] = node->keys[i];i--;}node->keys[i + 1] = key;node->n++;} else {// 如果是内部节点,找到要插入的子节点while (i >= 0 && key < node->keys[i]) {i--;}i++;// 如果子节点已满,先分裂再插入if (node->child[i]->n == ORDER - 1) {splitChild(node, i, node->child[i]);if (key > node->keys[i]) {i++;}}// 递归插入子节点insertNonFull(&(node->child[i]), key);}
}// 插入关键字
void insert(BTreeNode** root, int key) {BTreeNode* node = *root;// 如果树为空,创建一个新节点作为根if (!node) {*root = createNode();(*root)->keys[0] = key;(*root)->n = 1;return;}// 如果根节点已满,先分裂再插入if (node->n == ORDER - 1) {BTreeNode* newRoot = createNode();newRoot->leaf = 0;newRoot->child[0] = *root;*root = newRoot;splitChild(newRoot, 0, node);insertNonFull(root, key);} else {insertNonFull(root, key);}
}// 打印 B 树
void printBTree(BTreeNode* node, int level) {if (node) {printf("Level %d: ", level);for (int i = 0; i < node->n; ++i) {printf("%d ", node->keys[i]);}printf("\n");if (!node->leaf) {for (int i = 0; i <= node->n; ++i) {printBTree(node->child[i], level + 1);}}}
}int main() {BTreeNode* root = NULL;// 插入一些关键字insert(&root, 3);insert(&root, 7);insert(&root, 2);insert(&root, 9);insert(&root, 1);insert(&root, 6);insert(&root, 4);insert(&root, 5);insert(&root, 8);// 打印 B 树printBTree(root, 0);return 0;
}首先定义了B树的阶数ORDER为3,即每个节点最多可以有3个子节点。然后定义了一个B树节点的结构体,包含以下成员:
- leaf:表示该节点是否为叶子节点,如果是叶子节点则为1,否则为0。
- n:表示当前节点中关键字的数量。
- keys:关键字数组,用于存储节点中的关键字。
- child:子节点数组,用于存储指向子节点的指针。
接下来实现了创建新节点的函数createNode(),用于分配内存并初始化节点的成员变量。
然后实现了分裂节点的函数splitChild(),用于将一个节点分裂成两个节点。分裂过程包括将原节点的一半关键字移动到新节点中,并将原节点的一半子节点移动到新节点中。同时调整原节点的关键字数量和新节点的关键字数量。最后将原节点中的一个关键字和与新节点相关的子节点插入到原节点中,并调整原节点的关键字数量。
接着实现了插入非满节点的函数insertNonFull(),用于在非满节点中插入关键字。如果节点是叶子节点,则直接插入关键字;如果节点是内部节点,则找到要插入的子节点,如果子节点已满,则先分裂再插入。然后递归插入子节点。
最后实现了插入关键字的函数insert(),用于向B树中插入关键字。如果树为空,则创建一个新节点作为根;如果根节点已满,则先分裂再插入。然后调用insertNonFull()函数插入关键字。
最后实现了打印B树的函数printBTree(),用于按层次遍历的方式打印B树的结构。
在main()函数中,创建了一个空的根节点root,然后插入了一些关键字,并调用printBTree()函数打印B树的结构。

)

)



:环境配置)


)







DOM)