数据结构：堆和堆排序

1.二叉树的存储结构

1.顺序结构

顺序结构存储就是使用数组来表示一棵二叉树，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实使用中只有堆才会使用数组来存储。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。

2.链式结构

二叉树的链式存储是使用链表来表示一棵二叉树，即用指针链接来指示元素的逻辑关系。 通常的方法是
链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所
在的链结点的存储地址 。

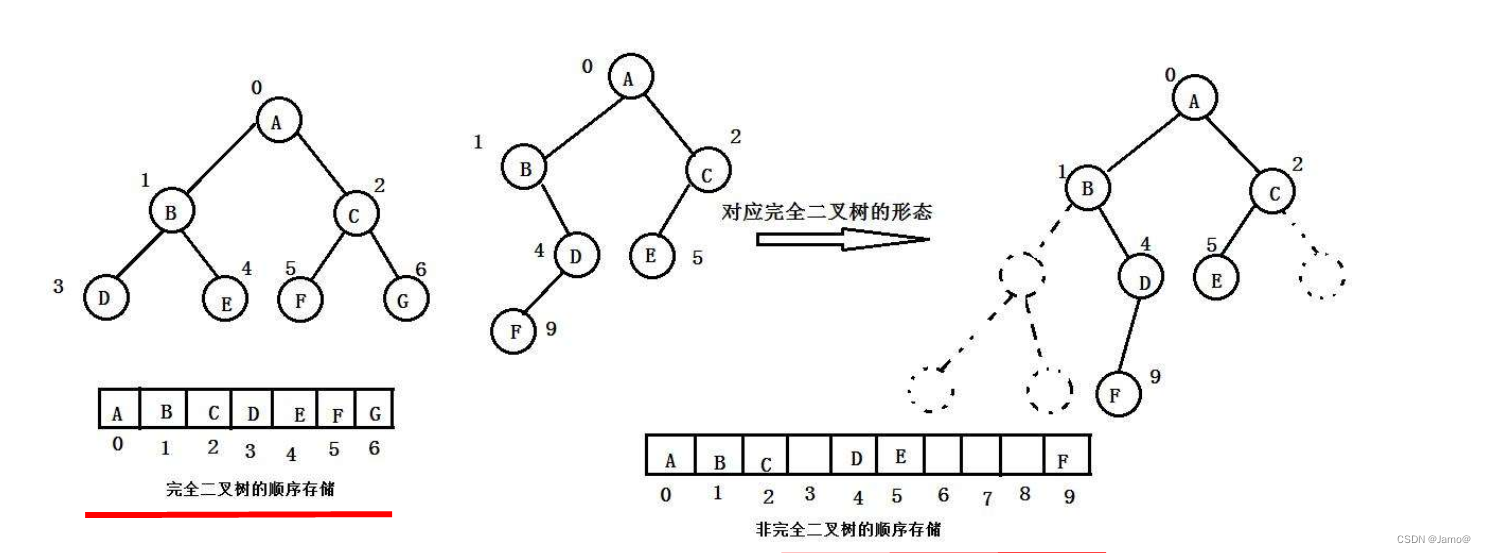
2.堆

堆实际上就是一棵完全二叉树：

其性质为：

• 堆中某个节点的值总是不大于或不小于其父节点的值；
• 堆总是一棵完全二叉树。

大堆和小堆：

• 每个节点的值都大于或等于其子节点的值，为大堆；反之为小堆。

3.堆的实现

#define _CRT_SECURE_NO_WARNINGS 1#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include<stdbool.h>
// （大小）堆的实现（堆的结构与特点发现与数组下标有紧密关系）因此可以使用顺序表结构体
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}Heap;// 堆的构建
void HeapCreate(Heap* hp);// 堆的销毁
void HeapDestory(Heap* hp);
// 向上调整
void AdjustUp(HPDataType* a, size_t childposition);// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 向下调整
void AdjustDown(HPDataType* a, int size, size_t parentposition);// 堆的删除
void HeapPop(Heap* hp);// 取堆顶的数据
HPDataType HeapTop(Heap* hp);// 堆的数据个数
int HeapSize(Heap* hp);// 堆的判空
bool HeapEmpty(Heap* hp);

---

#include "Heap.h"// 堆的构建
void HeapCreate(Heap* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}
// 堆的销毁
void HeapDestory(Heap* hp)
{free(hp->a);hp->capacity = 0;hp->size = 0;hp = NULL;
}
// 向上调整
void AdjustUp(HPDataType* a, size_t childposition)
{assert(a);size_t parentposition = (childposition - 1) / 2;while (childposition > 0){// 小堆if (a[childposition] < a[parentposition]){// 交换孩子和父亲的值HPDataType  tmp = a[childposition];a[childposition] = a[parentposition];a[parentposition] = tmp;childposition = parentposition;parentposition = (parentposition - 1) / 2;}else{return;}}
}
// 堆的插入
void HeapPush(Heap* hp, HPDataType x)
{assert(hp);// 检查容量if (hp->size == hp->capacity){int newcapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;HPDataType* newa = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newcapacity);if (newa == NULL){perror("realloc fail");return;}hp->a = newa;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;// 向上调整(可用递归可用循环，此处我们用循环实现)AdjustUp(hp->a, hp->size - 1);}
// 向下调整
void AdjustDown(HPDataType* a, int size, size_t parentposition)
{assert(a);size_t childposition = a[1] < a[2] ? 1 : 2;while (childposition < size){if (a[childposition] < a[parentposition])// 小堆{HPDataType tmp = a[childposition];a[childposition] = a[parentposition];a[parentposition] = tmp;parentposition = childposition;childposition = a[childposition * 2 + 1] < a[childposition * 2 + 2] ? childposition * 2 + 1 : childposition * 2 + 2;}else{break;}}
}// 堆的删除(删除堆顶元素)
void HeapPop(Heap* hp)
{assert(hp);if (hp->size == 0){printf("堆为空，无法删除\n");return;}HPDataType tmp = hp->a[0];hp->a[0] = hp->a[hp->size - 1];hp->size--;AdjustDown(hp->a, hp->size, 0);}
// 取堆顶的数据
HPDataType HeapTop(Heap* hp)
{assert(hp);return hp->a[0];
}
// 堆的数据个数
int HeapSize(Heap* hp)
{assert(hp);return hp->size;
}
// 堆的判空
bool HeapEmpty(Heap* hp)
{assert(hp);if (hp->size == 0){return true;}else{return false;}
}

4.堆排序（选择排序中的一类）

看到堆排序我们会想到是不是利用我们自己造轮子写出来的堆这个数据结构和接口函数来实现排序呢？

假设我们要对一个数组里的元素进行排序，我们可能想到这样做：

1. 将数组里的元素通通插入到堆中，插入进去的元素自然就形成了一种排序结构。
2. 再将堆里的数据取出来放回到原数组中从而进行排序。

弊端：这样进行‘’堆排序‘’实际上是十分复杂和浪费空间和时间的，这个方法前提下我们必须要先自己实现一个堆，再然后堆的构建也是要开辟内存空间的十分低效。

一次建堆的时间的复杂度是(向上调整建堆和向下调整建堆):
$$O(N\ast {\log }_{}N)$$

---

实际的堆排序：

记忆：升序建大堆，降序建小堆。

1. 基本思想

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。

① 将待排序的序列构造成一个==最大堆==，此时序列的最大值为根节点。
② 依次将根节点与待排序序列的最后一个元素交换。
③ 再维护从根节点到该元素的前一个节点为最大堆，**如此往复，最终得到一个递增序列**。

2.代码实现

// 向上调整
void AdjustUp(int* a, size_t childposition)
{assert(a);size_t parentposition = (childposition - 1) / 2;while (childposition > 0){// 大堆if (a[childposition] > a[parentposition]){// 交换孩子和父亲的值int  tmp = a[childposition];a[childposition] = a[parentposition];a[parentposition] = tmp;childposition = parentposition;parentposition = (parentposition - 1) / 2;}else{return;}}
}void swap(int* start, int* end)
{int tmp = 0;tmp = *start;*start = *end;*end = tmp;
}// 堆排序
void HeapSort(int* a, int n)
{int i = 0;// 当数据个数大于1时才进行排序，否则直接就是有序的while (n > 1){// 建大堆使得最大的数位于堆顶部for (i = 1; i < n; i++){AdjustUp(a, i);}// 堆顶元素与堆最后一个元素交换位置swap(&a[0], &a[n - 1]);// 除去堆最后一个位置的元素重新建立大堆，如此往复，最终得到一个递增序列n--;}
}

---

#define  _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>void HeapSort(int* a, int n);
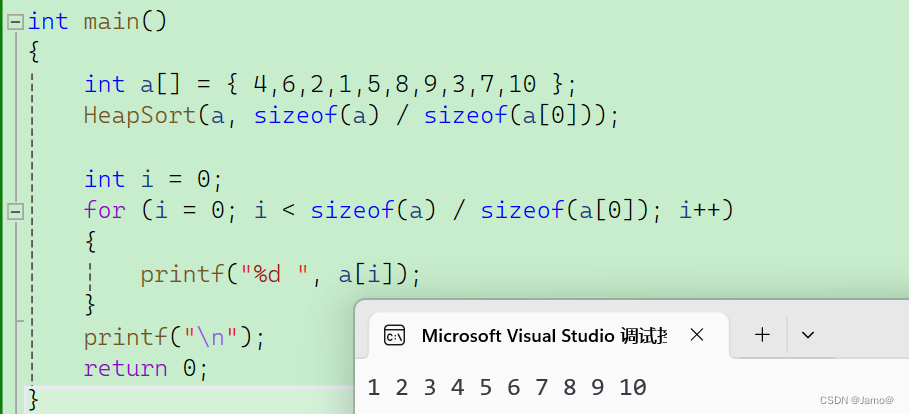
void AdjustUp(int* a, size_t childposition);int main()
{int a[] = { 4,6,2,1,5,8,9,3,7,10 };HeapSort(a, sizeof(a) / sizeof(a[0]));int i = 0;for (i = 0; i < sizeof(a) / sizeof(a[0]); i++){printf("%d ", a[i]);}printf("\n");return 0;
}