---

前言

参考视频：数据结构与算法基础（青岛大学-王卓）
KMP算法之求next数组代码讲解

一、串

回忆一下 之前学习的线性结构元素都是一一对应的关系。
栈和队列是操作受限的线性表
字符串依然是线性结构
不过和前面学习的顺序表，栈，队列，有一个不一样的地方，就是限定了元素：只能是字符，而顺序表，栈，队列可以有其他元素。
插一句，广义表这些可以看成是线性表的推广，但是严格意义上已经不是线性表了。

1.1、串的定义

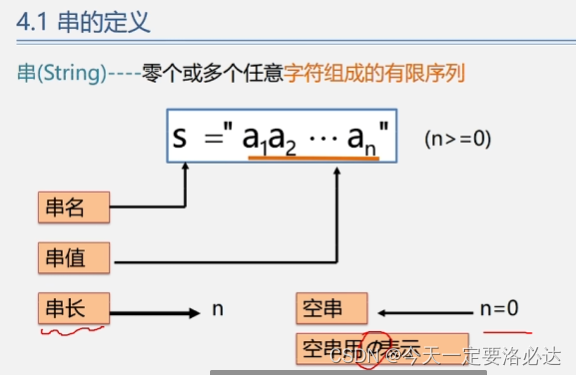
字符串的定义：零个或多个任意字符组成的有限序列
定义部分还有串名，串值，串长。串长为0时就是空串。

字串：串中任意个连续字符组成的子序列（包括空串）称为该串的字串
真子串：不包含自身的子串
注意，空串也是子串

主串：包含子串的串叫主串
字符位置：字符在序列中的序号成为该字符在串中的位置
子串位置：子串第一个字符在串中的位置
空格串：由一个或多个空格组成的串（与空串的概念不同哈）

来个PPT中的例题看看：（这里位置默认是从1开始）

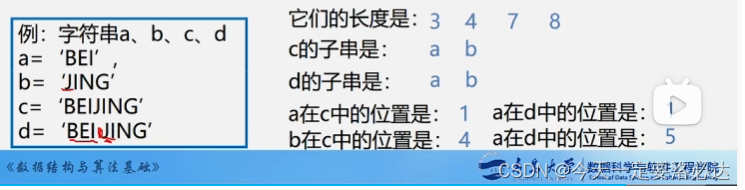
注意最后一个小问PPT里写错了：应该是b在d中的位置是5

串相等：长度相等，且各个对应位置的字符都相同，才是相等
所有的空串都是相等的

1.2、案例引入

案例一：病毒是否出现（病毒相当于就是子串，检测是否在主串中出现）


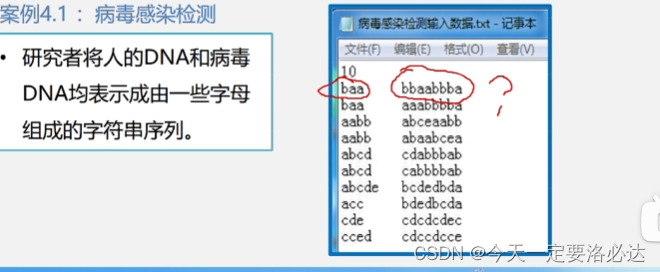
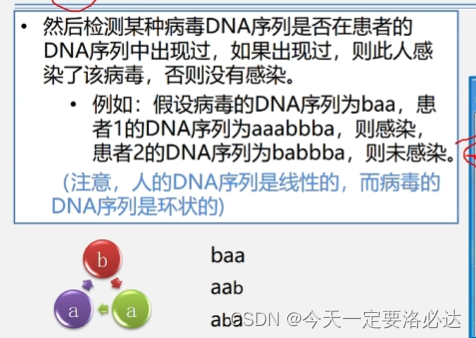
患者1看起来好像没感染，是因为忽视了病毒是环状这个前提条件
baa还可以是aab aba 这样就能匹配上了
当然像我视力比较好的情况 我一眼也看出来倒数两个字符和第一个字符组成了病毒串

这种案例引入的问题有：一个字符串是否在另外一个字符串中出现过？如果出现过，出现的位置在哪里？这就是字符串的匹配问题

1.3、串的类型定义和存储结构

字符串的数据关系依然是这种前驱后继的关系：一对一的关系

字符串依然有顺序存储结构和链式存储结构：（逻辑结构是线性结构）

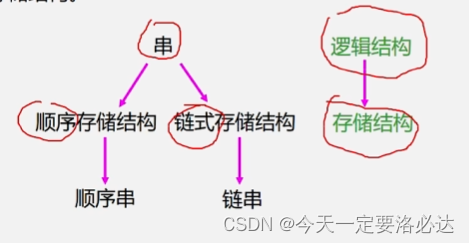
字符串的顺序存储结构：

这里字符串和前面线性表不一样的地方是：线性表定义中的元素类型没有限定死，可以是其他类型的（比如int）

字符串的链式存储结构：

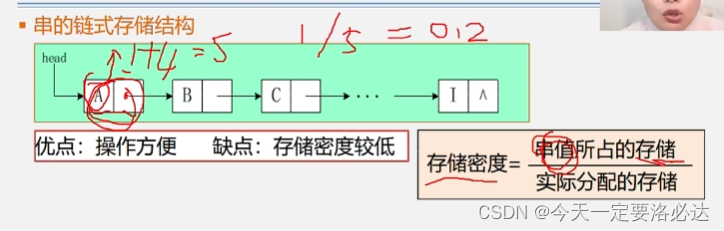
链式存储的存储密度是非常低的，对于一个结点来说，一个字符占的是1个字节，指针占4个字节（32位系统），这样存储密度就是20%。

解决方案：可以把多个字符放到同一个结点中：

对于一个结点来说，一个字符占的是1个字节，图中是4个，就是4个字节，指针占4个字节（32位系统），这样存储密度就是50%。通常称这些连在一起的字符叫做块。块中可以多放一些元素，这样存储密度就上去了。

字符串的链式存储结构常用块链结构：

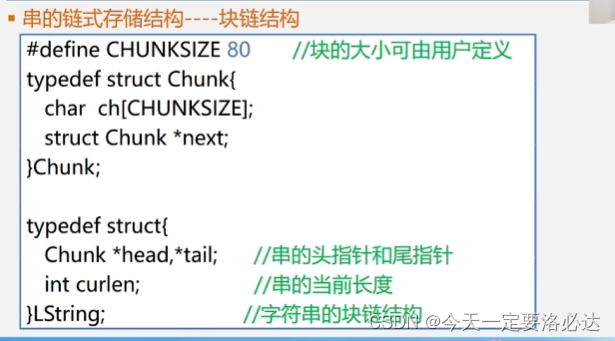
实际情况里，字符串的顺序存储我们用得更多一些，字符串中的字符插入删除比较少，更多还是匹配操作等。后面的内容也是基本围绕着顺序存储结构来的。

1.4、串的模式匹配算法

算法：确定主串中所含有的子串（模式串）第一次出现的位置（定位）
应用举例：查找某个文章里是否出现关键字

有两种经典的算法：BF和KMP

1.4.1、BF算法

称为简单匹配法。思路是穷举法
算法思路：从正文串第一个字符开始依次和模式串进行匹配。

BF算法的图解如下所示：

BF算法的C++实现：

int index_BF(SString Source,SString Target){//Source是主串，Target是子串int i,j=1;while(i<=Source.length&&j<=Target.length){if(Source.ch[i]==Target.ch[j]){//匹配成功，开始匹配下一个字符++i;++j;}else{//匹配失败，时空回溯i=i-j+2;//i-j+1+1(前面+1是因为字符串默认从1开始，没有0)j=1;//退回子串的原点}}if(j>=Target.length){return i-Target.length;}else{return 0;}
}

完整运行代码如下：

#include<iostream>
#include<string.h>
using namespace std;
#define MAXLEN 255
typedef struct{char ch[MAXLEN+1];int length;
}SString;int index_BF(SString Source,SString Target){//Source是主串，Target是子串int i,j=1;while(i<=Source.length&&j<=Target.length){if(Source.ch[i]==Target.ch[j]){//匹配成功，开始匹配下一个字符++i;++j;}else{//匹配失败，时空回溯i=i-j+2;//i-j+1+1(前面+1是因为字符串默认从1开始，没有0)j=1;//退回子串的原点}}if(j>=Target.length){return i-Target.length;}else{return 0;}
}int main(){SString mainStr, subStr;int ret;// 初始化主串cout << "请输入主串：";cin >> (mainStr.ch + 1);  // 从位置1开始存储mainStr.length = strlen(mainStr.ch + 1);// 初始化子串cout << "请输入子串：";cin >> (subStr.ch + 1);  // 从位置1开始存储subStr.length = strlen(subStr.ch + 1);ret=index_BF(mainStr,subStr);if(ret==0){cout<<"字符串匹配失败！"<<endl;}else{cout<<"字符串匹配成功，字符开始的位置是："<<ret<<endl;}
}

注意，我们这里cin >> (mainStr.ch + 1); 是从位置1开始存储，而不是位置0
我们试验一下：

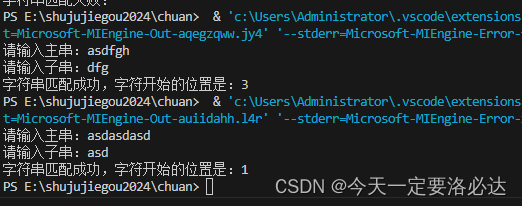
BF算法的时间复杂度：

最好情况下是比较m次（第一次比较就找到了）,为O（m）
最坏情况下是比较了（n-m+1）*m次（找到最后一组再找到，甚至没找到）,O（mn）
时间复杂度平均下来就是O（mn）/2,依然是O（mn）

1.4.2、KMP算法

KMP算法的核心就是i和j的回溯方式不同:
1)主串的指针i不需要回溯
2)模式串的指针j回溯有一套自己的规则：查看next[j]数组：next数组也就是模式串与主串“失配”时，模式串中重新和主串开始比较的初始位置。

这样能提速到O（m+n）

而里面最难的就是如何找j应该回到哪个位置，也就是求next[j]数组，以下是求它的规则：

这里的第一条规则很难懂，我也看不懂，我写了两条笔记如下，比较形象：

然后是实现KMP函数的C++代码：

void get_next(SString Target,int next[]){int i=1;int j=0;next[1]=0;while(i<=Target.length){if(j==0||Target.ch[i]==Target.ch[j]){++i;++j;next[i]=j;}else{j=next[j];}  }
}
int KMP(SString Source,SString Target,int next[]){//Source是主串，Target是子串int i=1;int j=1;while(i<=Source.length&&j<=Target.length){if(j==0||Source.ch[i]==Target.ch[j]){//匹配成功，开始匹配下一个字符++i;++j;}else{//匹配失败，查看next[j]数组进行回溯,i不用回溯j=next[j];//退回子串的原点}}if(j>=Target.length){return i-Target.length;}else{return 0;}
}

然而这里的求next数组的函数其实非常难去理解。

实现的完整代码：

#include<iostream>
#include<string.h>
using namespace std;
#define MAXLEN 255
typedef struct{char ch[MAXLEN+1];int length;
}SString;
void get_next(SString Target,int next[]){int i=1;int j=0;next[1]=0;while(i<=Target.length){if(j==0||Target.ch[i]==Target.ch[j]){++i;++j;next[i]=j;}else{j=next[j];}  }
}
int KMP(SString Source,SString Target,int next[]){//Source是主串，Target是子串int i=1;int j=1;while(i<=Source.length&&j<=Target.length){if(j==0||Source.ch[i]==Target.ch[j]){//匹配成功，开始匹配下一个字符++i;++j;}else{//匹配失败，查看next[j]数组进行回溯,i不用回溯j=next[j];//退回子串的原点}}if(j>=Target.length){return i-Target.length;}else{return 0;}
}int main(){SString mainStr, subStr;int ret;int next[1024];// 初始化主串cout << "请输入主串：";cin >> (mainStr.ch + 1);  // 从位置1开始存储mainStr.length = strlen(mainStr.ch + 1);// 初始化子串cout << "请输入子串：";cin >> (subStr.ch + 1);  // 从位置1开始存储subStr.length = strlen(subStr.ch + 1);get_next(subStr,next);ret=KMP(mainStr,subStr,next);if(ret==0){cout<<"字符串匹配失败！"<<endl;}else{cout<<"字符串匹配成功，字符开始的位置是："<<ret<<endl;}
}

二、数组

2.1、数组的定义

数组定义：按照一定格式排列起来的，具有相同类型的数据元素的集合

一位数组的定义：若线性表中的数据元素为非结构的简单元素，则为一维数组。

一维数组的逻辑结构：线性结构，定长的线性表

二维数组既可以看作非线性结构也可以看作线性结构：
1）线性结构:二维数组中的每一个元素都可以看作是定长的线性表
2）非线性结构：二维数组中的每一个元素既在一个行表中也在一个列表中（不止有一个前驱和一个后继：从行看，有一个前驱后继，从列看，也有一个前驱后继，这就不是一对一的关系了）：

我们可以把数组看成是一种特殊的线性结构，是线性结构的扩展。
二维数组的几种定义方式：（有一种是套娃，先定义列再定义行）

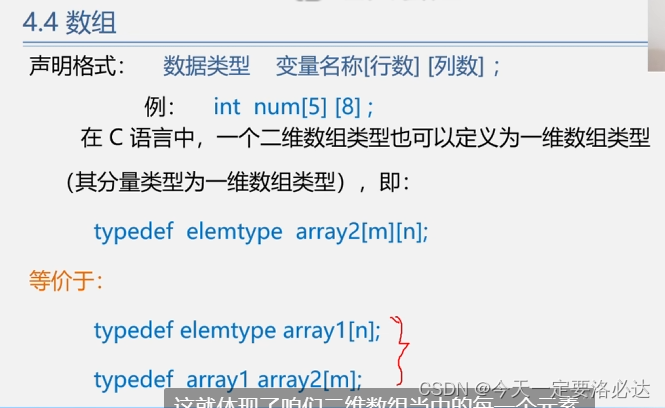
关于三维和更高维度：
三维数组：二维数组中的元素又是一个一维数组，那么这就叫做三维数组。
n维数组：n-1维数组中的元素又是一个一维数组，那么这就叫做n维数组。

数组和线性表的关系：
线性表结构是数组结构的一个特例，数组结构是线性表结构的扩展。

数组特点：
结构是固定的，定义之后，维数和维界（每一维的长度是多少）不会再改变

数组操作：
数组结构是固定的，所以一般没有插入和删除的操作。一般只有初始化，销毁，修改元素等操作。

2.2、数组的抽象数据类型定义

代码如下（示例）：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
import  ssl
ssl._create_default_https_context = ssl._create_unverified_context

2.3、数组的顺序存储

数组很少使用链式存储结构，也不插入和删除运算（因为结构固定）
数组一般使用顺序存储结构
数组是多维的，但是存储元素的内存单元地址是一维的，在存储之前，需要将多维映射到一维

一维数组的存储运算：

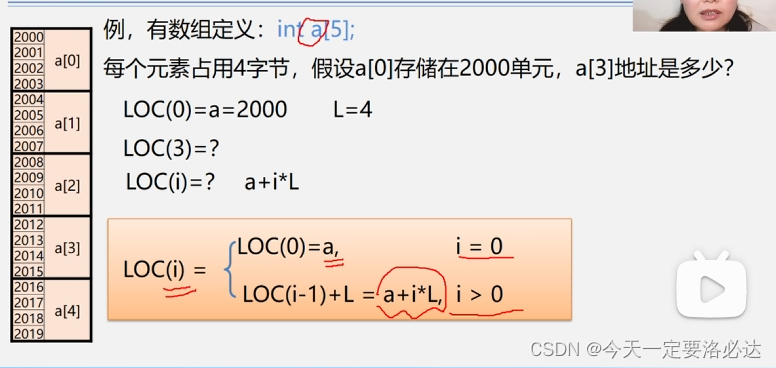
（这里a+i*L为什么不是(i-1)呢，因为i是从0开始的）

二维数组的存储运算：
一共两种存储方式：
1）行优先（java,c等）：先把行存满
2）列优先：先把列存满

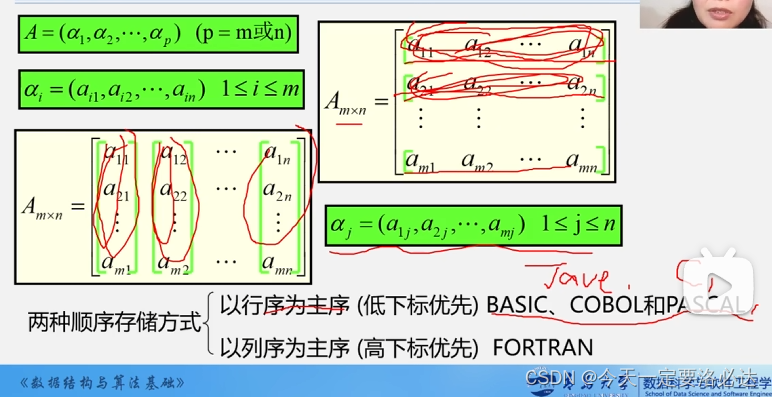
行优先：

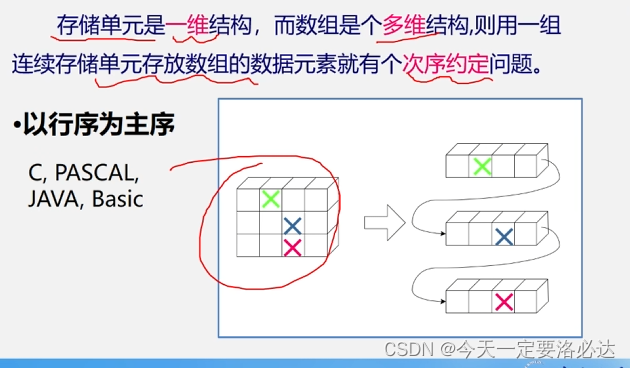
列优先：

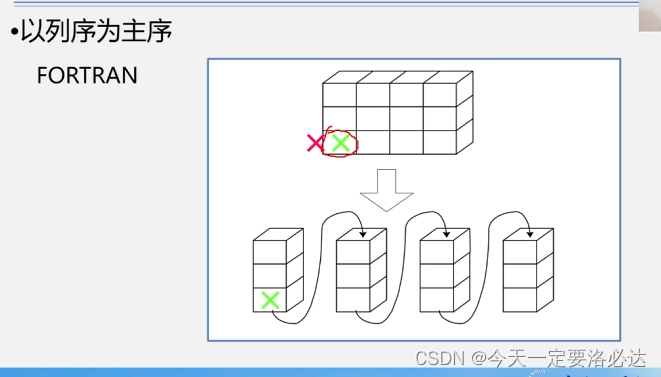
所以最终二维数组的存储计算方式：

三维数组的存储运算：

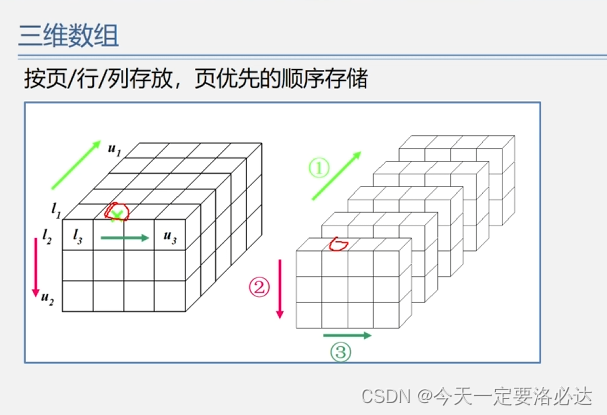
n维数组的存储运算：

例题：

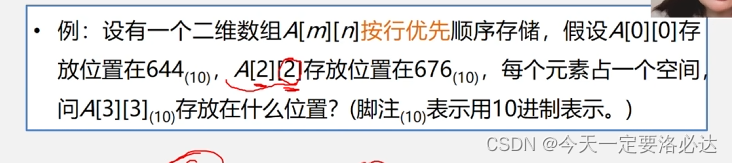
2n+2+644=676
n=15
A[3][3]放在 644+3*15+3=692

2.4、特殊矩阵的压缩存储

矩阵：一个m*n元素排成的m行n列的表
矩阵的常规存储： 用二维数组

用数组来存储矩阵（常规存储） 的好处：
1）可以随机存取
2）矩阵运算很方便：一般就是存取
3）存储密度为1（不需要存储其他东西，比如地址等）

不适合常规存储的矩阵：
1）零元素多
2）值相同的元素很多且呈某种规律
这样常规存储太浪费空间，这里我们就可以考虑矩阵的压缩存储了。
可以压缩存储的矩阵：对称矩阵，对角矩阵，三角矩阵，稀疏矩阵

1）对称矩阵：（只存上三角或者下三角）

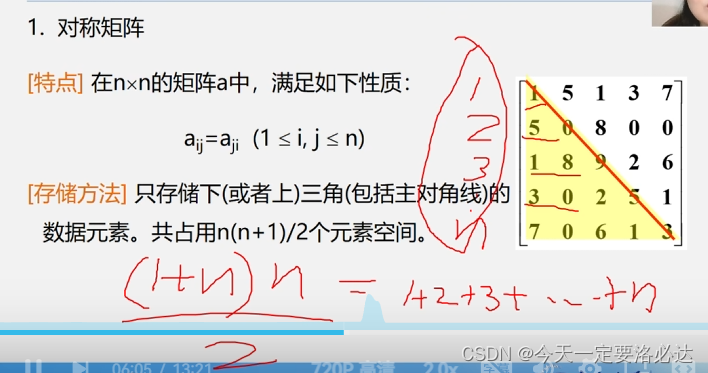
我们一般是拿一位数组去存储这个对称矩阵的，那一般是怎么算的呢：
这里以下图的an1为例子：

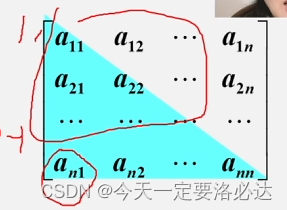
(1+(n-1)) (n-1)/2 = n*(n-1)/2 就是用高斯公式求就行了
2）三角矩阵：
三角矩阵定义：对角线以下或者以上部分的数据元素全部为常数C（这时我们不用把所有元素都存起来）

这里的存储方式和前面堆对称矩阵很像，也是把所有元素放到一个一位数组中。

存储方式：

3）对角矩阵：


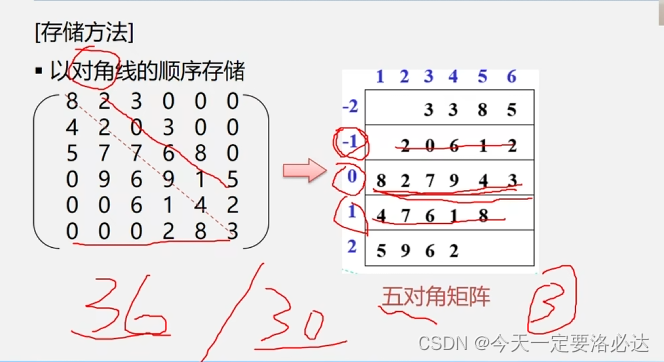
存储方法：先把对角线的元素先存起来，然后再存其它的，这里从36个元素压缩到了30个元素，这里是五对角矩阵，压缩的情况还不是很明显，如果换成三对角还是什么就明显了

4）稀疏矩阵：
稀疏矩阵就是0特别多的矩阵

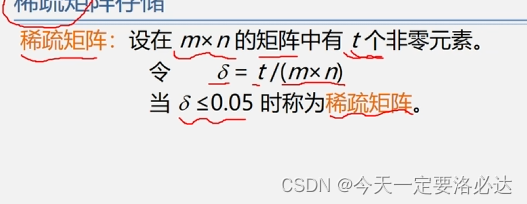
超过95%的元素都是0。

稀疏矩阵可以通过三元组的方式来存储：（三元组就是i,j,aij）

这里例子中的矩阵存储密度是40%左右，其实看起来存储的还挺多的，但是我们还是能看出来有很大的浪费了

三元组法：一般还需要在第0行存储总行数，总列数，非零元素个数（三元组法一般又称为有序的双下标法）

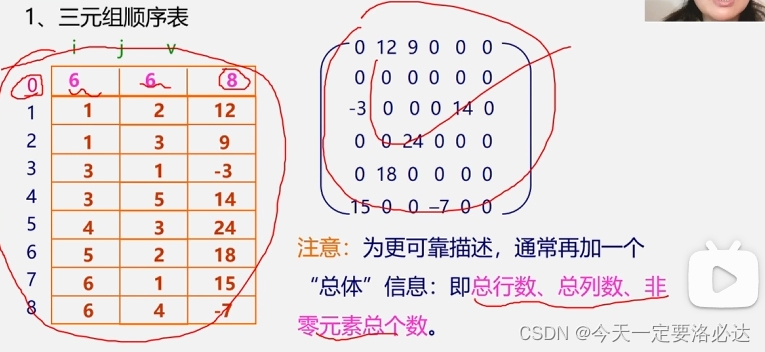
同理我们可以根据三元组还原出稀疏矩阵：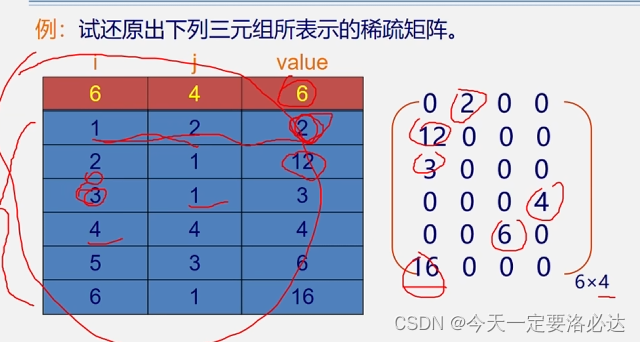
三元组的优缺点：
1）优点：非零元素是按行存储，便于依行进行处理的矩阵运算
2）缺点：不能随机存取，必须从头开始
这里的缺点其实是可以克服的，所以有了十字链表

5）十字链表
三元组表的插入和删除是比较麻烦的
但是十字链表的插入和删除就比较简单

十字链表有五个部分：

十字链表的例子：（因为有十字交叉，所以被成为十字链表）

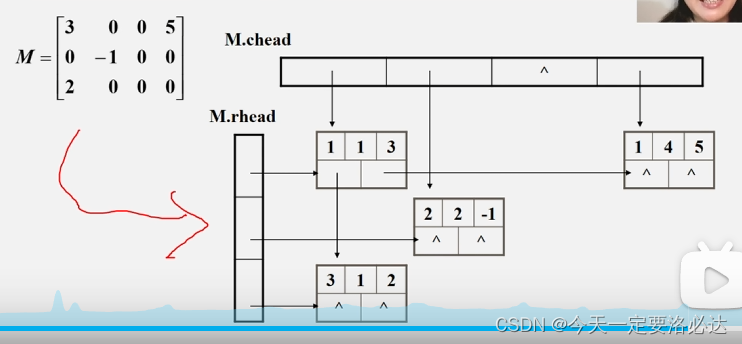
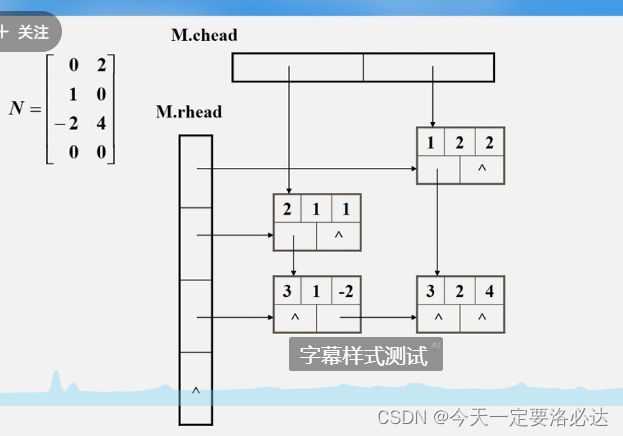
三、广义表

广义表是一个递归定义：用自己定义自己

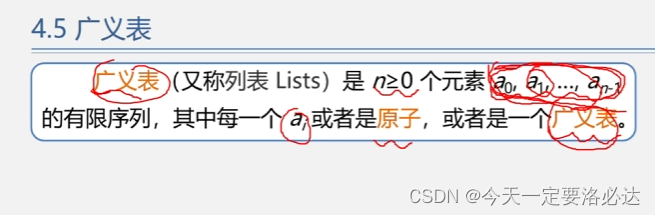
广义表也是线性表的推广，和线性表不同的是，线性表中的元素类型都是一致的，广义表不一定。

举例子：

注意广义表的表尾和线性表的表尾有点不太一样

一般用大写字母表示广义表，小写字母表示原子，下面是一个例子：

（5）是共享广义表
（6）是递归广义表

广义表的性质：
1）广义表的元素有顺序，一个直接前驱和一个直接后继
2）广义表的长度
3）广义表的深度
原子的深度为0，空表的深度为1
4）广义表的共享
5）广义表的递归
6）广义表的多层次结构

（5）这里长度为2，深度无穷

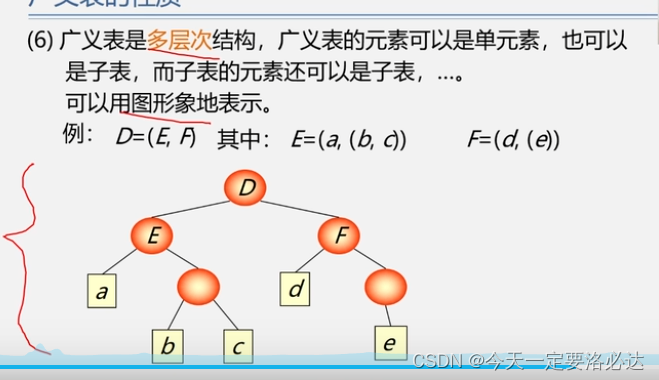
广义表和线性表的区别：
广义表是线性表的推广，线性表是广义表的特例

广义表的基本运算：

广义表的存储：
没法用数组存储（广义表的元素不是一样大小）
一般用链式存储

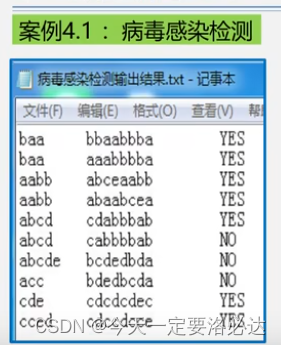
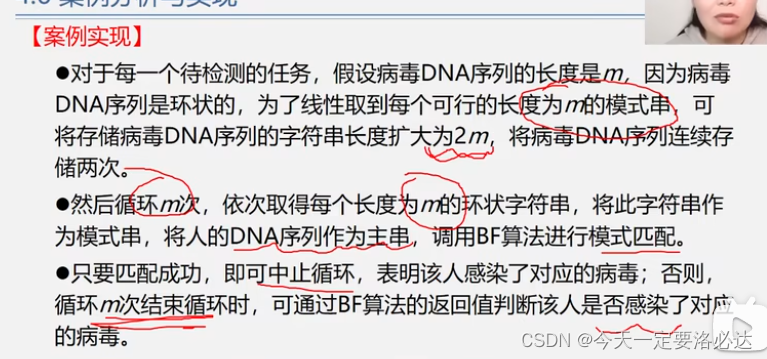
四、病毒案例

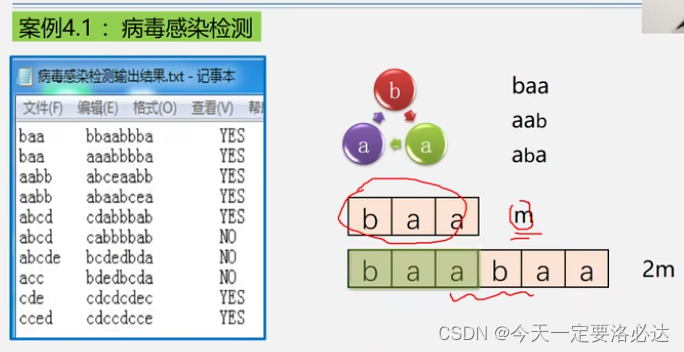
这个案例的特殊点在于病毒是环状的，我们的模式串就有很多种可能
案例实现：（我们生成多一倍存储空间的2m，进行扫描检测，每次扫m个数据，这样就行了）