前言
最近注意到了NumSharp,想学习一下,最好的学习方式就是去实践,因此从github上找了一个用python实现的简单线性回归代码,然后基于NumSharp用C#进行了改写。
NumSharp简介
NumSharp(NumPy for C#)是一个在C#中实现的多维数组操作库,它的设计受到了Python中的NumPy库的启发。NumSharp提供了类似于NumPy的数组对象,以及对这些数组进行操作的丰富功能。它是一个开源项目,旨在为C#开发者提供在科学计算、数据分析和机器学习等领域进行高效数组处理的工具。

python代码
用到的python代码来源:llSourcell/linear_regression_live: This is the code for the “How to Do Linear Regression the Right Way” live session by Siraj Raval on Youtube (github.com)
下载到本地之后,如下图所示:
python代码如下所示:
#The optimal values of m and b can be actually calculated with way less effort than doing a linear regression.
#this is just to demonstrate gradient descentfrom numpy import *# y = mx + b
# m is slope, b is y-intercept
def compute_error_for_line_given_points(b, m, points):totalError = 0for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]totalError += (y - (m * x + b)) ** 2return totalError / float(len(points))def step_gradient(b_current, m_current, points, learningRate):b_gradient = 0m_gradient = 0N = float(len(points))for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]b_gradient += -(2/N) * (y - ((m_current * x) + b_current))m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))new_b = b_current - (learningRate * b_gradient)new_m = m_current - (learningRate * m_gradient)return [new_b, new_m]def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):b = starting_bm = starting_mfor i in range(num_iterations):b, m = step_gradient(b, m, array(points), learning_rate)return [b, m]def run():points = genfromtxt("data.csv", delimiter=",")learning_rate = 0.0001initial_b = 0 # initial y-intercept guessinitial_m = 0 # initial slope guessnum_iterations = 1000print ("Starting gradient descent at b = {0}, m = {1}, error = {2}".format(initial_b, initial_m, compute_error_for_line_given_points(initial_b, initial_m, points)))print ("Running...")[b, m] = gradient_descent_runner(points, initial_b, initial_m, learning_rate, num_iterations)print ("After {0} iterations b = {1}, m = {2}, error = {3}".format(num_iterations, b, m, compute_error_for_line_given_points(b, m, points)))if __name__ == '__main__':run()
用C#进行改写
首先创建一个C#控制台应用,添加NumSharp包:
现在我们开始一步步用C#进行改写。
python代码:
points = genfromtxt("data.csv", delimiter=",")
在NumSharp中没有genfromtxt方法需要自己写一个。
C#代码:
//创建double类型的列表List<double> Array = new List<double>();// 指定CSV文件的路径string filePath = "你的data.csv路径";// 调用ReadCsv方法读取CSV文件数据Array = ReadCsv(filePath);var array = np.array(Array).reshape(100,2);static List<double> ReadCsv(string filePath)
{List<double> array = new List<double>();try{// 使用File.ReadAllLines读取CSV文件的所有行string[] lines = File.ReadAllLines(filePath); // 遍历每一行数据foreach (string line in lines){// 使用逗号分隔符拆分每一行的数据string[] values = line.Split(',');// 打印每一行的数据foreach (string value in values){array.Add(Convert.ToDouble(value));} }}catch (Exception ex){Console.WriteLine("发生错误: " + ex.Message);}return array;
}
python代码:
def compute_error_for_line_given_points(b, m, points):totalError = 0for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]totalError += (y - (m * x + b)) ** 2return totalError / float(len(points))
这是在计算均方误差:
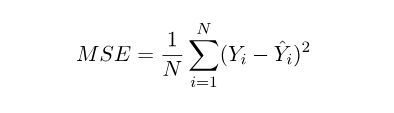
C#代码:
public static double compute_error_for_line_given_points(double b,double m,NDArray array){double totalError = 0;for(int i = 0;i < array.shape[0];i++){double x = array[i, 0];double y = array[i, 1];totalError += Math.Pow((y - (m*x+b)),2);}return totalError / array.shape[0];}
python代码:
def gradient_descent_runner(points, starting_b, starting_m, learning_rate, num_iterations):b = starting_bm = starting_mfor i in range(num_iterations):b, m = step_gradient(b, m, array(points), learning_rate)return [b, m]
def step_gradient(b_current, m_current, points, learningRate):b_gradient = 0m_gradient = 0N = float(len(points))for i in range(0, len(points)):x = points[i, 0]y = points[i, 1]b_gradient += -(2/N) * (y - ((m_current * x) + b_current))m_gradient += -(2/N) * x * (y - ((m_current * x) + b_current))new_b = b_current - (learningRate * b_gradient)new_m = m_current - (learningRate * m_gradient)return [new_b, new_m]
这是在用梯度下降来迭代更新y = mx + b中参数b、m的值。
因为在本例中,误差的大小是通过均方差来体现的,所以均方差就是成本函数(cost function)或者叫损失函数(loss function),我们想要找到一组b、m的值,让误差最小。
成本函数如下:
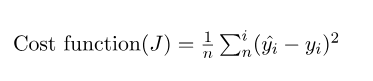
对θ1求偏导,θ1就相当于y = mx + b中的b:
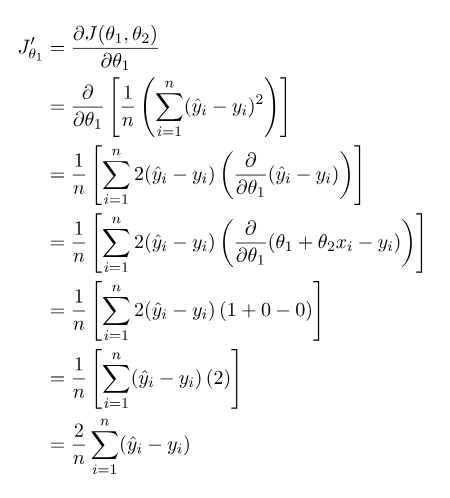
再对θ2求偏导,θ2就相当于y = mx + b中的m:
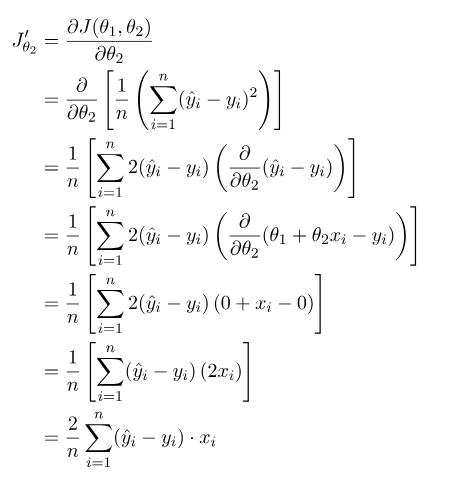
使用梯度下降:
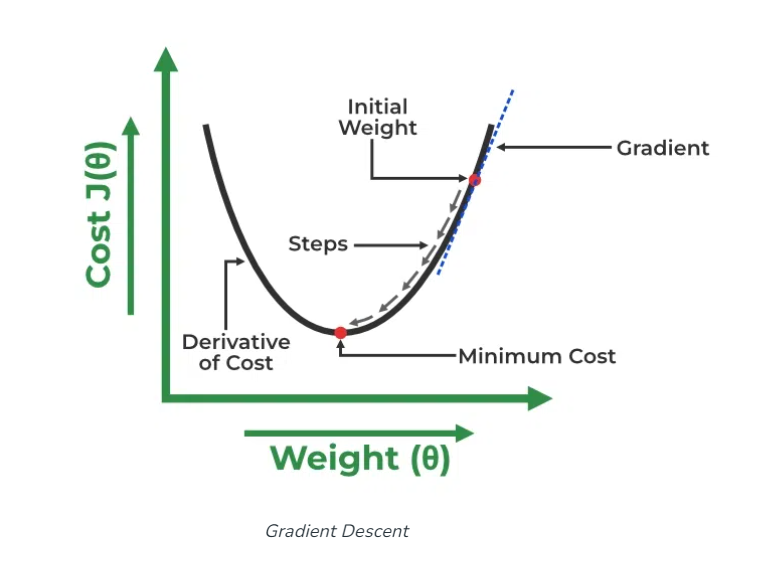
θ1与θ2的表示:
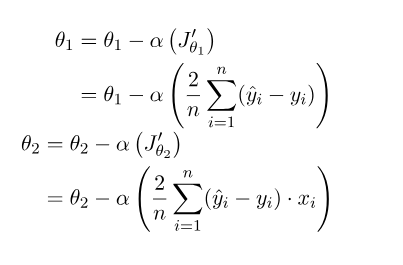
α是学习率,首先θ1、θ2先随机设一个值,刚开始梯度变化很大,后面慢慢趋于0,当梯度等于0时,θ1与θ2的值就不会改变了,或者达到我们设置的迭代次数了,就不再继续迭代了。关于原理这方面的解释,可以查看这个链接(Linear Regression in Machine learning - GeeksforGeeks),本文中使用的图片也来自这里。
总之上面的python代码在用梯度下降迭代来找最合适的参数,现在用C#进行改写:
public static double[] gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate,double num_iterations){double[] args = new double[2];args[0] = starting_b;args[1] = starting_m;for(int i = 0 ; i < num_iterations; i++) {args = step_gradient(args[0], args[1], array, learningRate);}return args;}
public static double[] step_gradient(double b_current,double m_current,NDArray array,double learningRate){double[] args = new double[2];double b_gradient = 0;double m_gradient = 0;double N = array.shape[0];for (int i = 0; i < array.shape[0]; i++){double x = array[i, 0];double y = array[i, 1];b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));}double new_b = b_current - (learningRate * b_gradient);double new_m = m_current - (learningRate * m_gradient);args[0] = new_b;args[1] = new_m;return args;}
用C#改写的全部代码:
using NumSharp;namespace LinearRegressionDemo
{internal class Program{ static void Main(string[] args){ //创建double类型的列表List<double> Array = new List<double>();// 指定CSV文件的路径string filePath = "你的data.csv路径";// 调用ReadCsv方法读取CSV文件数据Array = ReadCsv(filePath);var array = np.array(Array).reshape(100,2);double learning_rate = 0.0001;double initial_b = 0;double initial_m = 0;double num_iterations = 1000;Console.WriteLine($"Starting gradient descent at b = {initial_b}, m = {initial_m}, error = {compute_error_for_line_given_points(initial_b, initial_m, array)}");Console.WriteLine("Running...");double[] Args =gradient_descent_runner(array, initial_b, initial_m, learning_rate, num_iterations);Console.WriteLine($"After {num_iterations} iterations b = {Args[0]}, m = {Args[1]}, error = {compute_error_for_line_given_points(Args[0], Args[1], array)}");Console.ReadLine();}static List<double> ReadCsv(string filePath){List<double> array = new List<double>();try{// 使用File.ReadAllLines读取CSV文件的所有行string[] lines = File.ReadAllLines(filePath); // 遍历每一行数据foreach (string line in lines){// 使用逗号分隔符拆分每一行的数据string[] values = line.Split(',');// 打印每一行的数据foreach (string value in values){array.Add(Convert.ToDouble(value));} }}catch (Exception ex){Console.WriteLine("发生错误: " + ex.Message);}return array;}public static double compute_error_for_line_given_points(double b,double m,NDArray array){double totalError = 0;for(int i = 0;i < array.shape[0];i++){double x = array[i, 0];double y = array[i, 1];totalError += Math.Pow((y - (m*x+b)),2);}return totalError / array.shape[0];}public static double[] step_gradient(double b_current,double m_current,NDArray array,double learningRate){double[] args = new double[2];double b_gradient = 0;double m_gradient = 0;double N = array.shape[0];for (int i = 0; i < array.shape[0]; i++){double x = array[i, 0];double y = array[i, 1];b_gradient += -(2 / N) * (y - ((m_current * x) + b_current));m_gradient += -(2 / N) * x * (y - ((m_current * x) + b_current));}double new_b = b_current - (learningRate * b_gradient);double new_m = m_current - (learningRate * m_gradient);args[0] = new_b;args[1] = new_m;return args;}public static double[] gradient_descent_runner(NDArray array, double starting_b, double starting_m, double learningRate,double num_iterations){double[] args = new double[2];args[0] = starting_b;args[1] = starting_m;for(int i = 0 ; i < num_iterations; i++) {args = step_gradient(args[0], args[1], array, learningRate);}return args;}}
}
python代码的运行结果:

C#代码的运行结果:

结果相同,说明改写成功。
总结
本文基于NumSharp用C#改写了一个用python实现的简单线性回归,通过这次实践,可以加深对线性回归原理的理解,也可以练习使用NumSharp。


![[UI5] ODATA V4中的CRUD](http://pic.xiahunao.cn/[UI5] ODATA V4中的CRUD)



:简洁优雅,功能强大的编程语言)







)



)
