单调栈练习（五）— 子数组的最小值之和

题目
同样的LeetCode原题：题目链接

给定一个整数数组 arr，找到 min(b) 的总和，其中 b 的范围为 arr 的每个（连续）子数组。

由于答案可能很大，因此返回答案模 10^9 + 7 。

在这里插入图片描述

思路

暴力解
先来说暴力解的思路：
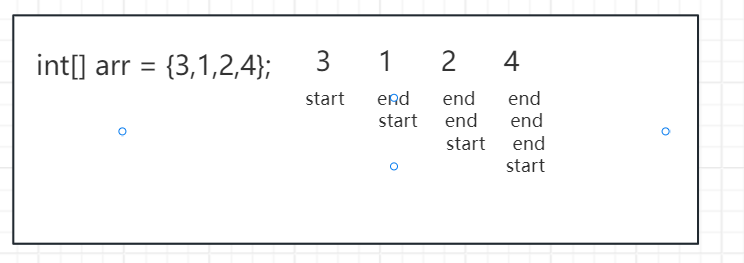
三层for循环，找到每一个子数组中的最小值，0-0，0-1，0-2 … 0-N。1-1，1-2，1-3…1-N。并将每一个子数组的最小值相加即可，时间复杂度 $O(N^3)$ 。

在这里插入图片描述

代码

public static int subArrayMinSum2(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int ans = 0;for (int i = 0; i < N; i++) {for (int j = i; j < N; j++) {int min = arr[i];for (int k = i + 1; k <= j; k++) {min = Math.min(min, arr[k]);}ans += min;}}return ans;}

优化的普通解

优化的方法是根据题目中给定的 arr[]，生成对应的 left[] 和 right[]。

left[]：left[i] = x ，表示左侧最近 <= arr[i] 的位置在 x（x表示对应的索引）
right[]：right[i] = y，表示右侧最近 < arr[i] 的位置在y（y表示对应的索引）

生成 left[] 和 right[]的作用在于，根据当前子数组中最小值 arr[i] 在 left[]、right[]中获取左右最小且近的边界值后，直接进行计算求出以 arr[i] 作为子数组最小值的累加和，优化后的时间复杂度是 $O (N)$ 。

来看下面的例子：当前 arr[8] = 7 ，找到左侧最近且小的值在是4位置的3，右侧最近且小的值是12位置4。
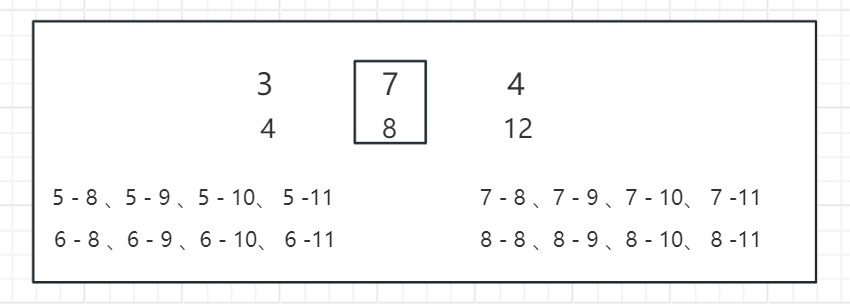
在这里插入图片描述

此时，以7作为最小值的子数组范围是 5 ~ 11，并且此范围内所有值都是 >= 7 的，但是因为要以7作为最小值，所以5 ~ 11范围内所求的子数组要把8位置的7涵盖进去。此时利用 left[8] = 4 、right[8] = 12，（8 - 4）x（12 - 8）x (arr[8]) = 112，就是7作为最小值的时候所有子数组最小值的累加和。

需要注意的是：如果是普通的无重复值数组，那么很好处理，但如果数组中有重复值，就需要额外注意！！！

举例：
在这里插入图片描述
碰上有重复值的数组，要稍微多考虑一些，就是左右边界的设定选择改怎么选？本题中答案选用的是第一种

两种选择的不同其实目的都是一个，那就是抛去重复值的计算

比如说：
此时以4位置的3作为最小值，如果依然是从1位置开始枚举每个子数组 1 - 4 、 1 - 5 … 1 - 11，那等到以7位置的3作为最小值时呢？此时如果再从1 - 7、 1 - 8 … 1 - 11。那么和之前计算的子数组最小值就包含了重复的部分。所以要去重。

代码

构建完成后，遍历一遍 arr[] ，将每一个值都作为子数组的最小值，并根据 left[]、right[] 算出子数组的个数，个数 * 最小值，不就是我们想要的答案，再将求出来的每一个结果进行累加。

 public static int subArrayMinSum2(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int[] left = leftNearLessEqual1(arr);int[] right = rightNearLess1(arr);int ans = 0;for (int i = 0; i < arr.length; i++) {int start = i - left[i];int end = right[i] - i;ans += start * end  * arr[i];}return ans;}public static int[] rightNearLess1(int[] arr) {int N = arr.length;int[] right = new int[N];int ans;for (int i = 0; i < N; i++) {ans = N;for (int j = i + 1; j < N; j++) {if (arr[j] < arr[i]) {ans = j;break;}}right[i] = ans;}return right;}public static int[] leftNearLessEqual1(int[] arr) {int N = arr.length;int[] left = new int[N];int ans;for (int i = N - 1; i >= 0; i--) {ans = -1;for (int j = i - 1; j >= 0; j--) {if (arr[j] <= arr[i]) {ans = j;break;}}left[i] = ans;}return left;}

单调栈
单调栈其实就是将构建left[]、right[]的过程加快了，其逻辑是不变的。
这里的单调栈是自己用数组实现，没有用系统提供的Stack，但是照比系统提供的性能要更好一些。

 public static int sumSubarrayMins(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int[] stack = new int[arr.length];int[] left = leftNearLessEqual2(arr, stack);int[] right = rightNearLess2(arr, stack);long ans = 0;for (int i = 0; i < arr.length; i++) {long start = i - left[i];long end = right[i] - i;ans += (start * end) * arr[i];ans %= 1000000007;}return (int)ans;}public static int[] rightNearLess2(int[] arr,int[] stack) {int N = arr.length;int[] right = new int[N];int size = 0;for (int i = 0; i < N; i++) {while (size != 0 && arr[i] < arr[stack[size - 1]]){right[stack[--size]] = i;}stack[size++] = i;}while (size != 0){right[stack[--size]] = N;}return right;}public static int[] leftNearLessEqual2(int[] arr,int[] stack) {int N = arr.length;int[] left = new int[N];int size = 0;for (int i = N - 1; i >= 0; i--) {//stack[size - 1] ：当前最后加入到数组中元素即为栈顶元素//stack[--size] ：出栈操作，弹出栈顶元素并且大小 - 1，后加入的元素要覆盖当前位置while (size != 0 && arr[i] <= arr[stack[size - 1]]){//当前 i 位置 使栈顶元素出栈，所以 left[栈顶元素左侧小且近] = 当前下标 ileft[stack[--size]] = i;}//入栈操作：存储当前元素索引stack[size++] = i;}while (size != 0){left[stack[--size]] = -1;}return left;}