目录
一，栈（Stack）
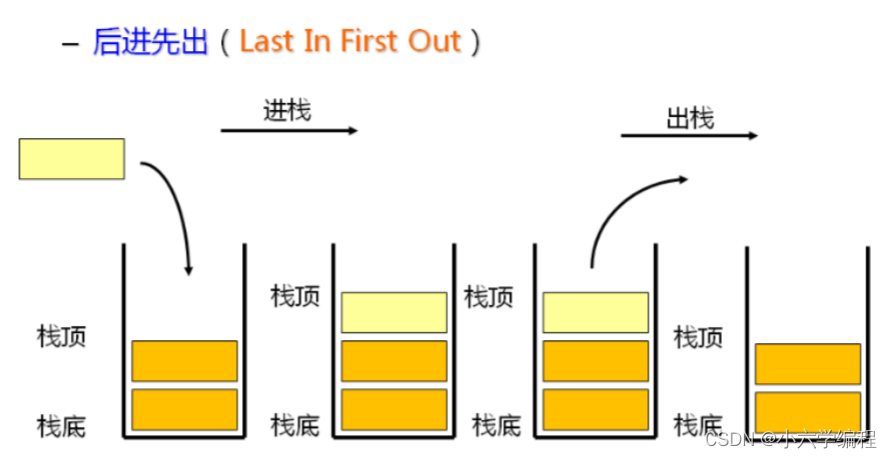
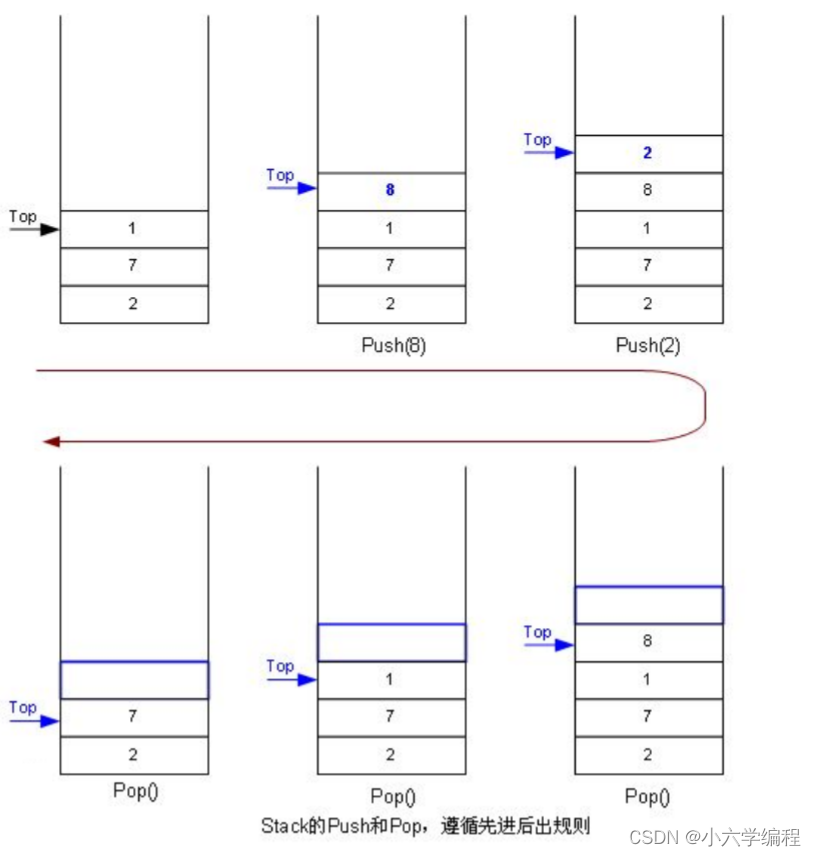
1.1 概念
1.2 栈的使用
1.3 栈的模拟实现
1.4 栈的应用场景
1.5 栈，虚拟机栈，栈帧有什么区别？
二，队列（Queue）
2.1 概念
2.2 队列的使用
2.3 队列模拟实现
2.4 循环队列
三，双端队列
一，栈（Stack）
1.1 概念
栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈
顶，另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据在栈顶。
1.2 栈的使用
| 方法 | 功能 |
| Stack() | 构造一个空的栈 |
| E push(E e) | 将 e 入栈，并返回 e |
| E pop() | 将栈顶元素出栈并返回 |
| E peek() | 获取栈顶元素 |
| int size() | 获取栈中有效元素个数 |
| boolean empty() | 检测栈是否为空 |
public static void main(String[] args) {
Stack<Integer> s = new Stack();
s.push(1);
s.push(2);
s.push(3);
s.push(4);
System.out.println(s.size()); // 获取栈中有效元素个数---> 4
System.out.println(s.peek()); // 获取栈顶元素---> 4
s.pop(); // 4出栈，栈中剩余1 2 3，栈顶元素为3
System.out.println(s.pop()); // 3出栈，栈中剩余1 2 栈顶元素为3
if(s.empty()){
System.out.println("栈空");
}else{
System.out.println(s.size());
}
}
1.3 栈的模拟实现
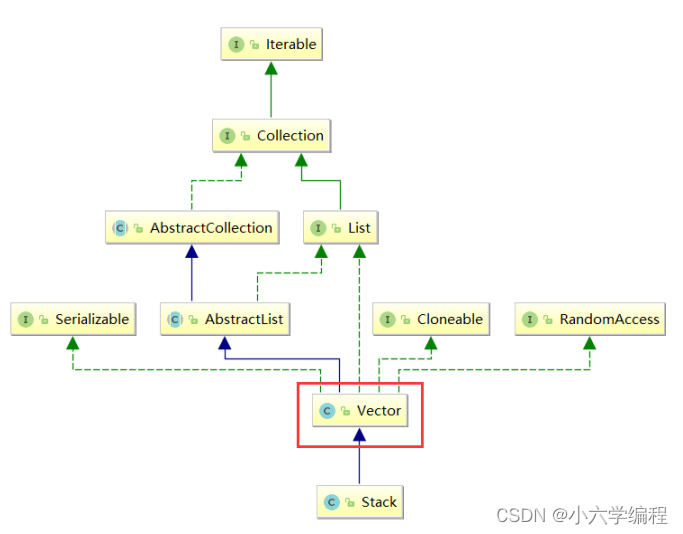
从上图中可以看到，Stack继承了Vector，Vector和ArrayList类似，都是动态的顺序表，不同的是Vector是线程安全的。
接口实现：
public interface IStack {//入栈public int push(int val);//出栈public int pop();//获取栈顶元素public int peek();//获取栈内有多少元素public int size();//检查栈是否为空public boolean empty();//已满扩容public void full();
}import java.util.Arrays;public class MyStack implements IStack{int[] array;int size;static final int capacity = 3;public MyStack() {array = new int[capacity];}//入栈@Overridepublic int push(int val) {if (isFull()) {full();}array[size] = val;size++;return val;}//出栈//先进先出@Overridepublic int pop() throws EmptyStackException{if (empty()) {throw new EmptyStackException("空栈异常");} else {int val = array[size-1];array[size-1] = 0;size--;return val;}}//获取栈顶元素@Overridepublic int peek() throws EmptyStackException{if (empty()) {throw new EmptyStackException("空栈异常");} else {return array[size - 1];}}//获取栈内有多少元素@Overridepublic int size() {return size;}//检查栈是否为空@Overridepublic boolean empty() {return size == 0;}@Overridepublic void full() {if (isFull()) {//扩容array = Arrays.copyOf(array,array.length * 2);}}//检查栈是否已满private boolean isFull() {return size() == capacity;}//打印栈public void display() {for (int i = 0; i < size; i++) {System.out.print(array[i] + " ");}System.out.println(" ");}
}1.4 栈的应用场景
1. 括号匹配
思路：
我们先来看看括号不匹配的案例
我们只需要解决以上三种问题就能完成该题
于是我们想到了使用栈来解决
遍历字符串，将左括号放进栈中
又遇到左括号，继续放进栈中
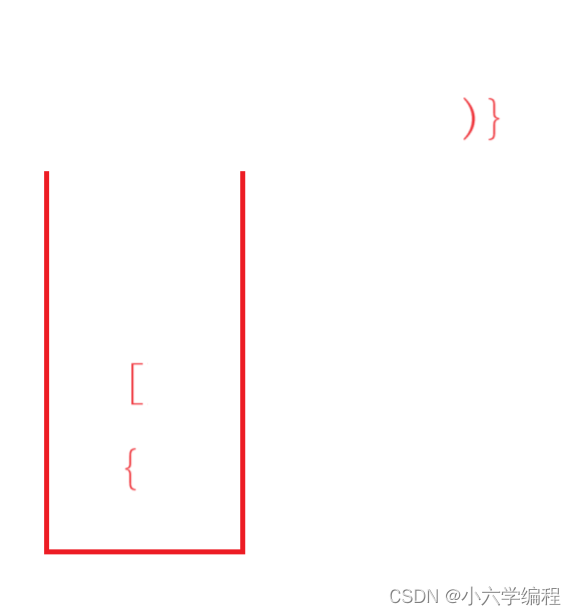
此时遇到右括号
将栈顶括号与此时遍历遇到的括号进行比较
发现括号并不匹配，故返回false
而另外一种情况：
当字符串遍历完后栈为空，则返回true
public boolean isValid(String s) {Stack<Character> sta = new Stack<>();//遍历字符串for (int i = 0; i < s.length(); i++) {//判断是不是左括号char ch = s.charAt(i);if (ch == '{' || ch == '[' || ch == '(') {sta.push(ch);} else {//遇到右括号if (sta.empty()) {return false;} else {char ch2 = sta.peek();if ((ch2 == '(' && ch == ')') || (ch2 == '[' && ch == ']') || (ch2 == '{' && ch == '}')) {sta.pop();} else {return false;}}}}if (!sta.empty()) {return false;}return true;}
}2.逆波兰表达式求值
首先我们要明白一点，什么是逆波兰表达式
逆波兰表示法（Reverse Polish notation，RPN，或逆波兰记法），是一种是由波兰数学家扬·武卡谢维奇1920年引入的数学表达式形式，在逆波兰记法中，所有操作符置于操作数的后面，因此也被称为后缀表示法。逆波兰记法不需要括号来标识操作符的优先级。
这是一个我们常见的表达式：9+(3-1)*3+8/2，这是一个中缀表达式，而我们要将它转换成一个不需要括号来识别优先级的后缀表达式，该怎么做？
记住一点：先加上括号再都去除括号
当我们拿到后缀表达式后就能真正利用栈来进行求值
首先计算机会遍历字符串
当遇到的是一个数字，就会把它放进栈里
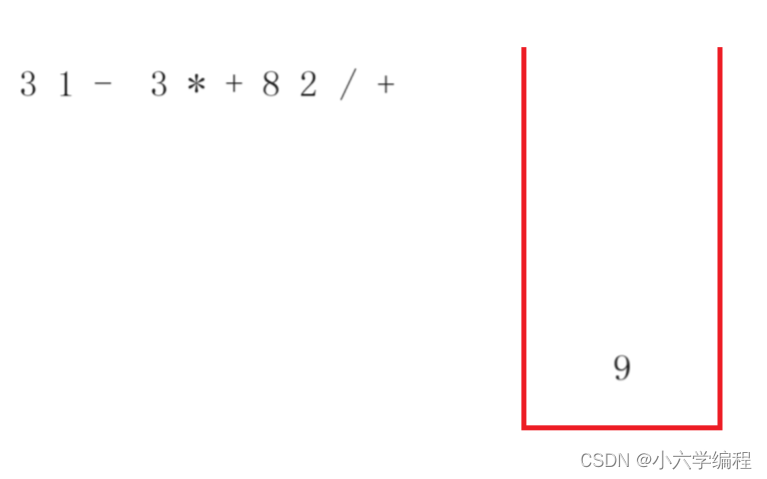
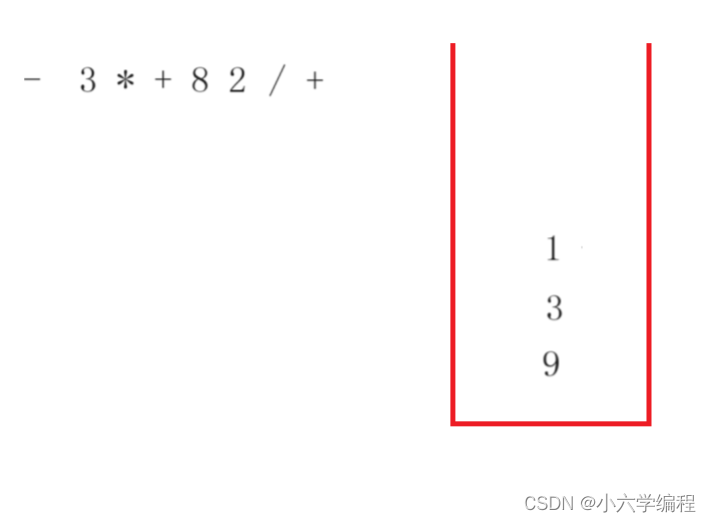
当遇到运算符，就会让栈顶两个元素对该运算符进行运算
然后将运算得到的这个数字再次放进栈中
继续遍历
……
直到字符串遍历完后栈中只剩下一个元素，该元素就是该表达式的运算结果
根据以上，我们就能完成该题：
import java.util.Stack;class Solution {public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>();for (String x:tokens) {if (!isOperator(x)) {stack.push(Integer.parseInt(x));} else {int num2 = stack.pop();int num1 = stack.pop();switch (x) {case "+" :stack.push(num1 + num2);break;case "-" :stack.push(num1 - num2);break;case "*" :stack.push(num1 * num2);break;case "/" :stack.push(num1 / num2);break;}}}return stack.pop();}private boolean isOperator(String s) {if (s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")) {return true;}return false;}
}3.出栈入栈次序匹配
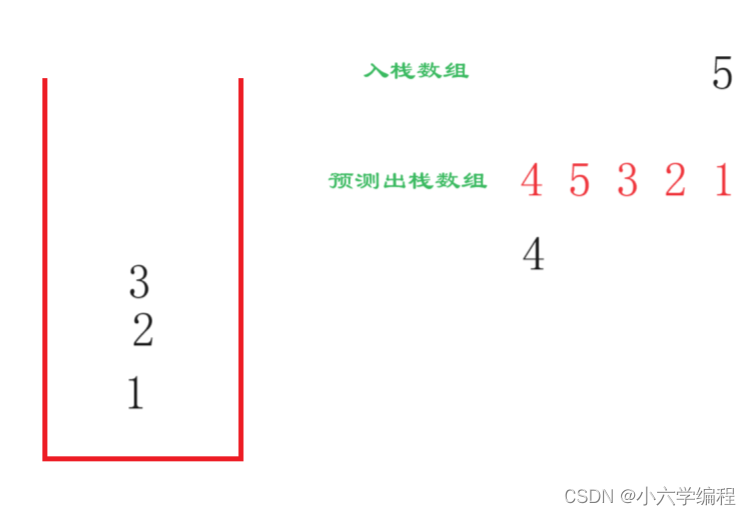
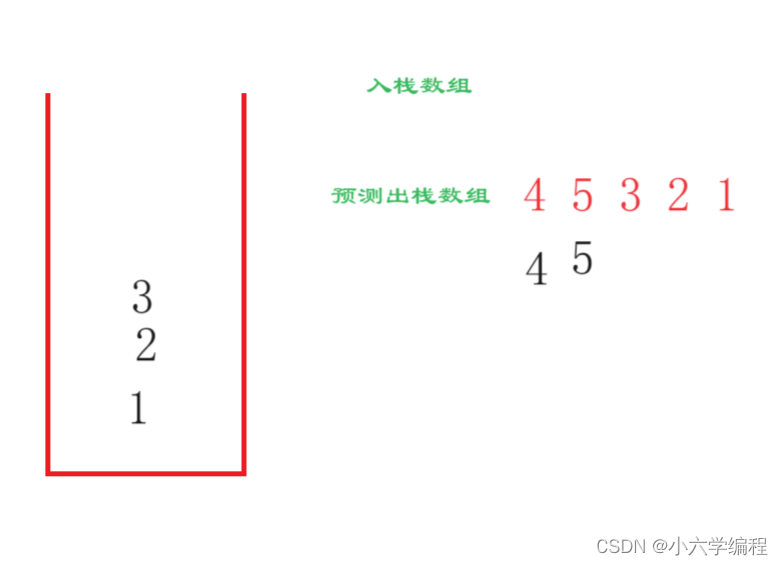
由上图，预测第一个出栈的数组元素是4
遍历入栈数组，4及4之前的元素的都入栈
栈顶元素4和出栈数组元素第一个相同，出栈
栈顶元素与出栈数组第二个元素不相同，入栈数组再次入栈
栈顶元素与出栈数组第二个元素相同，故出栈，此时入栈数组已遍历完成，故只需判断入栈数组次序与栈顶到栈底元素次序是否相同即可
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可*** @param pushV int整型一维数组* @param popV int整型一维数组* @return bool布尔型*/public boolean IsPopOrder (int[] pushV, int[] popV) {// write code hereStack<Integer> stack = new Stack<>();int i = 0;for (int x:pushV) {stack.push(x);int tmp = stack.size();for (int j = 0; j < tmp; j++) {if (stack.peek() == popV[i]) {stack.pop();i++;} else {break;}}}for (int j = 0; j < stack.size(); j++) {if (stack.pop() != popV[i]) {return false;} else {i++;}}return true;}
}4.最小栈
该题实现Stack各功能比较简单，关键还是如何实现这个最小栈上
建立如下图两个栈
普通栈用来实现栈的各功能，最小栈用来存放每次入栈的最小值
具体怎么实现？
当我们放入第一个元素时，在两个栈当中都放入，此时minStack中栈顶元素就是stack中的最小值
随后放入第二个元素时间就与minStack中栈顶元素进行比较，如果较小，就在两个栈当都放入
随后第三个元素比minStack栈顶元素大，就只放入普通栈
按此思路
……
此时放入的元素和minStack栈顶元素相等，故两个栈都放入
代码实现：
import java.util.Stack;class MinStack {private Stack<Integer> stack;private Stack<Integer> minStack;public MinStack() {stack = new Stack<>();minStack = new Stack<>();}public void push(int val) {stack.push(val);if (minStack.empty()) {minStack.push(val);} else {if (val <= minStack.peek()) {minStack.push(val);}}}public void pop() {int val = minStack.peek();if (stack.peek() == val) {stack.pop();minStack.pop();} else {stack.pop();}}public int top() {return stack.peek();}public int getMin() {if (!minStack.empty()) {return minStack.peek();} else {return -1;}}
}
1.5 栈，虚拟机栈，栈帧有什么区别？
| 栈 | 数据结构 |
| 虚拟机栈 | JVM划分的一块内存 |
| 栈帧 | 调试方法时会在虚拟机当中给这个方法开辟一块内存 |
二，队列（Queue）
2.1 概念
队列：只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out) 入队列：进行插入操作的一端称为队尾（Tail/Rear） 出队列：进行删除操作的一端称为队头（Head/Front）
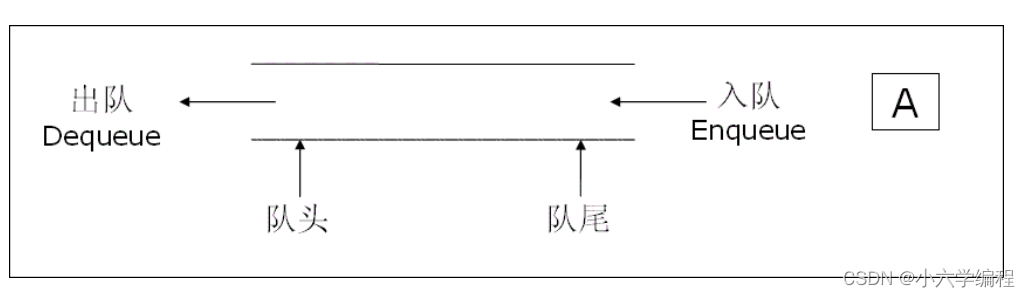
2.2 队列的使用
在Java中，Queue是个接口，底层是通过链表实现的。
| 方法 | 功能 |
| boolean offer(E e) | 入队列 |
| E poll() | 出队列 |
| peek() | 获取队头元素 |
| int size() | 获取队列中有效元素个数 |
| boolean isEmpty() | 检测队列是否为空 |
注意：Queue是个接口，在实例化时必须实例化LinkedList的对象，因为LinkedList实现了Queue接口。
public static void main ( String [] args ) {Queue < Integer > q = new LinkedList <> ();q . offffer ( 1 );q . offffer ( 2 );q . offffer ( 3 );q . offffer ( 4 );q . offffer ( 5 ); // 从队尾入队列System . out . println ( q . size ());System . out . println ( q . peek ()); // 获取队头元素q . poll ();System . out . println ( q . poll ()); // 从队头出队列，并将删除的元素返回if ( q . isEmpty ()){System . out . println ( " 队列空 " );} else {System . out . println ( q . size ());}}
2.3 队列模拟实现
队列中既然可以存储元素，那底层肯定要有能够保存元素的空间，通过前面线性表的学习了解到常见的空间类型有两种：顺序结构 和 链式结构。
思考：队列的实现使用顺序结构还是链式结构好？
class Queue {//双向链表节点public static class ListNode {ListNode prev;ListNode next;int val;ListNode(int val) {this.val = val;}}ListNode first; // 队头ListNode last; // 队尾int size = 0;// 入队列---向双向链表位置插入新节点public void offer(int e){ListNode node = new ListNode(e);if (first == null) {first = node;} else {last.next = node;}last = node;size++;}// 出队列---将双向链表第一个节点删除掉public int poll() {// 1. 队列为空if (first == null) {return -1;}int val = first.val;// 2. 队列中只有一个元素----链表中只有一个节点---直接删除if (first == last) {first = null;last = null;} else {// 3. 队列中有多个元素---链表中有多个节点----将第一个节点删除first = first.next;first.prev.next = null;first.prev = null;}size--;return val;}// 获取队头元素---获取链表中第一个节点的值域public int peek() {if (first == null) {return -1;}return first.val;}public int getSize() {return size;}public boolean isEmpty(){ return first == null; }
}2.4 循环队列
上列代码是由双向链表来进行实现的，那我们可不可以用线性表（数组）来实现呢？
实际中我们有时还会使用一种队列叫循环队列。如操作系统课程讲解生产者消费者模型时可以就会使用循环队列。环形队列通常使用数组实现。
数组下标循环的小技巧
1. 下标最后再往后 (offset 小于 array.length): index = (index + offset) % array.length
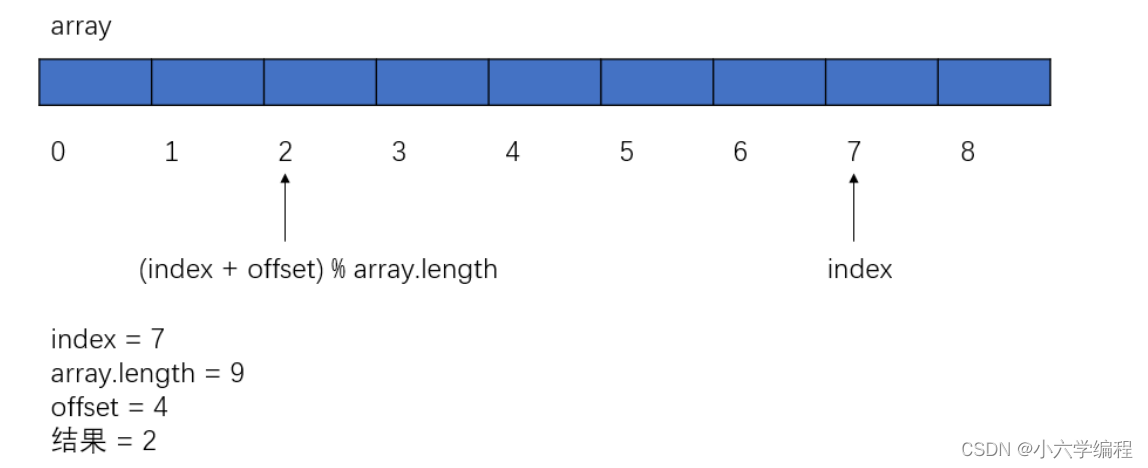
2. 下标最前再往前(offset 小于 array.length): index = (index + array.length - offset) % array.length
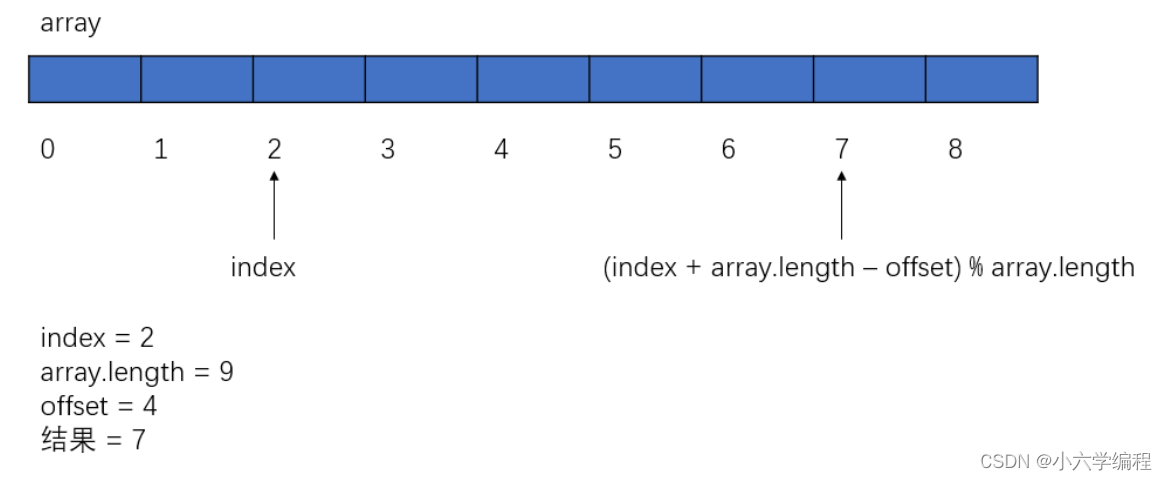
如何区分空与满
1. 通过添加 size 属性记录
2. 保留一个位置
3. 使用标记
关于方法2：
设计循环队列
代码示例：
class MyCircularQueue {public int[] elem;public int front;//队头public int rare;//队尾public MyCircularQueue(int k) {elem = new int[k + 1];}public boolean enQueue(int value) {if (isFull()) {return false;}elem[rare] = value;rare = (rare + 1) % elem.length;return true;}public boolean deQueue() {if (isEmpty()) {return false;}elem[front] = 0;front = (front + 1) % elem.length;return true;}public int Front() {if (isEmpty()) {return -1;}return elem[front];}public int Rear() {if (isEmpty()) {return -1;}int index = (rare == 0) ? elem.length - 1 : rare - 1;return elem[index];}public boolean isEmpty() {return front == rare;}public boolean isFull() {return (rare + 1) % elem.length == front;}
}
三，双端队列
双端队列（ deque ）是指允许两端都可以进行入队和出队操作的队列， deque 是 “double ended queue” 的简称。那就说明元素可以从队头出队和入队，也可以从队尾出队和入队。
Deque是一个接口，使用时必须创建LinkedList的对象。
在实际工程中，使用Deque接口是比较多的，栈和队列均可以使用该接口
Deque<Integer> stack = new ArrayDeque<>();// 双端队列的线性实现Deque<Integer> queue = new LinkedList<>();// 双端队列的链式实现
完。
