论文题目:A Real-Time Motion Planner with Trajectory Optimization for Autonomous Vehicles
Abstract
本文的实时规划器首先将空间离散化,然后基于一组成本函数搜索出最佳轨迹。迭代优化所得到的轨迹的Path和Speed。post-optimization计算复杂度低,能够在几次迭代内收敛到一个更高质量的解,该框架可以减少52%的规划时间,提高规划质量。
本文主要的创新点就在于post-optimization
I INTRODUCTION
A Background
规划器需要满足严格的实时要求,以便在紧急情况做出足够快的反应。
B Related work
Autonomous driving Systems:对自动驾驶系统的发展做了一些调研。单纯的自适应巡航控制系统和车道辅助系统无法执行复杂的驾驶行为(处理并车、绕开其他汽车、能够智能的对意外的动态障碍物作出反应),这些系统仍需要人类监督执行。
Trajectory generation:道路场景中自动驾驶的轨迹生成需要考虑三个约束:运动学、动力学和道路形状。具体来说,就是曲率和加速度的变化率在轨迹中应该是连续的
[3][4]提出了利用曲率多项式保证曲率变化率连续的逆路径生成方法。
(1)基于[3][4]的方法,[5][6]提出的规划器首先沿道路采样端点,然后使用曲率多项式连接它们,便于所有的路径符合道路形状;然后给每条路径指定不同的加速度曲线来生成一组轨迹。
(2)[6]中生成的路径可以被车辆很好地跟踪。但是由于加速度曲线不连续,车辆很难准确、平稳地跟随加速度曲线。
(3)[7]使用另一种方法处理这个问题,使用五次多项式生成横向d(t)和纵向轨迹s(t),确保了连续地加速度曲线。此外他们使用道路中心线为参考的Frenet坐标系结合横向和纵向运动。使得轨迹纵向与道路形状一致。然而,每个轨迹上的每个点的曲率需要被计算和验证,计算量大。另外,虽然曲率是连续的,但是曲率的一阶导(和方向盘转角相关)频繁改变,导致方向盘移动不平稳。
Search algorithm:轨迹生成之后,通常应用搜索算法来找到最优结果。state lattice planners通常基于启发式(A和ARA[8])或采样(RRT[9])。
(1)基于启发式的搜索算法,对成本的准确估计从任何一个顶点到目标都是必不可少的。但自动驾驶规划问题很复杂,特别是当存在动态障碍物时,很难找到适合所有场景的适当启发式函数。
(2)一些增量重规划算法(D*Lite[10])广泛应用于机器人导航,但它们仅适用于具有一个固定目标的典型规划问题,但是在道路场景下,目标会一直变化。
(3)基于采样的方法(RRT[9]),规划结果通常不够平滑,无法让汽车执行。另外,==由于动态障碍物的存在,需要在搜索状态空间中加入时间作为额外的维度。==使得搜索空间呈指数增长,导致基于搜索的算法效率低下。因此,本文应用状态空间的离散化,然后应用简单而快速的穷举搜索。
Optimization method for planning:[11]提出了一种共轭梯度法来平滑路径。然而,车辆的速度没有规划或优化。因此,该算法在道路环境中不能很好地工作,速度对于驾驶非常重要,特别是处理动态障碍物。[12]提出了用于运动规划的梯度优化方法,能够更好地避免静态障碍物。但是,他们的方法也没有考虑时间维度或者速度。
C Contribution
在related work的基础上,提出了一种实时的运动规划器。该Planner具有以下特点:(1)由规划器生成的轨迹是平滑且连续的,在运动学上可以被车辆执行(2)通过有效路径和速度离散化加速最优轨迹搜索(3)通过post-optimization补偿离散化牺牲的性能(4)通过在路径和速度空间中迭代优化来提高实时性能。
II Algorithm Framework

实时运动规划器如上图所示,由轨迹规划和轨迹优化两部分组成,第一步,使用[3]中描述的方法生成路径边缘;然后为每个路径边生成速度集;将一组成本函数应用在每个轨迹上,并选择最佳轨迹。然后将生成的最佳轨迹传递到优化模块,在优化模块中,使用随机-定向单纯形优化算法迭代优化路径和速度[13]。
A Trajectory generation
Path Set和Speed Set分别生成,然后通过将Path Set和Speed Set相结合获得轨迹集。
(1)路径生成:通过使用不同种类的曲率多项式连接采样端点来生成路径。规划器中的抽样方法与[5]中的相同。然而,代替三次,四次曲率多项式用于确保每个规划周期的起始点处的曲率变化率是连续的。
(a)端点采样:执行了采样机制为了生成每条路径的顶点(端点),道路中心线的函数如下:

使用类似Frenet的方式去定义一个空间的点:

对于每一层,对垂直于中心线的 N p a t h N_{path} Npath进行采样
(b)路径模型:通过连接以下各项来生成路径
1)成对的采样端点
2)端点和当前车辆姿态
该运动规划器采用三次和四次曲率多项式构建路径模型。对于三次曲率多项式,路径的曲率是弧长的三次多项式
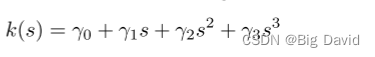
因此,问题变成找到满足端点约束的参数。函数中有4个参数: r 0 , r 1 , r 2 , r 3 r_0,r_1,r_2,r_3 r0,r1,r2,r3,s不算,论文这边感觉有错误,其中有五个约束项对应x,y的移动,起点到终点的方向,起点的曲率和终点的曲率。
在以前的工作[5]中,只有三次曲率多项式用于常见场景。该方法适用于任何单一规划周期,==然而在两个规划周期的接合点处可能发生不连续性。==运动规划器以非常高的频率重新规划,结果,实际规划结果远远达不到平滑的效果。下图显示了使用四次曲率多项式(红色实线)的典型结果,比使用三次多项式(蓝色虚线)平滑地多。

因此,需要对当前车辆姿态和端点之间的路径添加新的约束,即,当前车辆姿态点处曲率的一阶导数。为了满足这个额外的约束,多项式需要是四次而不是三次。当我们频繁地重新规划这种改进可以让路径变得平滑。如下图所示,红色路径表示四次曲率多项式,而绿色路径是三次曲率多项式,然而,四次多项式需要更多的时间来生成,因此,为了限制计算时间,四次多项式仅用于从当前车辆姿态开始的轨迹段

(2)速度生成:在生成路径集之后,为每个单独的路径构建候选速度曲线,与[5][14]做的工作不同,他们使用正向方法生成速度曲线。本文使用逆向方法。首先将速度空间离散化,然后生成多项式满足顶点约束。本文的方法也不同于[15]和[7]中提出的逆方法,后者使用时间的多项式函数来生成速度曲线。本文使用弧长的多项式函数与本文的路径方程更加一致。多项式方程如下:

速度状态: Q = ( s , v , a ) Q=(s,v,a) Q=(s,v,a),对于每条路径,从路径的起点选择起始速度状态 Q i n i t = ( s 0 , v 0 , a 0 ) Q_{init}=(s_0,v_0,a_0) Qinit=(s0,v0,a0),从路径的终点选择终止速度状态 Q g o a l = ( s 1 , v 1 , a 1 ) Q_{goal}=(s_1,v_1,a_1) Qgoal=(s1,v1,a1)。在上式,有四个未知参数,对应的四个约束是: v 0 , a 0 , v 1 , a 1 v_0,a_0,v_1,a_1 v0,a0,v1,a1。对于所有顶点,v0和v1来自相应的离散化顶点,a0和a1设置为0。车辆当前状态 ( v 0 , a 0 ) (v_0,a_0) (v0,a0)的特殊之处:他们是从真实的车辆传感器上获得的。将最大速度和最小速度分别表示为 v m a x v_{max} vmax和 v m i n v_{min} vmin,并且将离散化速度的数量表示为 N s p e e d N_{speed} Nspeed,离散化速度如下:

通过设置 s 0 = 0 s_0=0 s0=0,可以获得参数:

速度和候选速度曲线的离散化如下图所示,其中绿色点是采样速度,红色曲线超出加速度限制,灰色曲线是有效曲线。这种速度生成方法确保了持续的加速。

B Cost function set
对于每条轨迹,定义了静态成本和动态成本,用来评估安全性、舒适性、效率、能耗和行为。从每一条轨迹中提取n个点来表示成本。如下表所示静态和动态成本的计算公式。

静态成本:
(1)路径长度->效率
(2)曲率->舒适性
(3)曲率一阶导->舒适性
(4)与最近中心线的横向偏移->行为
(5)到静态障碍物的转换距离
动态成本:
(1)时间->效率
(2)速度->能量
(3)加速度->舒适性
(4)jerk->舒适性
(5)到动态障碍物的转换距离->安全性
静态成本 c o b s s c^s_{obs} cobss和动态成本 c o b s d c^d_{obs} cobsd用于对每个候选轨迹的碰撞检查。基于[16]提出的方法,使用 M c i r M_{cir} Mcir圆来覆盖车辆的区域。如果圆到障碍物的距离小于阈值 d m i n A l l o w e d d_{minAllowed} dminAllowed,则成本是无限的。否则用下式计算成本。

其中 λ o b s s λ^s_{obs} λobss和 λ o b s d λ^d_{obs} λobsd分别是静态和动态障碍物的指数成本函数的带宽, g j g_j gj是障碍物与覆盖汽车的第 j j j个圆之间的距离
一个轨迹的总成本是所有项的加权和:

C Trajectory optimization
对于大多数Lattice planner,适当的离散化是必要的,用来确保实时性。然而适当的离散化影响了规划结果的最优性。post-optimize轨迹提高性能非常重要。
一个直接的方法就是同时优化轨迹路径和速度。然后,对于实时性来说是十分耗时的。计算开销为 O ( o p t ( M + N ) ) O(opt(M+N)) O(opt(M+N)),其中M为路径参数个数,N为速度参数个数, o p t ( ) opt() opt()为优化算法的计算复杂度,通常为 O ( N 2 ) O(N^2) O(N2)。随着维数的增加,优化器也更难找到全局最优解。
因此,本文提出了一种迭代轨迹优化机制。计算复杂度是 O ( o p t ( M ) ) + O ( o p t ( N ) ) O(opt(M)) +O(opt(N)) O(opt(M))+O(opt(N))。如果在规划阶段找到的轨迹接近真实的最优,则使用该机制允许在几次迭代中收敛到真实的最优
(1)路径优化:路径离散化限制了路径的最优性,例如,采样端点的横向偏移、航向和曲率是固定的,并且与中心线有一定的关系。因此,放松这些约束,如下图,并在新端点之间生成新路径可以提高轨迹质量。:

因为成本与横向偏移和航向的梯度很难计算,因此使用非导数优化算法(单纯形算法[17])进行路径优化。如下图所示,路径优化后的路径(红线)更加平滑

(2)速度优化:速度离散化和端点处的加速度约束也限制了速度曲线的最优性。与路径优化类似,优化速度剖面节点的参数。对于生成当前最低成本的速度曲线的节点,优化速度和加速度的值。因此连接新节点能让速度曲线保持平滑。
在此优化中,节点处的速度变化将影响轨迹上每个点的时间,这改变了轨迹上动态障碍物的位置,并阻止了梯度方法的使用。因此,非导数单纯形算法也用于速度优化。速度优化结果如下图所示,由于放松了对端点加速度的约束,速度变化更加平滑,端点处的速度幅值不再离散

D Optimization performance evaluation
实验表明提出的规划与迭代优化框架是非常有前途的。与替代规划机制或配置相比,它能够在更短的时间内生成更高质量的轨迹。与非优化结果相比,时间减少52%并且质量提高10%。
III System Implementation
A Interfacing with Autonomous Vehicle
配备了高保真定位系统。它还使用激光雷达和雷达来感知实时周围环境。飞行器的下层控制被设计成执行高精度轨迹跟踪。因此,运动规划器仅需要生成具有路径和速度轮廓的可执行轨迹。
规划器和下游的控制器之间的接口被构建为使得在每个规划周期期间,发送轨迹的第一部分,其取决于车辆速度为8-50米。这给予下游的控制器足够的前瞻性来执行预测控制算法。增加了系统的可靠性,因为较低级别的控制器总是有一个相对较长的轨迹来执行,即使较高级别的计算机停止工作几个周期。
B Robust replan mechanism
为了对真实的世界中动态变化的环境做出反应,运动规划器需要不断地重新规划。如果规划器从当前车辆状态开始规划,那么当规划完成时,通常在100毫秒左右,车辆将处于不同的位置,原来的规划不再有效。为了解决这个问题,[18]提出了PMP(部分运动规划)方案。简而言之,他们的做法是从未来状态开始规划。当规划器运行时,车辆执行上一个规划周期的轨迹。
规划起点问题
基于[18],实现了弧长升序的队列,以保留上一个计划周期的轨迹。对于每个周期,首先在队列中找到最接近车辆位置的具有弧长 s c s_c sc的点 P c l o s e P_{close} Pclose。然后,规划器在队列中寻找具有弧长 s f s_f sf的点 P f u t u r e P_{future} Pfuture,该点与 P c l o s e P_{close} Pclose相比处于较晚的位置。计算 s f s_f sf的公式为:
 其中 V c u r r V_{curr} Vcurr是车辆的当前速度, a m a x a_{max} amax是车辆可以达到的最大加速度,而 t s p a n t_{span} tspan是当前时间和下一次重新计划的开始时间之间的基本时间跨度,其应该长于重新计划间隔。该等式确保在需要其结果之前完成规划。最后,规划器从 P f u t u r e P_{future} Pfuture重传,并使用最新规划的轨迹更新轨迹队列。
其中 V c u r r V_{curr} Vcurr是车辆的当前速度, a m a x a_{max} amax是车辆可以达到的最大加速度,而 t s p a n t_{span} tspan是当前时间和下一次重新计划的开始时间之间的基本时间跨度,其应该长于重新计划间隔。该等式确保在需要其结果之前完成规划。最后,规划器从 P f u t u r e P_{future} Pfuture重传,并使用最新规划的轨迹更新轨迹队列。
有一种特殊情况,当车辆处于手动驾驶模式时,不是从未来位置规划,而是从其当前状态(位置和速度)重新规划。这确保了车辆在从手动模式切换到自动模式时始终具有可行的轨迹来执行,即使车辆正在移动。
IV EXPERIMENTAL RESULTS
本文测试了三个不同的场景:车道驾驶,静态障碍物和动态障碍物。
A:Lane driving
车道驾驶测试在S形弯曲道路上进行。人类驾驶员通常能够选择更短更平滑的路线。结果如下图所示:

自动驾驶汽车在道路的内部移动,以获得更短的路径长度,并且在进入时减速,在退出曲线时加速。自动驾驶汽车能够跟踪规划器生成的轨迹,平均交叉轨迹误差小于10厘米,最大跟踪误差约为40厘米,平均速度误差约为0.5米/秒。规划器生成的轨迹对小车执行是可行的。
B:Static obstacles
在道路环境中,自动驾驶员需要处理多个静态障碍物,包括路缘、停放的汽车和道路堵塞。在这个规划器中,道路上的不可驾驶区域,例如破碎的路面,也被建模为静态障碍物。测试的规划器的性能处理弯曲的道路和多个静态障碍物在一起。结果如下图所示,红点为静态障碍物。

为了避开静态障碍物,自动驾驶汽车没有在弯道上走捷径,而是选择了一条更长但仍然平滑的路径。
C:Dynamic obstacles
对于自动驾驶车辆,动态障碍物通常是移动障碍物,例如汽车、行人、骑自行车的人或骑摩托车的人。如下图所示,在该测试中,车辆在其首选(上)车道上遇到较慢的汽车。

由于前面速度较慢的车辆限制了自动驾驶汽车的前进,规划者选择一条变道轨迹来绕过它。自动驾驶汽车在通过开始时加速,然后在通过速度较慢的车辆时保持近似匀速,并在通过后加速。由于横向距离成本的存在,在超车慢车时,它也倾向于保持在绕行车道的中心,这是合理的。
V Conclusion
本文提出并实现了一种实用的具有轨迹优化的实时自主驾驶运动规划器。由规划器生成的轨迹是平滑和连续的,使得自主车辆能够以非常小的路径和速度跟踪误差执行。对速度和路径空间进行了适当的离散化,使得搜索最优轨迹的速度更快。为了进一步提高轨迹的质量,设计并实现了速度和路径状态空间的迭代优化。实验结果表明,采用迭代优化框架后,生成轨迹的性能提高了10%,规划时间减少了50%以上。该规划器已在模拟和真实的车辆在三种情况下进行了测试。它能够处理带有急转弯的弯曲道路,避免多个道路上的静态障碍物,并执行变道和规避较慢的汽车。
未来的工作,需要做更多的道路上的实验,以验证规划器的性能,在处理复杂的真实的交通场景。规划器的性能也可以通过在速度和路径空间中应用更有效的修剪来提高。虽然成本函数确定最终轨迹的选择,但是手动找到成本函数的适当形式和权重是困难和主观的。因此,未来的研究也将集中在从人类驾驶员演示中学习成本函数。
算法详解)













)

(GetMem与FreeMem))


