【数据结构】二叉树问题总结

目录

1.二叉树前序遍历，中序遍历和后序的实现

2.层序遍历

3.求二叉树中的节点个数

4.求二叉树中的叶子节点个数

5.求二叉树的高度

6.求二叉树第k层节点个数

7.二叉树查找值为x的节点

8.单值二叉树

9.二叉树最大深度

10.翻转二叉树

11. 检查两颗树是否相同

12. 对称二叉树

13. 另一颗树的子树

14.二叉树的前序遍历

15.通过前序遍历的数组构建二叉树 

16.判断二叉树是否是完全二叉树

17.判断二叉树是否是平衡二叉树 

18.二叉树销毁  

1.二叉树前序遍历，中序遍历和后序的实现

我们回顾以下二叉树的遍历：

前序遍历（先序遍历）：访问根节点的操作发生在遍历其左右子树之前

中序遍历：访问根节点的操作发生在遍历其左右子树之间

后序遍历：访问根节点的操作发生在遍历其左右子树之后

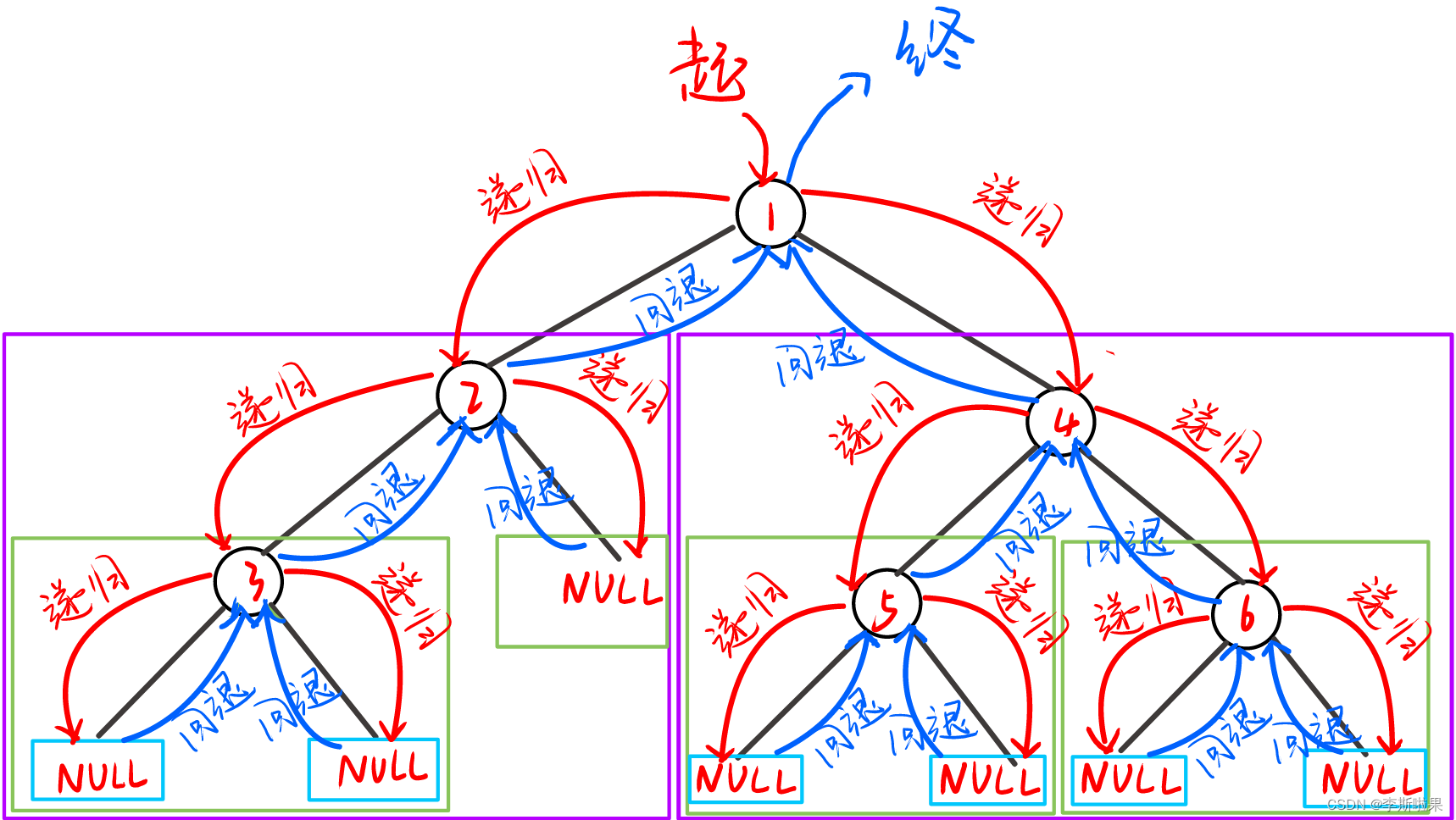
二叉树的遍历通过递归实现，下图为二叉树前序的递归遍历图解：

从根节点开始，先遍历根节点，再遍历左子树，左子树的遍历又分为先遍历根节点再遍历左子树，以根左子树右子树的顺序递归遍历，直至根节点为NULL

前序递归遍历的参考代码如下：

#include<stdio.h>
#include<stdlib.h>//快速构建一棵二叉树
typedef int DataType;
typedef struct TreeNode
{struct TreeNode* left;struct TreeNode* right;DataType data;
}TreeNode;//创建节点
TreeNode* BuyNode(DataType x)
{TreeNode* newnode = (TreeNode*)malloc(sizeof(TreeNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}//快速构建一棵树
TreeNode* CreateBinaryTree()
{TreeNode* n1 = BuyNode(1);TreeNode* n2 = BuyNode(2);TreeNode* n3 = BuyNode(3);TreeNode* n4 = BuyNode(4);TreeNode* n5 = BuyNode(5);TreeNode* n6 = BuyNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n2->right = NULL;n3->left = NULL;n3->right = NULL;n4->left = n5;n4->right = n6;n5->left = NULL;n5->right = NULL;n6->left = NULL;n6->right = NULL;return n1;
}//二叉树的前序遍历
TreeNode* PreOrder(TreeNode* root)
{if (root == NULL){printf("NULL ");return;}printf("%d ", root->data);PreOrder(root->left);PreOrder(root->right);}int main()
{TreeNode* root = CreateBinaryTree();PreOrder(root);return 0;
}

 输出结果如下：

同理，可以使用递归实现 中序遍历和后序遍历

//二叉树的中序遍历
TreeNode* InOrder(TreeNode* root)
{if (root == NULL){printf("NULL ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);}
//二叉树的后序遍历
TreeNode* PostOrder(TreeNode* root)
{if (root == NULL){printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);}

2.层序遍历

二叉树的层序遍历要基于队列实现，上一层节点出队，其孩子节点依次入队，依次访问直到队列为空

📖Note：

采用链式队列实现时，队列中每个元素的数据域存放的是二叉树节点的指针，类型为TreeNode* 

// 队列的定义
typedef struct QueueNode
{TreeNode* data;struct QueueNode* next;
}QNode;typedef struct Queue
{QNode* head;QNode* tail;
}Queue;
// 层序遍历
void BinaryTreeLevelOrder(TreeNode* root)
{Queue q;QueueInit(&q);//根节点入队if (root){QueuePush(&q, root);}//队列不为空时while (!QueueEmpty(&q)){//访问队头元素并出队TreeNode* front = QueueFront(&q);QueuePop(&q);printf("%d", front->val);//队头元素的孩子节点入队if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestroy(&q);
}

 队列相关操作如下：

//队列初始化
void QueueInit(Queue* pq)
{assert(pq);pq->head = pq->tail = NULL;
}
//判断队列是否为空
bool QueueEmpty(Queue* pq)
{assert(pq);return pq->head == NULL && pq->tail == NULL;
}
//队列销毁
void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->head;while (cur){QNode* del = cur;cur = cur->next;free(del);}pq->head = pq->tail = NULL;
}
//访问队头数据
TreeNode* QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->head->data;}
//数据入队
void QueuePush(Queue* pq, TreeNode* x)
{assert(pq);QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");exit(-1);}else{newnode->data = x;newnode->next = NULL;}//空队列时插入if (pq->tail == NULL){pq->head = pq->tail = newnode;}//非空队列时插入else{pq->tail->next = newnode;//链接新元素pq->tail = newnode;//更新队尾}
}
//数据出队
void QueuePop(Queue* pq)
{assert(pq);//空队列不能进行出队操作assert(!QueueEmpty(pq));//队列中只有一个元素if (pq->head->next == NULL){free(pq->head);pq->head = pq->tail = NULL;}else{QNode* del = pq->head;pq->head = pq->head->next;free(del);del = NULL;}
}

 

3.求二叉树中的节点个数

求一棵树中的节点个数，有两种解决思路

  1. 暴力求解，遍历计数
  2. 转换成子问题求解

暴力求解时，变量size的定义可能出现问题，定义1如下：

函数中直接定义size，每次递归调用函数size都被置0，所以最后的返回结果为1，不能求出二叉树的长度

//求二叉树节点个数
int TreeSize(TreeNode* root)
{int size = 0;if (root == NULL){return 0;}size++;TreeSize(root->left);TreeSize(root->right);return size;}

定义2：将size定义成静态变量，但仍在函数内

这种定义方法解决了每次函数内递归size置0的问题，但是static定义的变量只有在第一次定义的时候才会初始化，所以当我们在其他函数中重复调用TreeSize函数时，size的值会累加

解决方法：将size定义成全局变量，每次调用函数前初始化size

//求二叉树节点个数
int TreeSize(TreeNode* root)
{static int size = 0;if (root == NULL){return 0;}size++;TreeSize(root->left);TreeSize(root->right);return size;}

正确的定义与调用

#include<stdio.h>
#include<stdlib.h>
int size = 0;//快速构建一棵二叉树
typedef int DataType;
typedef struct TreeNode
{struct TreeNode* left;struct TreeNode* right;DataType data;
}TreeNode;//创建节点
TreeNode* BuyNode(DataType x)
{TreeNode* newnode = (TreeNode*)malloc(sizeof(TreeNode));if (newnode == NULL){perror("malloc fail");exit(-1);}newnode->data = x;newnode->left = NULL;newnode->right = NULL;return newnode;
}//快速构建一棵树
TreeNode* CreateBinaryTree()
{TreeNode* n1 = BuyNode(1);TreeNode* n2 = BuyNode(2);TreeNode* n3 = BuyNode(3);TreeNode* n4 = BuyNode(4);TreeNode* n5 = BuyNode(5);TreeNode* n6 = BuyNode(6);n1->left = n2;n1->right = n4;n2->left = n3;n2->right = NULL;n3->left = NULL;n3->right = NULL;n4->left = n5;n4->right = n6;n5->left = NULL;n5->right = NULL;n6->left = NULL;n6->right = NULL;return n1;
}
//求二叉树节点个数
int TreeSize(TreeNode* root)
{if (root == NULL){return 0;}size++;TreeSize(root->left);TreeSize(root->right);return size;}int main()
{TreeNode* root = CreateBinaryTree();printf("%d\n", TreeSize(root));size = 0;//初始化sizeprintf("%d\n", TreeSize(root));return 0;
}

转换成子问题：一棵二叉树节点的个数 = 左子树节点的个数+右子树节点的个数+1

左子树和右子树节点的个数也是其对于的左右子树节点个数之和+1

int TreeSize(TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

这种求解方法避免了定义变量的问题 

4.求二叉树中的叶子节点个数

求一棵树中叶子节点的个数，首先要清楚如何判断一个节点为叶子节点：

一个叶子节点的左右孩子都为空

求解叶子节点的个数问题也可以转换成子问题，一棵树中的叶子节点的个数为左子树中叶子节点的个数+右子树中叶子节点的个数 

//二叉树叶子节点的个数
int TreeLeafSize(TreeNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

5.求二叉树的高度

求解二叉树高度的问题转换成子问题：一棵树的高度 = max{左子树高度，右子树高度}+1

//二叉树的高度
int TreeHeight(TreeNode* root)
{if (root == NULL){return 0;}int left = TreeHeight(root->left);int right = TreeHeight(root->right);return  left > right ? left + 1 : right + 1;}

6.求二叉树第k层节点个数

求一棵树的第k层节点的个数转换成子问题：一棵树第k层节点的额个数 = 左子树第k-1层节点个数+右子树第k-1层节点个数

//二叉树第k层节点的个数
int TreeKLevel(TreeNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}k = k - 1;return TreeKLevel(root->left, k) + TreeKLevel(root->right, k);}

7.二叉树查找值为x的节点

查找值为x的节点转换成子问题：先检查根节点是否符合条件，不符合条件再去左子树找，左子树没找到去右子树查找，右子树没找到则返回NULL，载其中任何一个环节中如果中找到值为x的节点，则返回

//二叉树查找值为x的节点
TreeNode* TreeFind(TreeNode* root, int x)
{if(root == NULL){return NULL;}if (root->data == x){return root;}//在左子树查找TreeNode* ret = TreeFind(root->left, x);if (ret){return ret;}//左子树没找到，再在右子树查找ret = TreeFind(root->right, x);if (ret){return ret;}//整棵树都没找到return NULL;
}

 8.单值二叉树

单值二叉树题目链接：. - 力扣（LeetCode）

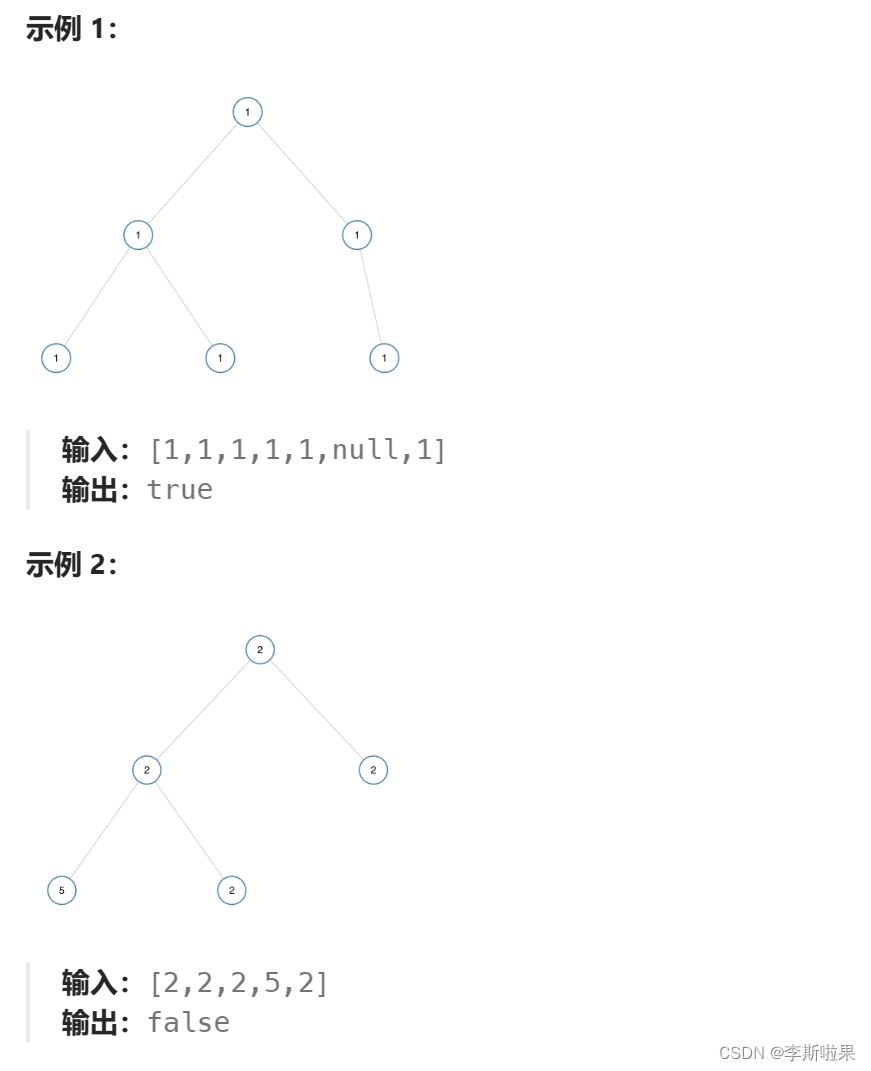
题目分析：

对于一棵单值二叉树，当其根节点的值等于左右孩子的值时，问题就可以转换成子问题，判断它的左右子树是否为单值二叉树，其左右子树的判断又重复之前的操作

📖Note：

对于一个节点，可能存在四种情况：

  • 有左右孩子
  • 只有左孩子
  • 只有右孩子
  • 没有孩子（叶子节点）

有左孩子节点时，父节点与左孩子节点比较，不相等返回false，相等则比较父节点与右孩子节点，不相等则返回false，相等则返回true

bool isUnivalTree(struct TreeNode* root) {if (root == NULL){return true;}//有左右孩子if (root->left && root->left->val != root->val){return false;}if (root->right && root->right->val != root->val){return false;}return isUnivalTree(root->left) && isUnivalTree(root->right);
}

9.二叉树最大深度

二叉树最大深度：. - 力扣（LeetCode）

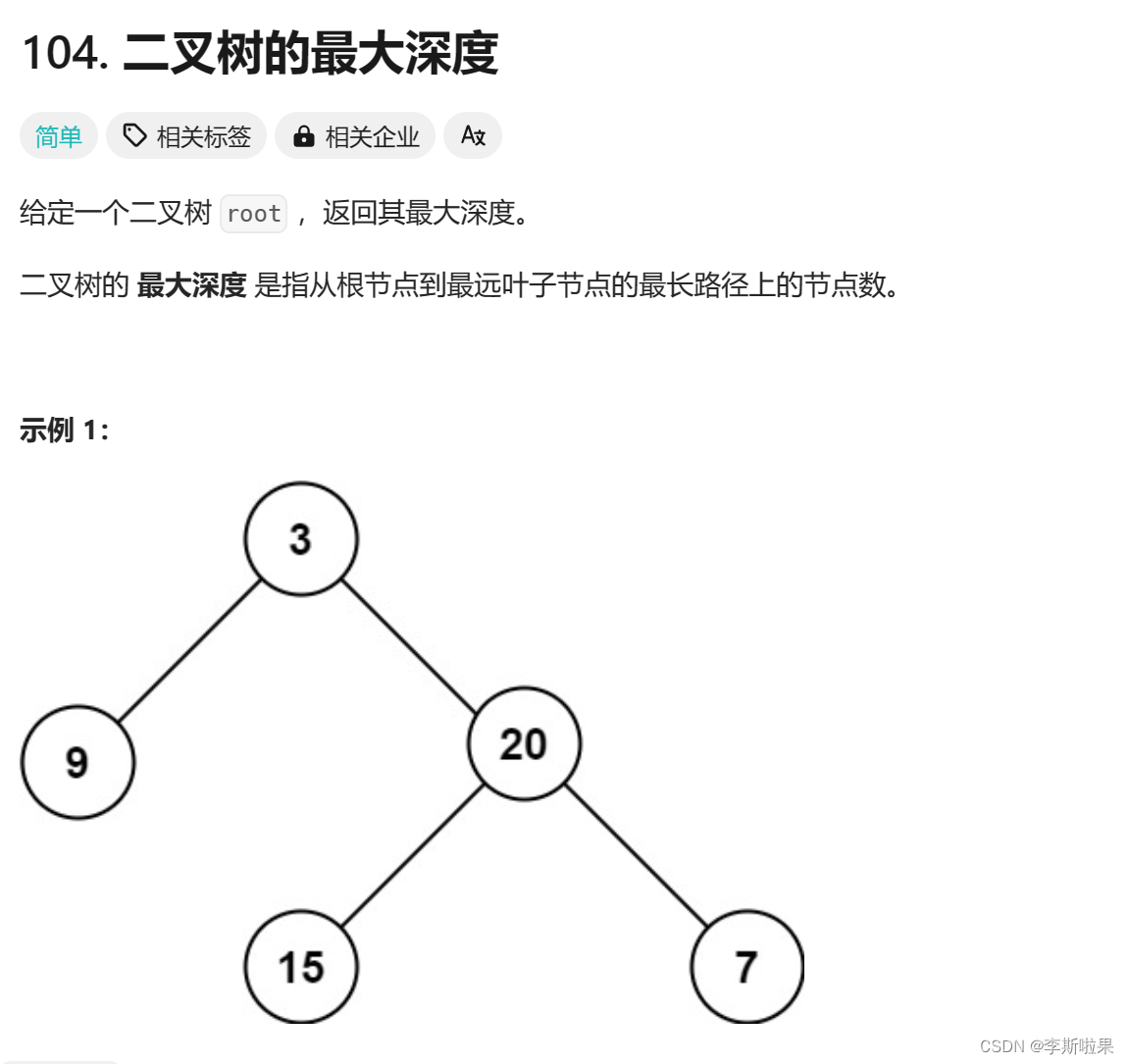
题目分析：

当二叉树为空时，其最大深度为0

当二叉树不为空时，求二叉树的最大深度转换成子问题为1加左右子树中深度较大者

int maxDepth(struct TreeNode* root) {if(root == NULL){return 0;}int leftmax = maxDepth(root->left);int rightmax = maxDepth(root->right);return  leftmax > rightmax ? leftmax + 1 : rightmax + 1;
}

10.翻转二叉树

翻转二叉树题目链接：226. 翻转二叉树 - 力扣（LeetCode）

题目分析：

翻转二叉树有两种方法

1️⃣使用递归实现

先序遍历二叉树的框架：先交换根节点的左右子树，再分别递归左子树右子树，即可实现二叉树的翻转

struct TreeNode* invertTree(struct TreeNode* root) {if (root == NULL){return root;}//交换左右子树struct TreeNode* tmp = root->left;root->left = root->right;root->right = tmp;invertTree(root->left);invertTree(root->right);return root;
}

2️⃣层序遍历法

层序遍历法基于队列实现

从根节点开始，层序遍历二叉树，依次翻转每一个节点的左右子树

struct TreeNode* invertTree(struct TreeNode* root)
{Queue q;QueueInit(&q);//根节点入队if (root){QueuePush(&q, root);}//队列不为空时while (!QueueEmpty(&q)){//访问队头元素并交换其左右子树struct TreeNode* front = QueueFront(&q);QueuePop(&q);struct TreeNode* tmp = front->left;front->left = front->right;front->right = tmp;//队头元素的孩子节点入队if (front->left){QueuePush(&q, front->left);}if (front->right){QueuePush(&q, front->right);}}return root;QueueDestroy(&q);
}

11. 检查两颗树是否相同

检查两颗树是否相同题目链接：. - 力扣（LeetCode）

题目分析：

两棵二叉树相同，不仅结构上相同，而且对应节点的值相同

1️⃣对于两颗空二叉树，则它们是相同的树

2️⃣对于一颗空树和一颗非空树，它们是不相同的树

3️⃣对于两颗非空树，先判断它们根节点的值是否相同，不相同则它们是不相同的树，相同则转换成子问题：依次比较它们的左右子树。当左右子树都相同时它们为相同的树

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//都为空树if (p == NULL && q == NULL){return true;}//一个空树一个非空树if (p == NULL || q == NULL){return false;}//两个非空树if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

12. 对称二叉树

对称二叉树题目链接：. - 力扣（LeetCode）

题目分析：

1️⃣对于一颗空树和只有一个节点的树，其为对称的树

2️⃣对于不止一个节点的树，如果其为对称的树，则其右子树翻转后和左子树是相同的树，这里需要用到我们已经写过的翻转二叉树和判断相同的树的函数

 //相同的二叉树
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//都为空树if (p == NULL && q == NULL){return true;}//一个空树一个非空树if (p == NULL || q == NULL){return false;}//两个非空树if (p->val != q->val){return false;}return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);}
//翻转二叉树
struct TreeNode* invertTree(struct TreeNode* root) {if (root == NULL){return root;}//交换左右子树struct TreeNode* tmp = root->left;root->left = root->right;root->right = tmp;invertTree(root->left);invertTree(root->right);return root;
}
//对称二叉树
bool isSymmetric(struct TreeNode* root) {//空树if (root == NULL){return true;}//只有一个节点的树if (root->left == NULL && root->right == NULL){return true;}//有左右孩子,且左右孩子为相同的树invertTree(root->right);return isSameTree(root->left,root->right);
}

13. 另一颗树的子树

另一颗树的子树题目链接：572. 另一棵树的子树 - 力扣（LeetCode）

 

题目分析：

1️⃣当一棵树为空时，任何树都不是其子树

2️⃣特殊情况：两棵树相同时，一颗是另一颗的子树

3️⃣当两棵树不相同时，递归判断主树的左子树与右子树是否与已知子树相同，只要左子树或右子树中存在与已知子树相同的树，则已知子树为主树的子树

//另一棵树的子树
bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if (root == NULL){return false;}if (isSameTree(root,subRoot)){return true;}return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

14.二叉树的前序遍历

二叉树的前序遍历题目链接：144. 二叉树的前序遍历 - 力扣（LeetCode）

​

题目分析：

本题的前序遍历不是单纯的打印，而是通过函数接口返回一个前序遍历序列数组（该数组是动态开辟的）

首先，要动态开辟数组，我们需要知道要开辟数组的大小，即二叉树节点的个数，调用题目3的函数接口TreeSize即可

然后，先序遍历二叉树，将二叉树节点按先序遍历的顺序依次存入我们动态开辟的数组，返回数组首元素地址即可

📖Note：

这里我们需要对先序遍历二叉树的函数接口增加一个参数，整型指针pi，用来指示每次存储的数组下标。如果在PreOrder函数内定义下标指针，每次递归都会使其初始化为0，所以采用参数的形式定义。

//求二叉树节点个数
int TreeSize(struct TreeNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//二叉树的前序遍历
void PreOrder(struct TreeNode* root, int* a, int* pi)
{if (root == NULL){return;}//static int i = 0;a[*pi] = root->val;printf("a[%d] = %d\n", pi, a[*pi]);++(*pi);PreOrder(root->left, a, pi);PreOrder(root->right, a, pi);
}//二叉树的前序遍历，返回序列数组
int* preorderTraversal(struct TreeNode* root, int* returnSize) {//开辟数组空间int n = TreeSize(root);//printf("%d\n",n);int* a = (int*)malloc(sizeof(int) * n);int i = 0;PreOrder(root, a, &i);*returnSize = n;return a;
}

15.通过前序遍历的数组构建二叉树 

 题目链接：二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

题目分析：

对已知字符串序列进行遍历，遇到空节点（#代表空节点）则访问下一个，需要对非空节点开辟空间并为其数据域赋值，递归构造左子树和右子树即可

#include <stdio.h>
#include<stdlib.h>typedef char BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;
//由前序序列构造二叉树
BTNode* BinaryTreeCreate(BTDataType* a,int* pi)
{if(a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if(root == NULL){perror("malloc fail\n");return NULL;}root->data = a[*pi];(*pi)++;root->left = BinaryTreeCreate(a, pi);root->right = BinaryTreeCreate(a, pi);return root;
}
//中序遍历
void InOrder(BTNode* root)
{if(root == NULL){return;}InOrder(root->left);printf("%c ",root->data);InOrder(root->right);
}int main() {char str[100];scanf("%s", str);int i = 0;BTNode* root = BinaryTreeCreate(str, &i);InOrder(root);return 0;
}

16.判断二叉树是否是完全二叉树

一颗完全二叉树可能为满二叉树，也可能非满，此时最后一层的节点连续排列

判断方法：层序遍历二叉树，将所有节点依次入队，再依次出队，遇到NULL，则跳出循环，判断后续队列中是否存在非空节点，不存在则为完全二叉树，否则为非完全二叉树。

//判断一棵树是否为完全二叉树
int BinaryTreeComplete(TreeNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q,root);}//节点入队while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q, root->left);QueuePush(&q, root->right);}//判断后续队列中是否有非空节点，有则不是完全二叉树while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);//存在非空元素if (front != NULL){QueueDestroy(&q);return false;}}QueueDestroy(&q);return true;
}

17.判断二叉树是否是平衡二叉树 

平衡二叉树题目链接：110. 平衡二叉树 - 力扣（LeetCode）

 

题目分析：

对于一颗空树和只有一个节点的树，其为平衡二叉树

平衡二叉树定义为：一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1

因此判断每个节点的左右左子树的高度差，调用题目9中二叉树的高度计算函数maxdepth

//二叉树的最大高度
int maxDepth(struct TreeNode* root) {if (root == NULL){return 0;}int leftmax = maxDepth(root->left);int rightmax = maxDepth(root->right);return  leftmax > rightmax ? leftmax + 1 : rightmax + 1;
}//平衡二叉树
bool isBalanced(struct TreeNode* root) {if (root == NULL){return true;}if (root->left == NULL && root->right == NULL){return true;}int left_heigh = maxDepth(root->left);int right_heigh = maxDepth(root->right);if (left_heigh - right_heigh == -1 || left_heigh - right_heigh == 0 || left_heigh - right_heigh == 1){if(isBalanced(root->left) && isBalanced(root->right))return true;}return false;
}

18.二叉树销毁  

1️⃣对于一颗空树，直接返回即可

2️⃣对于一颗只有一个节点的树，直接释放该节点所占用的空间

3️⃣二叉树的销毁转换成分治子问题：采用后续遍历二叉树的框架，对每一个节点，先释放左子树所占用的空间，再释放右子树所占用的空间，最后释放根节点所占用的空间

//二叉树的额销毁
void BinaryTreeDestroy(TreeNode* root)
{if (root == NULL){return;}BinaryTreeDestroy(root->left);BinaryTreeDestroy(root->right);free(root);
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/618846.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

NetDevOps：华三交换机通过Netmiko或者Nornir获取接口信息通过TextFSM解析报错问题

NetDevOps：华三交换机通过Netmiko或者Nornir获取接口信息通过TextFSM解析报错问题

python代码&#xff1a;实现功能获取交换机接口信息并通过TextFSM进行解析。 from netmiko import Netmiko import textfsm show_intf_cmd_mapping {hp_comware: display interface, }def ssh_device_2_get_intfs(device_type, host, username, password, port):dev_info {d…
阅读更多...
【2023年度回顾】让我们在新的一年继续努力前行

【2023年度回顾】让我们在新的一年继续努力前行

每当我们在努力的时候都会想&#xff1a;为什么我要努力&#xff1f;躺着不舒服吗&#xff1f; 大家好&#xff01;我是命运之光&#xff0c;一名普普通通的计算机科学与技术专业的大三学生。 &#x1f4d5;回顾一下整个2023年 因为我有每天发朋友圈的习惯&#xff0c;所以这一…
阅读更多...
chromedriver 114以后版本下载地址

chromedriver 114以后版本下载地址

谷歌浏览器版本经常会升级&#xff0c;chromedriver 也得下载匹配的版本 chromedriver 114以前版本下载地址https://registry.npmmirror.com/binary.html?pathchromedriver/ 找到匹配浏览器版本 查看自己浏览器版本号v120.0 v120.0版本chromedriver下载地址https://google…
阅读更多...
Ubuntu 22.04 安装prometheus

Ubuntu 22.04 安装prometheus

服务器监控和报警软件有很多&#xff0c;为什么我们会选择Prometheus而不是其他软件呢&#xff1f; 因为它有以下优点&#xff1a; 自带简易web监控页面&#xff0c;用户可以很方便地查看监控数据和使用仪表盘。能实时收集数据并根据自定义警报规则推送告警&#xff1b;具有丰…
阅读更多...
Java SPI在数据库驱动、SpringBoot自动装配中的应用

Java SPI在数据库驱动、SpringBoot自动装配中的应用

文章目录 1. 初识SPI1.1 SPI的作用1.2 SPI的工作原理1.3 SPI的三个组件&#xff1a;Service、Service Provider、ServiceLoader1.4 SPI使用场景1.5 具体的SPI 源码分析&#xff08;SPI的核心就是ServiceLoader.load()方法&#xff09;1.6 SPI 的优缺点 2. API、SPI、JNDI释义3.…
阅读更多...
uniapp滑动页面切换和下拉刷新，触底加载更多（swiper + scroll-view）

uniapp滑动页面切换和下拉刷新，触底加载更多（swiper + scroll-view）

因为官方文档乱七八糟的&#xff0c;所以自己来总结下 需求&#xff1a; 常见的上方tag标签切换&#xff0c;下方是页面&#xff0c;上面点击切换&#xff0c;下面页面也切换&#xff0c;下方列表有下拉刷新&#xff0c;触底加载更多 因为这两个组件都是固定高度的&#xff0c;…
阅读更多...
6.2 声音编辑工具GoldWave5简介(6)

6.2 声音编辑工具GoldWave5简介(6)

3&#xff0e;选择【选项】|【控制器属性】命名或单击“控制器”面板上的“设置控制器属性”按钮&#xff0c;打开“控制器属性”对话框&#xff0c;将“音量”选项卡中的“麦克风”选项打上勾&#xff0c;使GoldWave只能录制来自麦克风的声音。如果要录制电脑内部的声音&#…
阅读更多...
聊天机器人之接收实时信息实现（二）

聊天机器人之接收实时信息实现（二）

准备工作 如果没有准备好环境的请看 前期环境准备 这里默认已经注入成功并且已经登录好了账号。 具体实现 实现原理 通过本地搭建一个web服务&#xff0c;来接收一个POST请求&#xff0c;这个请求中就会涵盖实时的数据&#xff0c;包括昵称、消息内容、消息类型之类的。 p…
阅读更多...
Head First Design Patterns -工厂模式

Head First Design Patterns -工厂模式

什么是工厂模式 工厂方法模式定义了一个创建对象的接口&#xff0c;但由子类来决定要实例化那个类。工厂方法让类把实例化推迟到了子类。 为什么要有工厂模式 书中以pizza店制作pizza为例子&#xff0c;假设不用工厂模式&#xff0c;在制作pizza阶段我们需要这样去实例化类&am…
阅读更多...
回声状态网络（Echo State Networks,ESN）详细原理讲解及Python代码实现

回声状态网络（Echo State Networks,ESN）详细原理讲解及Python代码实现

回声状态网络&#xff08;Echo State Networks,ESN&#xff09;详细讲解及Python代码实现 1 基本概念 回声状态网络是一种循环神经网络。ESN 训练方式与传统 RNN 不同。网络结构如下图&#xff1a; &#xff08;1&#xff09;储层&#xff08;Reservoir&#xff09;&#x…
阅读更多...
vue中使用js-doc

vue中使用js-doc

安装依赖 安装vue-template-compiler npm install ​vue-template-compiler​npm install ​vue-template-compiler​ 安装minami npm install minami 安装js-doc npm install js-doc 根目录下创建 .jsdoc.conf.json 内容&#xff1a; {"tags": {"all…
阅读更多...
在Linux中创建文件的多种方法

在Linux中创建文件的多种方法

目录 前言1 使用重定向符号 ">"2 使用文本编辑器 vi/vim3 使用 nano4 使用 echo5 使用 touch6 使用 printf7 使用 head8 使用 cat9 使用 tail10 使用 truncate结语 前言 在Linux系统中&#xff0c;文件的创建是日常操作中不可避免的一部分。无论是创建空文件、编…
阅读更多...
解决MPICH的GPU初始化失败：一次深入探索

解决MPICH的GPU初始化失败：一次深入探索

今天来分享“MPICH&#xff1a;MPII_Init_thread(222): gpu_init failed”这个问题的解决方式 文章目录 前言问题原因解决方案 前言 如果在安装MPICH的时候没有注意要一些选项&#xff0c;那么当使用mpicxx mpi_send.cpp -o send && mpirun -n 2 ./send进行编译输出的…
阅读更多...
图片特效/增强GUI程序

图片特效/增强GUI程序

程序下载地址&#xff1a;mendianyu/pictureConvert: 图片特效/增强GUI程序&#xff0c;借助百度接口实现人像动漫化&#xff0c;模糊图片变清晰等等功能 (github.com) 图片特效/增强GUI程序 借助百度接口实现人像动漫化&#xff0c;模糊图片变清晰等等功能 程序介绍 运行Ima…
阅读更多...
LIS系统：样本采集、检验、分析、查看报告

LIS系统：样本采集、检验、分析、查看报告

检验科LIS系统是实验室信息管理系统&#xff0c;主要用于实验室检验工作流程管理、病人信息管理、检验结果查询、统计和报表打印等功能。它采用智能辅助功能&#xff0c;自动接收检验数据、打印检验报告&#xff0c;并保存检验信息的工具。同时&#xff0c;可根据实验室需要实现…
阅读更多...
opencv(C++)基础用法

opencv(C++)基础用法

文章目录 前言一、opencv (C)图片基本操作1.1 读取图片并显示1.2 颜色转换1.3 图像filtering1.4 形状调整1.5 绘制 二、读取视频文件并显示三、RTSP 视频流四. 人脸检测总结 前言 学习笔记 一、opencv (C)图片基本操作 1.1 读取图片并显示 #include "opencv2/opencv.hp…
阅读更多...
二、Java中SpringBoot组件集成接入【MySQL和MybatisPlus】

二、Java中SpringBoot组件集成接入【MySQL和MybatisPlus】

二、Java中SpringBoot组件集成接入【MySQL和MybatisPlus】 1.MySQL和MybatisPlus简介2.maven依赖3.配置1.在application.yaml配置中加入mysql配置2.新增Mybatis-Plus配置类 4.参考文章 1.MySQL和MybatisPlus简介 MySQL是一种开源的关系型数据库管理系统&#xff0c;被广泛应用…
阅读更多...
Python——猜猜心里的数字（1）

Python——猜猜心里的数字（1）

首先呢&#xff0c;我们自定义一个数字&#xff0c;然后让对方猜一猜是否能猜中&#xff0c;接下来我们以10为例&#xff0c;给对方三次机会。 num10 if int(input("请猜一个数字:"))num:print("恭喜第一次就猜对了") elif int(input("猜错了&#x…
阅读更多...
每日一题——LeetCode1128.等价多米诺骨牌对的数量

每日一题——LeetCode1128.等价多米诺骨牌对的数量

先尝试暴力解法&#xff1a; var numEquivDominoPairs function(dominoes) {var count0for(let i0;i<dominoes.length-1;i){for(let ji1;j<dominoes.length;j){if((dominoes[i][0]dominoes[j][0] && dominoes[i][1]dominoes[j][1]) || (dominoes[i][0]dominoes…
阅读更多...
Mac下载Navicat premium提示文件损坏的解决方案

Mac下载Navicat premium提示文件损坏的解决方案

引用&#xff1a;https://blog.csdn.net/weixin_44898291/article/details/120879508 sudo xattr -r -d com.apple.quarantine
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023