1.题目分析：

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

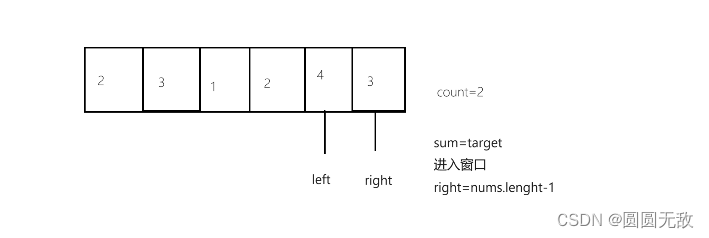
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 
[4,3]是该条件下的长度最小的子数组。

1.找出连续子数组

2.最短长度

3.特殊情况：数组总和小于target，返回零

 2.算法分析：

方法一：暴力枚举：时间复杂度是O(n^3)

设置两个指针，分别表示子数组的开始和子数组的结束两层for循环，最后求子数组总和一个while，自己在脑子想想，跑不过，我就不画图，写代码了哈。

方法二：在暴力枚举的方法上做出改进-->滑动窗口，还是用了双指针，和单调性，全是正数会越加越大，让两个指针同向移动来实现优化

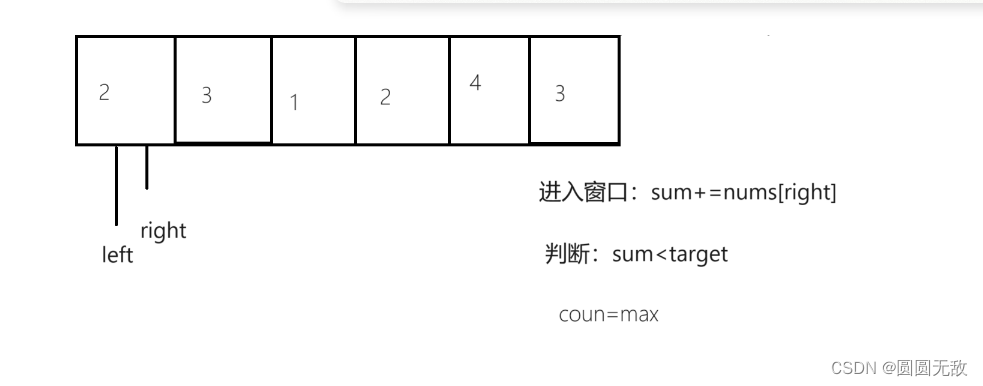
滑动窗口步骤：1.进入窗口

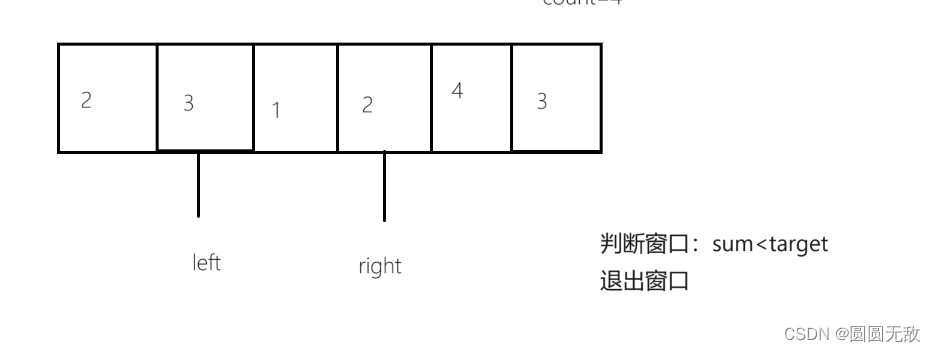
                         2.判断窗口

                         3.退出窗口

 例一图示（target = 7, nums = [2,3,1,2,4,3]）：

 

 

 

 

 

 

3.代码编写：

public static int minSubArrayLen(int target, int[] nums) {int sum=0;int count=Integer.MAX_VALUE;int left=0;int right=0;for(left=0,right=0;right<nums.length;right++){sum+=nums[right];//进窗口while (sum>=target)//判断{count=Math.min(count,right-left+1);sum-=nums[left++];//出窗口}}if(count==Integer.MAX_VALUE){return 0;}return count;}