蓝桥杯
我的AcWing
题目及图片来自蓝桥杯C++ AB组辅导课
数论(上)
蓝桥杯省赛中考的数论不是很多,这里讲几个蓝桥杯常考的知识点。
欧几里得算法——辗转相除法
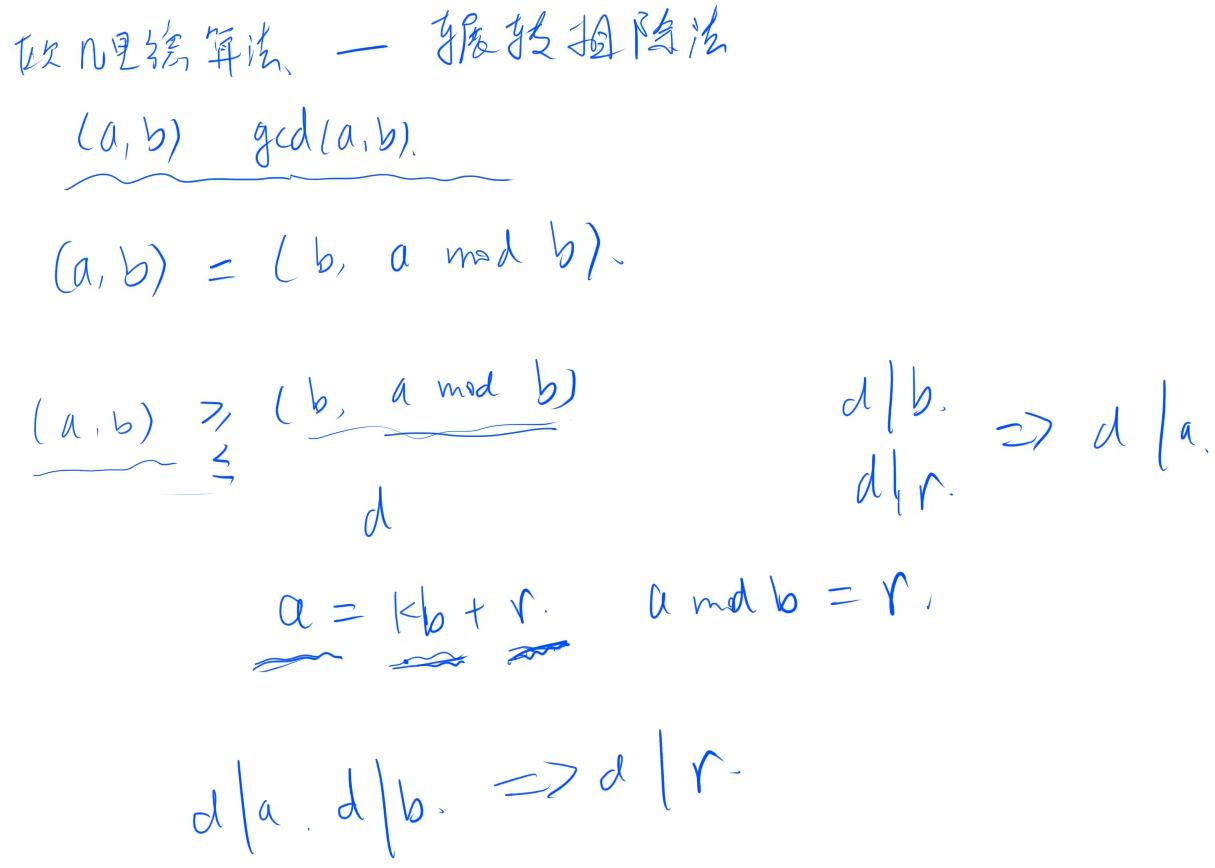
欧几里得算法代码:
import java.util.Scanner ;public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int a = sc.nextInt(), b = sc.nextInt();System.out.println(gcd(a, b));}private static int gcd(int a, int b) {return b != 0 ? gcd(b, a % b) : a;}
}
算术基本定理
就是因式分解的定理,所有的整数都可以唯一分解成若干个质因子乘积的形式:
N = P 1 α 1 × P 2 α 2 × . . . × P k α k N=P_{1}^{α_{1}}×P_{2}^{α_{2}}×...×P_{k}^{α_{k}} N=P1α1×P2α2×...×Pkαk,其中 P i P_{i} Pi 是质数,每一个 α i ≥ 0 α_{i} \geq0 αi≥0
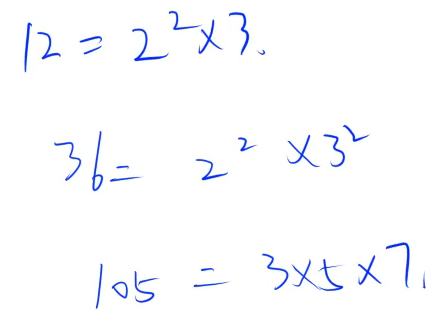
筛法求素数——线性筛法(欧拉筛法)
在 O ( N ) O(N) O(N)的时间复杂度内,求出来1 ~ n中所有的质数,以及每一个数的最小质因子。
import java.util.Scanner ;public class Main {static final int N = 1000010;static int[] primes = new int[N]; // 存所有的质数static int cnt; // 存质数的个数static boolean[] st = new boolean[N]; // 当前数有没有被筛过 0没有被筛过 1表示筛过public static void main(String[] args) {get_primes(100000);for (int i = 0; i < 20; i++) System.out.println(primes[i]); // 输出100000的前20个质数}private static void get_primes(int n) {for (int i = 2; i <= n; i++) {if (!st[i]) primes[cnt++] = i;for (int j = 0; primes[j] * i <= n; j++) {/*因为prime中素数是递增的,所以如果i%prime[j]!=0代表i的最小质因数还没有找到,即i的最小质因数大于prime[j]也就是说prime[j]就是i*prime[j]的最小质因数,于是i*prime[j]被它的最小质因数筛掉了*/st[primes[j] * i] = true; // 把质数的i倍筛掉/*如果当i%prime[j]==0时,代表i的最小质因数是prime[j],那么i*prime[j+k](k>0)这个合数的最小质因数就不是prime[j+k]而是prime[j]了所以i*prime[j+k]应该被prime[j]筛掉,而不是后续的prime[j+k],于是在此时break*/if (i % primes[j] == 0) break; // 通过最小质因子来筛}}}
}
注释中的两段解释参考博客 线性筛(欧拉筛)——算法解析
① 筛掉的一定是合数,且一定是用其最小质因子筛的
② 合数一定会被筛掉

这样我们就可以把所有质数找出来,而且每个和数只会被最小质因子筛,所以每个和数只会被筛一次,所以整个算法的时间复杂度为 O ( N ) O(N) O(N)
例题
AcWing 1295. X的因子链
算术基本定理
线性筛法
题意有点绕,通俗来讲就是给我们任意一个正整数 X X X,我们可以求一下 X X X所有的约数: d 1 , d 2 . . . d k d_{1},d_{2}...d_{k} d1,d2...dk,然后我们要从中挑出来一些严格单调递增的数,使得每一项都是它前一项的倍数: a 1 < a 2 < . . . < a t a_{1}<a_{2}<...<a_{t} a1<a2<...<at ( a i ∣ a i + 1 ) (a_{i}|a_{i+1}) (ai∣ai+1),然后问我们可以挑出来的序列的最大长度是多少,以及有多少个满足条件的单调递增的序列?
每一项必然满足: a i + 1 = a i ⋅ P ( P 是倍数且 > 1 ) a_{i+1} = a_{i}·P(P是倍数 且>1) ai+1=ai⋅P(P是倍数且>1),每一个后一项都等于前一项乘上一个倍数,那么我们要想让整个序列最长的话,要尽可能让倍数最小,最小只能小到质数,因为小到质数就不能再分了,因此就可以用我们上边的算术基本定理了,假设 X X X分解质因数的结果: X = P 1 α 1 × P 2 α 2 × . . . × P k α k X=P_{1}^{α_{1}}×P_{2}^{α_{2}}×...×P_{k}^{α_{k}} X=P1α1×P2α2×...×Pkαk,我们可以发现一共有 α 1 + α 2 + . . . + α k α_{1}+α_{2}+...+α_{k} α1+α2+...+αk 个质因子,因此我们每一次后一项要比前一项至少要多一个倍数,每一次的倍数必然是一个质数,必然是在 X X X当中的某一个质因子,所以序列的最大长度就是 α 1 + α 2 + . . . + α k α_{1}+α_{2}+...+α_{k} α1+α2+...+αk
那么如何求这样序列的个数呢?先做一个映射,我们不存数的本身,我们存数的增量,原序列是 a 1 , a 2 . . . a t a_{1},a_{2}...a_{t} a1,a2...at,映射的序列是: a 1 a_{1} a1, a 2 a 1 a_{2}\over a_{1} a1a2, a 3 a 2 a_{3}\over a_{2} a2a3 . . . ... ... a t a t − 1 a_{t}\over a_{t-1} at−1at,这两个序列是一一对应的,给我们第一个序列就可以求第二个序列,在第二个序列中每一个数都是 X X X的质因子,因此序列个数就是 X X X所有质因子的排列数。

排列数公式: ( α 1 + α 2 + . . . + α k ) ! α 1 ! ⋅ α 2 ! ⋅ . . . ⋅ α k ! (α_{1}+α_{2}+...+α_{k})! \over α_{1}!·α_{2}!·...·α_{k}! α1!⋅α2!⋅...⋅αk!(α1+α2+...+αk)!,也被称为多重集合的排列数问题,这样就避免了重复情况。
我们分解质因数就用线性筛法来解。
import java.util.Scanner ;public class Main {static final int N = (1 << 20) + 10;static int[] primes = new int[N]; // 存所有的质数static int cnt; // 存质数的个数static int[] minp = new int[N]; // 存最小质因子static boolean[] st = new boolean[N]; // 当前数有没有被筛过public static void main(String[] args) {Scanner sc = new Scanner(System.in);get_primes(N - 1);int[] fact = new int[30]; // 记录因子int[] sum = new int[N]; // 存因子个数while (sc.hasNext()) {int x = sc.nextInt();int k = 0, total = 0;while (x > 1) {int p = minp[x];fact[k] = p;sum[k] = 0;while (x % p == 0) { // 分解质因数x /= p;sum[k]++;total++;}k++;}long res = 1;for (int i = 1; i <= total; i++) res *= i; // 求total的阶乘for (int i = 0; i < k; i++) { // 多重集合的排列数for (int j = 1; j <= sum[i]; j++) {res /= j;}}System.out.println(total + " " + res);}}private static void get_primes(int n) {for (int i = 2; i <= n; i++) {if (!st[i]) {minp[i] = i; // 因为i是质数 最小质因子就是它本身primes[cnt++] = i;}for (int j = 0; primes[j] * i <= n; j++) {int t = primes[j] * i;st[t] = true;minp[t] = primes[j];st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}}
}
第十届2019年蓝桥杯真题
AcWing 1246. 等差数列
C++B组第8题
最大公约数
欧几里得算法
在等差数列中,每一项与第一项的差一定是公差d的倍数,但是题中的等差数列有一部分未连续,所以我们要找到除了第一项,其余的每一项和第一项的差的最大公约数d,d就是整个数列公差的最大值。
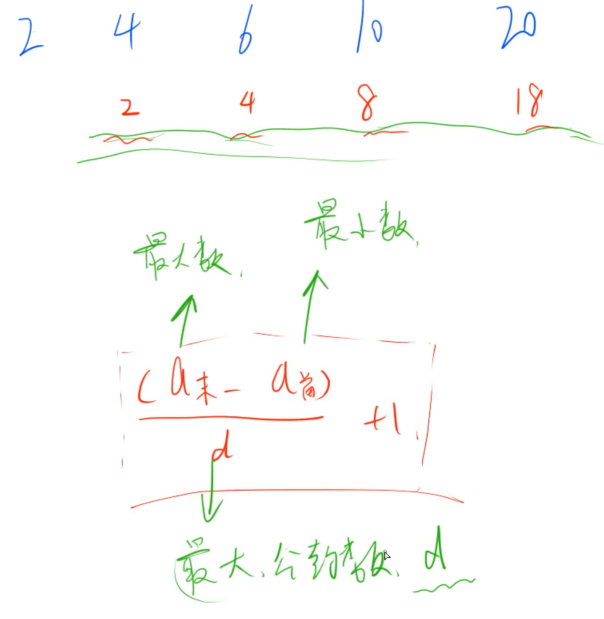
求项数公式: a 末 − a 首 d a_{末}-a_{首} \over d da末−a首 + 1 + 1 +1
时间复杂度 O ( N l o g N ) O(NlogN) O(NlogN)
import java.util.Scanner;
import java.util.Arrays;public class Main {static final int N = 100010;static int[] a = new int[N];public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt();for (int i = 0; i < n; i++) a[i] = sc.nextInt();Arrays.sort(a, 0, n);int d = 0;for (int i = 1; i < n; i++) d = gcd(d, a[i] - a[0]); // 求最大公约数if (d == 0) System.out.print(n); // 表示所有项都相同else System.out.print((a[n - 1] - a[0]) / d + 1); // 求项数公式}private static int gcd(int a, int b) {return b != 0 ? gcd(b, a % b) : a;}
}
第七届2016年蓝桥杯真题
AcWing 1223. 最大比例
C++B组第10题
最大公约数
辗转相减法
有 M M M个奖金构成了一个等比数列,奖金是正整数,但是比值有可能是分数;从这些等比数列挑出一部分数字,通过选出来的这些数来推断原来等比数列的比值的最大可能值是多少。

这题太难了,没肝动。



)








)

——物理验证)




