文章目录
- 引言
- 决策树学习基本思路
- 划分选择
- 信息熵
- 信息增益
- 增益率(C4.5)
- 基尼指数(CART)
- 剪枝处理
- 预剪枝(逐步构建决策树)
- 后剪枝(先构建决策树再剪枝)
- 连续值与缺失值处理
- 连续值处理
- 缺失值处理
- 结论
- 实验分析
引言
随着信息时代的发展,决策制定变得愈发复杂而关键。在众多决策支持工具中,决策树作为一种直观而强大的工具,在各个领域都得到了广泛的应用。决策树是一种基于树形结构的模型,通过一系列的决策节点和分支来模拟决策过程。其简洁的图形表示和易于理解的特性使其在商业、医疗、金融等领域取得了显著的成果。
决策树的核心思想是通过一系列有序的问题,逐步缩小决策空间,最终得出明确的结论。这种分层递归的方法不仅使得决策过程变得透明和可解释,同时也使得决策树模型适用于各种规模和类型的问题。从对客户购买行为的预测到医学诊断的辅助,决策树都展现了其在辅助决策制定方面的卓越能力。
在本文中,我们将深入探讨决策树的原理、构建方法以及在实际问题中的应用。我们将介绍决策树的基本结构、常用算法,并通过实例说明如何应用决策树解决现实生活中的复杂问题。通过深入了解决策树,读者将能够更好地理解其潜在价值,并在实践中灵活应用,以优化决策过程并取得更好的结果。
决策树学习基本思路
决策树学习的目的是为了产生一颗泛化能力强的决策树,其基本流程遵循“分而治之”策略。在决策树基本算法中,一共有三种情形会导致递归的返回:
- 当前结点包含的样本全属于同一类别,无需划分。
- 当前属性集为空,或是所有样本在所有属性上取值相同,无法划分。
- 当前结点包含的样本集合为空,不能划分。
算法基本流程如下所示:
Input:训练集 D={(x1,y1),(x2,y2),...,(xm,ym)}属性集 A={a1,a2,...,ad}
过程:函数 TreeGenerate(D,A)生成结点 node;
if D中的每一个样本全属于同一类别C将node标记为C类的叶子结点; return
end ifif A=ø or D中的样本在A上取值相同将node标记为叶结点,其类别标记为D中样本数最多的类; return
end if从A中选择最优划分属性a;
for a 的每一个值 av为node生成一个分支;令Dv表示D中在a上取值为av的样本子集;if Dv为空将分支结点标记为叶结点,其类别标记为D中样本最多的类; returnelse以 TreeGenerate(Dv,A\{a}) 为分支结点end if
end forOutput:以node为根节点的一颗决策树
划分选择
显然如何选择划分属性是决策树学习的关键。一般而言,随着划分过程不断进行,希望决策树的分支结点所包含的样本尽可能属于同一类别,即结点的纯度越高越好。
信息熵
信息熵是度量样本集合纯度最常用的一种指标。假定当前样本集合 D D D中第 k k k类样本所占的比例为 p k ( k = 1 , 2 , . . . , ∣ y ∣ ) p_k(k=1,2,...,|y|) pk(k=1,2,...,∣y∣),则 D D D的信息熵定义为:
E n t ( D ) = − ∑ k = 1 ∣ y ∣ p k l o g 2 p k Ent(D)=-\sum_{k=1}^{|y|}p_klog_2p_k Ent(D)=−k=1∑∣y∣pklog2pk
其中, ∣ y ∣ |y| ∣y∣表示类别的总数。信息熵的值越小,表示样本集合的纯度越高。当信息熵为0时,样本集合中只包含一类样本,纯度最高;而当信息熵达到最大值 l o g 2 ∣ y ∣ log_2|y| log2∣y∣时,表示样本集合中的各类样本均匀混合,纯度最低。信息熵的背景是衡量在划分样本集合时还需要多少信息,才能使得划分后的子集合更加纯净。
信息增益
信息增益用于衡量选择某个特征进行分裂后,对数据集信息熵的减少程度。选择具有最大信息增益的特征作为节点的分裂特征。信息增益的计算公式如下:
G a i n ( D , a ) = E n t ( D ) − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ E n t ( D v ) Gain(D,a)=Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v) Gain(D,a)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
其中 E n t ( D ) Ent(D) Ent(D)表示数据集 D D D的信息熵。 ∣ D v ∣ |D^v| ∣Dv∣表示在特征 a a a上取值为 v v v的样本子集的大小。 ∣ D ∣ |D| ∣D∣表示数据集 D D D的大小,即样本集合的总样本数。 E n t ( D v ) Ent(D^v) Ent(Dv)表示在特征 a a a上取值为 v v v的样本子集的信息熵。
信息增益越大,表示选择该特征进行分裂后,数据集的纯度提高得越多,即更好地区分不同类别的样本。在决策树的学习过程中,会计算每个特征的信息增益,然后选择具有最大信息增益的特征作为节点进行分裂。这一过程不断递归,直到满足停止条件。
增益率(C4.5)
若过度的追求信息增益率,会使得模型的泛化能力差,无法对新的样本进行有效的预测。(ex:用编号作为属性)
C4.5是一种经典的决策树学习算法,不直接采用信息增益,而是使用“增益率”来选择划分属性,增益率的定义为
G a i n r a t i o ( D , a ) = G a i n ( D , a ) I V ( a ) Gain_{ratio}(D,a)=\frac{Gain(D,a)}{IV(a)} Gainratio(D,a)=IV(a)Gain(D,a)
其中
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ l o g 2 ∣ D v ∣ ∣ D ∣ IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
称为属性 a a a的固有值。属性 a a a的可能取值数目越多(即 V V V越大),则 I V ( a ) IV(a) IV(a)的值通常会越大。
需要注意的是,C4.5算法并不是直接选择增益率最大的候选划分属性,而是使用了一个启发式:先从候选划分属性中找出信息增益高于平均的属性,再从中选择增益率最高的。
基尼指数(CART)
CART是一种用于分类和回归问题的决策树学习算法,使用“基尼指数”来选择划分属性,数据集 D D D的纯度可用基尼值来度量:
G i n i ( D ) = 1 − ∑ k = 1 ∣ y ∣ p k 2 Gini(D)=1-\sum_{k=1}^{|y|}p_k^2 Gini(D)=1−k=1∑∣y∣pk2
其中 p k p_k pk表示数据集中第 k k k类样本的占比,直观来讲, G i n i ( D ) Gini(D) Gini(D)反映了从数据集 D D D中随机抽取两个样本,其类别标记不一致的概率。因此 G i n i ( D ) Gini(D) Gini(D)越小,则数据集 D D D的纯度越高。
属性 a a a的基尼指数定义为:
G i n i i n d e x ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ G i n i ( D v ) Gini_{index}(D,a)=\sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v) Giniindex(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)
基尼指数的取值范围在 [ 0 , 1 ] [0, 1] [0,1] 之间,当基尼指数越小时,表示数据集的纯度越高,即数据集中的样本越趋于属于同一类别。反之,当基尼指数较大时,表示数据集的混合程度较高,样本分布较为均匀。
在决策树的构建中,基尼指数常被用于选择最优的特征和切分点,以便在节点分裂时获得最大的纯度提升。选择基尼指数最小的划分方式意味着选择了最能够将不同类别样本分开的方式,即 a ⋆ = a r g a ∈ A m i n G i n i i n d e x ( D , a ) a_\star=arg_{a\in A} \ min \ Gini_{index}(D,a) a⋆=arga∈A min Giniindex(D,a)。
剪枝处理
在决策树中,剪枝是一种用于防止过拟合的主要技术,其目标是通过简化树的结构,提高模型的泛化性能。剪枝的过程通常分为预剪枝和后剪枝两种方式。
预剪枝(逐步构建决策树)
用验证集对单个结点决策树进行评估,分为划分前精度和划分后精度,通过比较若划分后精度 > > >划分前精度(奥卡姆剃刀原则),则预剪枝决策:划分。
在一方面预剪枝可以有效的降低过拟合风险,通过在构建树的过程中提前停止节点的分裂,避免生成过于复杂的树,有助于提高模型的泛化能力;减少计算开销,避免对于不必要的节点进行分裂和计算,从而减少了计算开销,提高了构建速度;简化模型: 预剪枝产生的树往往更简化,更容易理解和解释。但是另一方面预剪枝易造成信息的丢失, 提前停止节点的分裂可能导致模型在学习过程中丢失一些关键信息,特别是当真实决策边界比较复杂时;难以确定最优剪枝时机,选择不当可能导致模型性能下降;对噪声敏感,因为它提前停止了分裂,而无法充分利用真实的数据模式。
后剪枝(先构建决策树再剪枝)
后剪枝是先从训练集中生成一颗完整的决策树,然后自下而上进行剪枝操作。仍然使用验证集对单个结点决策树进行评估,分为划分前精度和划分后精度,通过比较若划分后精度 ≤ \leq ≤划分前精度(奥卡姆剃刀原则),则后剪枝决策:划分。
对于时间开销来讲:
- 预剪枝:测试时间开销降低,训练时间开销降低。
- 后剪枝:测试时间开销降低,训练时间开销增加。
过/欠拟合风险:
- 预剪枝:过拟合风险降低,欠拟合风险增加。
- 后剪枝:过拟合风险降低,欠拟合风险不变。
泛化能力: 后剪枝 > > >预剪枝。
连续值与缺失值处理
连续值处理
在现实学习任务中常常会遇到连续属性,我们有必要讨论如何在决策树学习中使用连续属性。
对于连续特征,可以考虑每两个相邻特征值 [ a i , a i + 1 ) [a^i,a^{i+1}) [ai,ai+1)的中点作为划分点,计算信息增益,选择使信息增益最大的划分点。
T a = { a i + a i + 1 2 ∣ 1 ≤ i ≤ n − 1 } T_a= \{\frac{a^i+a^{i+1}}{2}|1\leq i\leq n-1\} Ta={2ai+ai+1∣1≤i≤n−1}
我们就可以获得样本集 D D D基于划分点 t t t二分后的信息增益。
G a i n ( D , a ) = m a x ( t ∈ T a ) E n t ( D ) − ∑ λ ∈ ( − , + ) ∣ D t λ ∣ ∣ D ∣ E n t ( D t λ ) Gain(D,a)=max_{(t\in T_a)}\ Ent(D)-\sum_{\lambda \in {(-,+)}} \frac{|D_t^{\lambda}|}{|D|}Ent(D_t^{\lambda}) Gain(D,a)=max(t∈Ta) Ent(D)−λ∈(−,+)∑∣D∣∣Dtλ∣Ent(Dtλ)
缺失值处理
在现实任务中,我们常会遇到不完整的样本,即样本某些属性的缺失值。
我们需要解决两个问题:
- 如何在属性值缺失的情况下进行划分属性选择?
- 给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
给定训练集 D D D和属性 a a a,令 D ~ \tilde{D} D~表示 D D D中在属性 a a a上没有样本缺失值的样本子集。假定属性 a a a有 V V V个可取值 { a 1 , a 2 , . . . , a V } \{a^1,a^2,...,a^V \} {a1,a2,...,aV},令 D ~ v \tilde{D}^v D~v表示 D ~ \tilde{D} D~中在属性 a a a上取值为 a v a^v av的样本子集。 D ~ k \tilde{D}^k D~k表示 D ~ \tilde{D} D~中属于第 k k k类 { k = 1 , 2 , . . . , ∣ y ∣ } \{k=1,2,...,|y| \} {k=1,2,...,∣y∣}的样本子集,则显然有 D ~ = ⋃ k = 1 ∣ y ∣ D ~ k \tilde{D}=\bigcup_{k=1}^{|y|}\tilde{D}^k D~=⋃k=1∣y∣D~k, D ~ = ⋃ v = 1 V D ~ v \tilde{D}=\bigcup_{v=1}^{V}\tilde{D}^v D~=⋃v=1VD~v。假定我们赋予每个样本 x x x一个权重 w x w_x wx,并定义:
ρ = ∑ x ∈ D ~ w x ∑ x ∈ D w x \rho=\frac{\sum_{x \in \tilde{D}}w_x}{\sum_{x \in D}w_x} ρ=∑x∈Dwx∑x∈D~wx
p ~ k = ∑ x ∈ D ~ w x ∑ x ∈ D w x ( 1 ≤ k ≤ ∣ y ∣ ) \tilde{p}_k=\frac{\sum_{x \in \tilde{D}}w_x}{\sum_{x \in D}w_x} \quad (1\leq k\leq|y|) p~k=∑x∈Dwx∑x∈D~wx(1≤k≤∣y∣)
r ~ v = ∑ x ∈ D ~ w x ∑ x ∈ D w x ( 1 ≤ v ≤ V ) \tilde{r}_v=\frac{\sum_{x \in \tilde{D}}w_x}{\sum_{x \in D}w_x} \quad (1\leq v\leq V) r~v=∑x∈Dwx∑x∈D~wx(1≤v≤V)
其中对属性 a a a, ρ \rho ρ表示无缺失值样本所占的比例, p ~ k \tilde{p}_k p~k表示无缺失值样本中第 k k k类所占的比例, r ~ v \tilde{r}_v r~v表示无缺失值样本中在属性 a a a上取值为 a v a^v av的样本所占的比例。显然 ∑ k = 1 ∣ y ∣ p ~ k = 1 \sum_{k=1}^{|y|}\tilde{p}_k=1 ∑k=1∣y∣p~k=1, ∑ v = 1 V r ~ v = 1 \sum_{v=1}^{V}\tilde{r}_v=1 ∑v=1Vr~v=1。
基于上述定义,我们可以将信息增益的计算式推广为:
G a i n ( D , a ) = ρ × ( E n t ( D ~ ) − ∑ v = 1 V r ~ v E n t ( D ~ v ) ) Gain(D,a)=\rho \times (Ent(\tilde{D})-\sum_{v=1}^V\tilde{r}_vEnt(\tilde{D}^v)) Gain(D,a)=ρ×(Ent(D~)−v=1∑Vr~vEnt(D~v))
有
E n t ( D ~ ) = − ∑ k = 1 ∣ y ∣ p ~ k l o g 2 p ~ k Ent(\tilde{D})=-\sum_{k=1}^{|y|}\tilde{p}_klog_2\tilde{p}_k Ent(D~)=−k=1∑∣y∣p~klog2p~k
结论
决策树学习的基本思路是生成一颗泛化能力强的决策树,通过“分而治之”策略,递归地选择最优划分属性,直至满足停止条件。划分选择是决策树学习的关键,常用的准则包括信息熵、信息增益、增益率和基尼指数。这些准则在选择划分属性时,都考虑了样本集合的纯度,以提高模型的划分效果。
在实际应用中,对于连续值特征,决策树采用中点作为划分点,计算信息增益。对于缺失值的处理,通过赋予样本权重,引入缺失值占比,使得信息增益的计算更具鲁棒性。
预剪枝和后剪枝是处理过拟合的两种主要策略。预剪枝在构建决策树的过程中提前停止节点的分裂,可以有效降低过拟合风险,但可能导致信息丢失。后剪枝先构建完整决策树再自下而上进行剪枝,相比预剪枝更加灵活,但训练时间开销较大。
综上所述,决策树通过简洁直观的建模方式,以及对不同问题的适应性,成为一种在实际决策制定中广泛应用的方法。在具体应用中,根据数据特点和问题需求选择适当的划分准则和剪枝策略,有助于构建出高效泛化的决策树模型。
实验分析
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.impute import SimpleImputer
from sklearn.tree import DecisionTreeClassifier
from sklearn.compose import ColumnTransformer
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import OneHotEncoder
from sklearn.metrics import confusion_matrix, classification_report# 读入数据集
data = pd.read_csv('data/Customer-Churn.csv')
data
进行数据的预处理
# 划分特征和标签
X = data.drop("Churn", axis=1)
y = data["Churn"]# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.05, random_state=42)# 定义分类特征和数值特征的列名
categorical_features = X.select_dtypes(include=["object"]).columns
numeric_features = X.select_dtypes(include=["number"]).columns# 创建缺失值填充器
categorical_imputer = SimpleImputer(strategy="most_frequent")
numeric_imputer = SimpleImputer(strategy="mean")# 创建分类特征处理器
categorical_processor = Pipeline(steps=[('imputer', SimpleImputer(strategy='most_frequent')), # 填充缺失值('onehot', OneHotEncoder(handle_unknown='ignore')) # 独热编码
])# 创建预处理步骤
preprocessor = ColumnTransformer(transformers=[("cat", categorical_processor, categorical_features),("num", numeric_imputer, numeric_features)]
)
定义决策树模型,利用网格搜索对象,寻最优超参数。
from sklearn.model_selection import GridSearchCV# 定义决策树模型
dt_classifier = DecisionTreeClassifier(random_state=32)# 定义超参数范围
param_grid = {'classifier__max_depth': [3, 4, 5, 6, 7, None],'classifier__min_samples_split': [2, 3, 4, 5, 6, 10],'classifier__min_samples_leaf': [1, 2, 3, 4],'classifier__ccp_alpha': [0.0, 0.001, 0.002, 0.01] # 增加 ccp_alpha 参数范围
}# 创建包含预处理和决策树的pipeline
pipeline = Pipeline(steps=[('preprocessor', preprocessor),('classifier', dt_classifier)])# 创建网格搜索对象
grid_search = GridSearchCV(pipeline, param_grid, cv=5)# 在训练集上进行网格搜索
grid_search.fit(X_train, y_train)# 输出最佳参数
print("Best Parameters:", grid_search.best_params_)# 获取最佳决策树模型
best_dt_classifier = grid_search.best_estimator_.named_steps['classifier']# 画出决策树
plt.figure(figsize=(20, 10))
plot_tree(best_dt_classifier, feature_names=None, filled=True, class_names=['No', 'Yes'], rounded=True)
plt.show()# 在测试集上评估性能
y_pred = grid_search.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy}')# 计算混淆矩阵
conf_matrix = confusion_matrix(y_test, y_pred)# 打印混淆矩阵
print("Confusion Matrix:")
print(conf_matrix)# 计算其他评估指标
report = classification_report(y_test, y_pred)# 打印其他评估指标
print("\nClassification Report:")
print(report)
Best Parameters: {'classifier__ccp_alpha': 0.001, 'classifier__max_depth': 6, 'classifier__min_samples_leaf': 1, 'classifier__min_samples_split': 2}
Accuracy: 0.8215297450424929
Confusion Matrix:
[[234 30][ 33 56]]Classification Report:precision recall f1-score supportNo 0.88 0.89 0.88 264Yes 0.65 0.63 0.64 89accuracy 0.82 353macro avg 0.76 0.76 0.76 353
weighted avg 0.82 0.82 0.82 353
- 准确度高: 模型的准确度达到了82.15%,表示模型在整体上的预测表现较好。
- 混淆矩阵:
- 对于类别"No",模型有234个真正例,30个假正例,33个假负例,和56个真负例。在类别"No"上表现较好。
- 对于类别"Yes",模型有56个真正例,33个假正例,30个假负例,和234个真负例。在类别"Yes"上的表现相对较弱,召回率较低。
- 分类报告: 提供了更详细的性能指标。
- 在类别"No"上,精确度、召回率和F1分数均较高,说明模型在预测类别"No"时表现良好。
- 在类别"Yes"上,精确度较高,但召回率较低,F1分数也相对较低,说明在预测类别"Yes"时存在一些困难。
- 总体评价: 模型在类别"Yes"上的性能相对较差。
所得到的决策树如下图所示
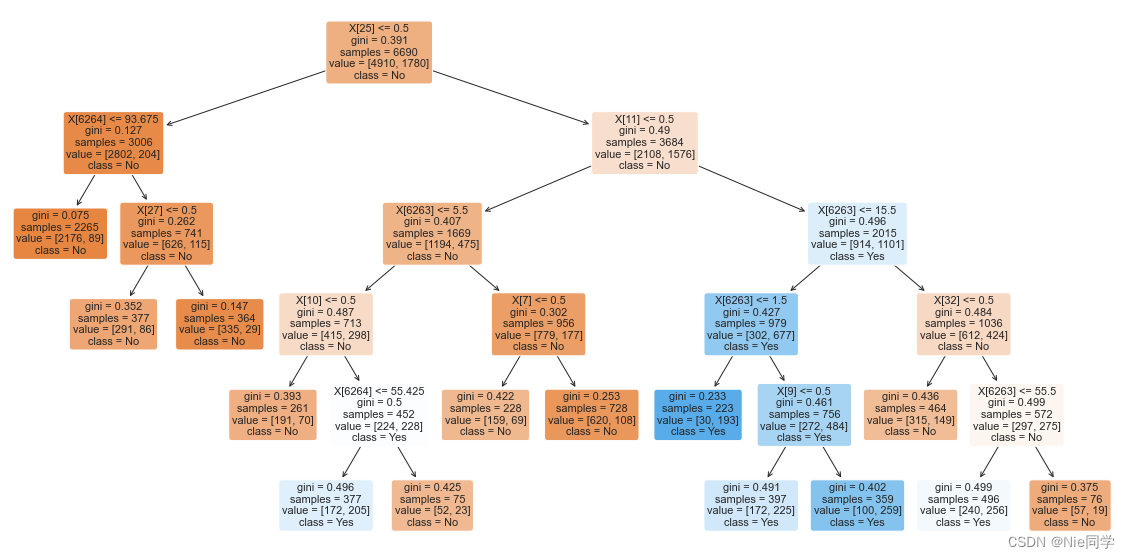

)



)

设置页眉和页码的使用指南——附案例操作)









)

