目录
一. 矩阵Gram-Schmidt正交化的好处
二. 矩阵标准正交化过程
三. 例题
3.1 标准正交化
3.2 算法小结
3.3 优化分析
四. 小结
矩阵有两类等价关系
矩阵对角化
特殊矩阵
一. 矩阵Gram-Schmidt正交化的好处
假如有三个线性独立的向量a,b,c,他们是标准正交的(orthonormal),也就是长度均为1且两两相互正交。
如果任意给一个向量v,计算v投影到a上的向量为:
其中计算结果为标量,代表向量v投影到单位向量a上的长度
向量a和b可以形成一个平面,向量v投影到该平面的向量可以直接计算为:
同理,如果想要计算投影到空间a,b,c上时,则计算为:
可以发现在标准正交向量上的投影计算非常简单,只有简单的内积过程,也就是:
那么如何把任意的矩阵转化为标准正交的矩阵呢?
二. 矩阵标准正交化过程
已知给出三个线性独立向量a,b,c。接下来我们将介绍如何将其转为标准正交向量q1,q2,q3.
先固定向量a的方向,使其与q1一样,接着将其长度变为1,如下:
由此q1即为单位向量。
将向量b分成两部分。一个是和q1同方向的向量,一个是和q2垂直方向的向量。我们只需要去掉和q1同方向的向量即可,如下:
![]()
很明显向量B和q1是互相垂直的,接着把长度转化为1,即为向量q2.来看一个直观的图:
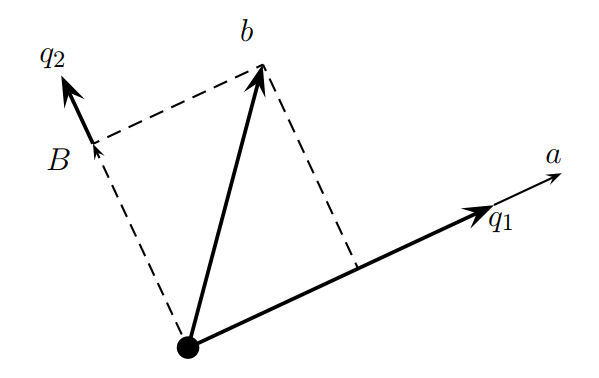
确定好q1和q2后,接下来便可以使用同样的手段处理向量c了。因为a,b,c线性独立,所以向量c不一定在q1和q2形成的平面上。我们就可以把向量c分成两个三个分量:垂直q1和q2平面的分量,和q1同方向的分量,和q2同方向的分量。由此便可以一个新的垂直分量如下:

以上即为整个标准的Gram-Schmidt正交化过程,每次迭代均减去已确定方向的分量,形式化的表达如下:
subtract from every new vector its components in the directions that are already settled
在以上例子中,如果出现第四个向量d,则减去和q1,q2,q3同方向的分量。
三. 例题
3.1 标准正交化
给定三个向量a,b,c,如下:

将向量a转为单位向量即可形成q1,如下:
将第二个向量沿着q1方向的分量减去,即可得到B,如下:

将向量B进行标准化,也就是除以其长度,可得单位向量,如下:
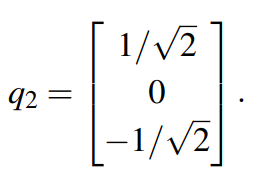
去掉向量c沿着q1和q2的方向向量,可得:

观察发现向量C已经是单位向量,所以q3=C.
将以上标准正交向量q1,q2,q3作为列向量,即可构成正交矩阵Q,如下:

3.2 算法小结
Gram-Schmidt算法的输入是线性独立向量,算法的输出为标准正交的向量
。算法的本质就是迭代过程,当迭代到第j步时,就是用向量
减去沿着
的方向向量,标准公式如下:
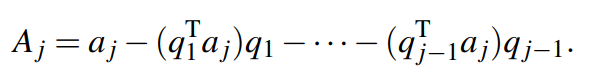
接着单位向量即可计算为:
3.3 优化分析
通过以上例题,我们发现Gram-Schmidt算法经常需要开平方,这给实际运算带来很多不便。比如刚才那个例题中,如果只是保留a,B,C的话,这些向量是垂直的,只是长度不一定为1,这样的话计算起来会方便很多。或者,只是到最后一步才进行开方运算。
将向量b投影到向量a上的分向量为:
由此可计算为:

同样的方法可计算C为:
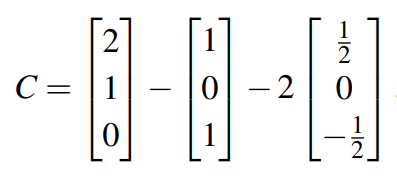
四. 小结
法国哲学家、数学家勒内⦁笛卡尔(Rene Descartes)于1637年创立了笛卡尔坐标系,实现了几何问题代数化,为微积分的建立奠定了基础。和
笛卡尔坐标向量的代数运算可进一步拓展到
欧氏空间,进而拓展到抽象的向量空间的代数运算,这些极大地扩展了数学研究范围。
矩阵有两类等价关系
矩阵相似:
设,若存在非奇异矩阵
,使得:
则称A与B相似。
矩阵合同:
设都是对称矩阵,若存在非奇异矩阵
,使得:
则称A与B合同。
相关性质:
- 若A与B相似,则A与B有相同的特征值;
- 若A与B合同,则A与B有相同的惯性。
矩阵对角化
若存在非奇异矩阵,使得:
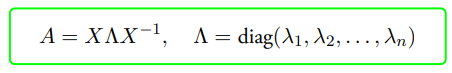
则称A是可对角化的。若A可对角化,则称上式子为A的特征值分解或谱分解。矩阵A对角化的性质:
- A可对角化的充要条件是A具有n个线性无关的特征向量;
- A可对角化的充要条件是A的每个特征值的代数重数和几何重数相等;
- 若A的特征值互不相同,则A可对角化
若方阵A是对称矩阵,则A可对角化。
特殊矩阵
特殊矩阵包括:
单位矩阵,数量矩阵(对角线上元素都是同一个数值),对角矩阵,三对角矩阵(对角线、邻近对角线的上下次对角线上有元素,其他位置均为0的矩阵),上 (下) 三角矩阵,上 Hessenberg 矩阵(当行大于列+1时元素为0),下Hessenberg 矩阵(当列大于行+1时元素为0),带状矩阵(当所有非零元素都集中在以主对角线为中心的带状区域时)
置换 (排列) 矩阵,对称矩阵 (Hermitian 矩阵),反向单位矩阵,反向对称矩阵,斜对称矩阵
Vandermonde 矩阵,Toeplitz 矩阵,循环矩阵,Hankel 矩阵
正定矩阵,半正定矩阵,对角占优矩阵,不可约矩阵
正交矩阵 (酉矩阵),对合矩阵,幂等矩阵 (也称投影矩阵),幂零矩阵
分块矩阵 (块对角, 块三角, ...)

设置页眉和页码的使用指南——附案例操作)









)



)



