力扣日记：【二叉树篇】450. 删除二叉搜索树中的节点

日期：2024.1.11
参考：代码随想录、力扣

450. 删除二叉搜索树中的节点

题目描述

难度：中等

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

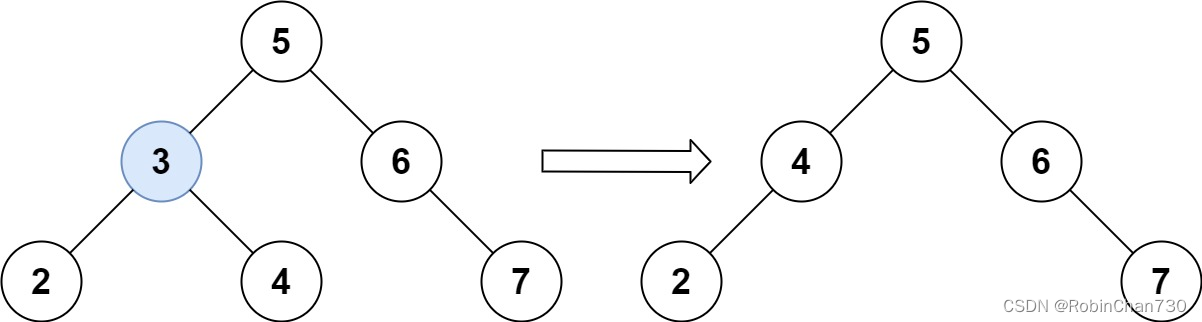
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如上图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 10^4].
• -10^5 <= Node.val <= 10^5
• 节点值唯一
• root 是合法的二叉搜索树
• -10^5 <= key <= 10^5

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

题解

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
#define SOLUTION 1
public:
#if SOLUTION == 1TreeNode* deleteNode(TreeNode* root, int key) {// 空树直接返回(或者找到底也没找到key)if (root == nullptr) return root;// 找到了，开始删除if (root->val == key) {// 如果左节点为空，直接返回右节点if (root->left == nullptr)  return root->right; // 右节点可能为空可能不为空// 如果右节点为空，直接返回左节点else if (root->right == nullptr)    return root->left;  // 左节点不为空// 这里则是左右节点都不为空else {// 如果root的左节点没有右子节点，可以把右子树直接作为左节点的右子树if (root->left->right == nullptr) {root->left->right = root->right;return root->left;  // 返回root的左节点作为新的根节点} // 如果root左节点存在右子节点，则看root的右节点的左子节点else if (root->right->left == nullptr) {root->right->left = root->left;return root->right; // 返回root的右节点作为新的根节点}else {// 这里则是root的左节点有右子节点，且右节点有左子节点// 把root右子树接到root左子树中// 循环找到root的左节点的右子节点为空(最右节点的值是最大的)TreeNode* cur = root->left;while (cur->right != nullptr) {cur = cur->right;}// 此时cur->right为空cur->right = root->right;return root->left; // 把root的左节点返回}}}// 没找到，看大小，继续递归if (key > root->val) {  // 往右找root->right = deleteNode(root->right, key); // 找到会返回新的右子树根节点} else {  // 另一种情况就是往左找root->left = deleteNode(root->left, key);   // }return root;}
#endif
};

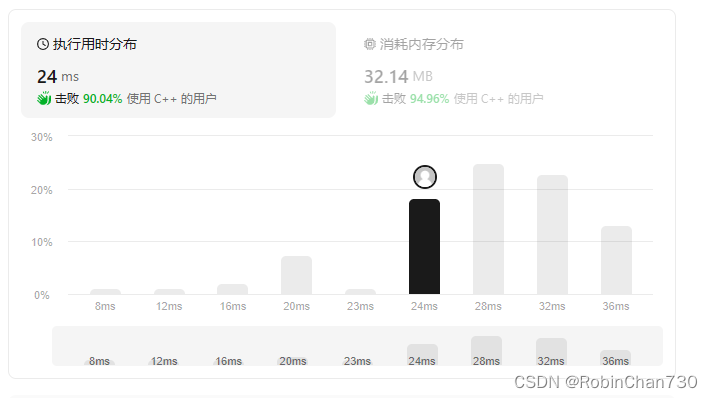
复杂度

时间复杂度：
空间复杂度：

思路总结

• 能解出题来好开心（/(ㄒoㄒ)/~~，虽然过程和代码写的很不简洁，但太难得了（悲
• 注释的过程即为解题思路过程，可以多画点图模拟一下
• 关于找到key后删除当前root节点的思路，分几种情况：
  • 1. 如果root左节点为空，直接返回右节点
  • 2. 如果root右节点为空，直接返回左节点
  • 3. 如果左右节点都不为空
    • 1）首先：考虑 如果root的左节点没有右子节点，可以把右子树直接作为左节点的右子树
    • 2）如果root左节点存在右子节点，则看root的右节点的左子节点，思路同理
    • 3）如果都不满足，即root的左节点有右子节点，且右节点有左子节点
      • 则考虑把root右子树接到root左子树中
      • 通过 不断迭代 root的左子树中的右子节点，直到找到 右子节点为空(因为最最右的右子节点的值是左子树中最大的)
      • 找到后，把root的右子节点接到该空节点处，并返回root的左节点
• 关于删除后返回节点或者递归接收节点的思路：与插入是类似的，都是假定递归函数返回操作（如这里的删除以及上一题的插入）后的新子树根节点，作为当前root节点的新子节点。
• 如果还未找到key，则可根据二叉搜索树的性质，根据key的大小往左或往右递归寻找，直到递归到空节点则直接返回nullptr。
• 改进：实际上，对于删除节点时root左右节点都不为空的情况（即第3点），可以都作为第三种情况来考虑（即第3）点），即直接考虑将root右子树接到root左子树中（左子树的右子节点为空则直接接到该空节点处即可，否则就进行迭代找到空右子节点）