MATLAB全局最优搜索函数：GlobalSearch函数

摘要：本文介绍了 GlobalSearch 函数的使用句式（一）、三个运行案例（二）、 GlobalSearch 函数的参数设置（三）、GlobalSearch 注意事项及必要说明（五）等内容。详细介绍如下：

一、函数句法

Syntax
gs = GlobalSearch
gs = GlobalSearch(Name,Value)
gs = GlobalSearch(oldGS,Name,Value)
gs = GlobalSearch(ms)

二、实战案例

（1）Example1：Run GlobalSearch on Multidimensional Problem

gs = GlobalSearch creates gs, a GlobalSearch solver with its properties set to the defaults.

代码：

rng default % For reproducibility
gs = GlobalSearch;
sixmin = @(x)(4*x(1)^2 - 2.1*x(1)^4 + x(1)^6/3 ...+ x(1)*x(2) - 4*x(2)^2 + 4*x(2)^4);
problem = createOptimProblem('fmincon','x0',[-1,2],...'objective',sixmin,'lb',[-3,-3],'ub',[3,3]);
[x,fval] = run(gs,problem)

运行结果：

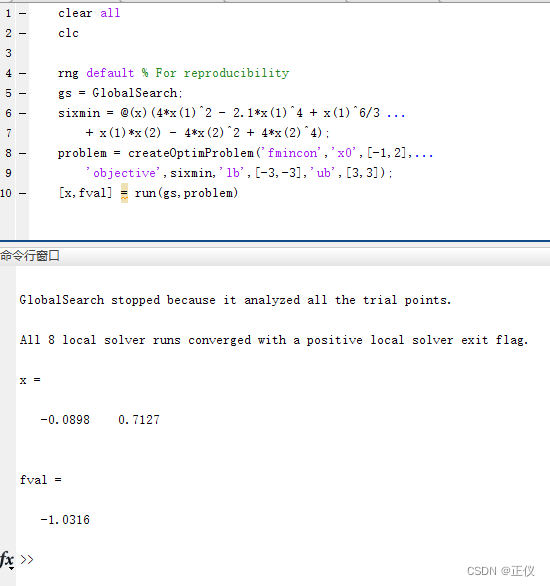
注意： 在MATLAB中，rng default 的作用是将随机数生成器的种子（seed）设置为默认值。种子是一个起始值，用于生成伪随机数序列。通过将种子设置为默认值，你可以确保在每次运行程序时，生成的伪随机数序列都是相同的，从而实现结果的可复现性。具体而言，rng default将随机数生成器的种子设置为 MATLAB 的默认值，这样每次运行代码时，生成的随机数序列都将相同。这对于需要随机性的算法，但又需要可重复的结果的情况非常有用，例如在进行随机实验或优化算法中。

（2）Example2：Run GlobalSearch on 1-D Problem

Consider a function with several local minima.

fun = @(x) x.^2 + 4*sin(5*x);
fplot(fun,[-5,5])

图示如下：

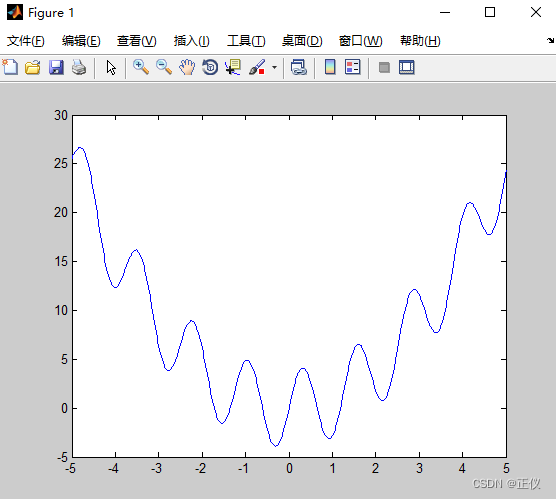
To search for the global minimum, run GlobalSearch using the fmincon ‘sqp’ algorithm.

代码：

rng default % For reproducibility
opts = optimoptions(@fmincon,'Algorithm','sqp');
problem = createOptimProblem('fmincon','objective',...fun,'x0',3,'lb',-5,'ub',5,'options',opts);
gs = GlobalSearch;
[x,f] = run(gs,problem)

运行结果：

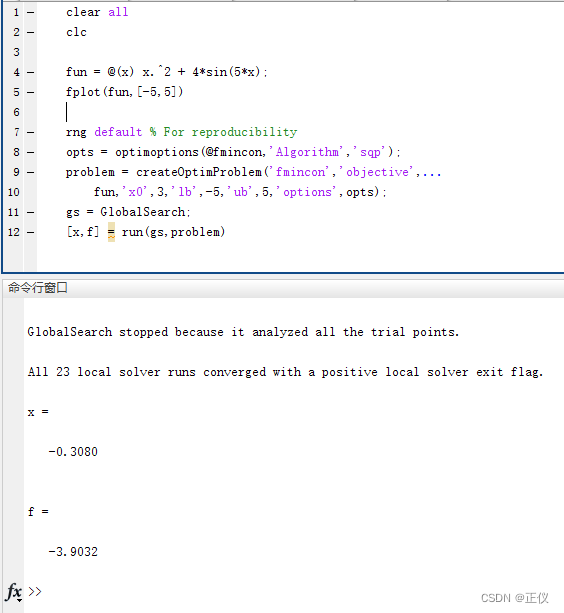
（3）Example3：调用fmincon时，含非线性约束的 GlobalSearch 函数用法

主函数代码如下：

clear all
clc% 目标函数
fun = @(x) sin(x(1)) + 0.1 * x(2)^2;% 非线性约束
nonlcon = @(x) constraintFunction(x);% 定义优化问题
problem = createOptimProblem('fmincon', 'objective', fun, 'nonlcon', nonlcon, 'x0', [0, 0], 'lb', [-5, -5], 'ub', [5, 5]);% 创建 GlobalSearch 对象
gs = GlobalSearch;% 运行全局搜索
[x, fval, exitflag, output] = run(gs, problem);% 显示结果，包括函数计算次数
disp('全局最优解：');
disp(['x = ' num2str(x)]);
disp(['目标函数值 = ' num2str(fval)]);
disp(['退出标志 = ' num2str(exitflag)]);
disp(['函数计算次数：' num2str(output.funcCount)]);

子函数代码如下：

% 定义约束函数
function [c, ceq] = constraintFunction(x)c = x(1)^2 + x(2)^2 - 1;  % 非线性不等式约束ceq = [];  % 非线性等式约束为空
end

运行结果：

需要注意，nonlcon 的非线性约束的写法！
另外，如果需要向非线性约束中传递参数，直接加参数即可，主函数中改为：

% 非线性约束
a=1;
nonlcon = @(x) constraintFunction(x,a);

子函数中改为下式即可：

% 定义约束函数
function [c, ceq] = constraintFunction(x,a)c = a*x(1)^2 + x(2)^2 - 1;  % 非线性不等式约束ceq = [];  % 非线性等式约束为空
end

三、GlobalSearch 函数的参数设置

（1）基于 MultiStart 设置 GlobalSearch 参数

Create a nondefault MultiStart object.

ms = MultiStart('FunctionTolerance',2e-4,'UseParallel',true)

Create a GlobalSearch object that uses the available properties from ms.

gs = GlobalSearch(ms)

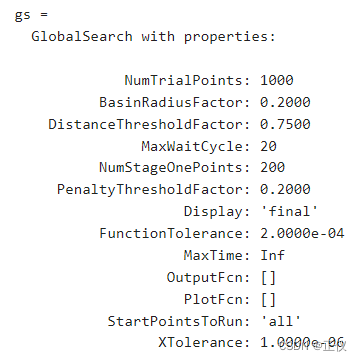
gs has the same nondefault value of FunctionTolerance as ms. But gs does not use the UseParallel property.

（2）直接设置 GlobalSearch 参数

Create a GlobalSearch object with a FunctionTolerance of 1e-4.

gs = GlobalSearch('FunctionTolerance',1e-4)

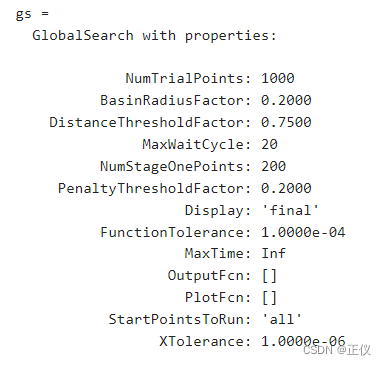
Update the XTolerance property to 1e-3 and the StartPointsToRun property to ‘bounds’.

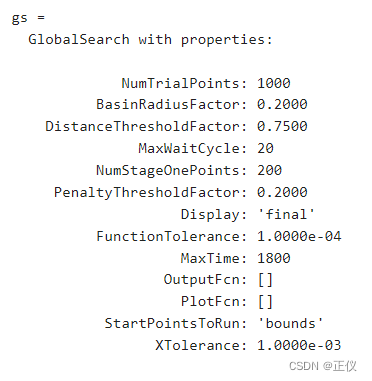
gs = GlobalSearch(gs,'XTolerance',1e-3,'StartPointsToRun','bounds')

You can also update properties one at a time by using dot notation.

gs.MaxTime = 1800

（3）设置 GlobalSearch 参数的必要性（实战案例）

当你觉得求解的性能不太好时，一定要增加初始点的数量！我记录一下自己运行的案例，同样的代码，GlobalSearch 默认是1000个初始点，运行结果如下：

有的基站的覆盖半径依旧很大，且没必要那么大，由此可知解显然非最优。因此，我提高了初始点的数量为 10000 个！扩大了10倍：

gs = GlobalSearch('NumTrialPoints', 10000);

覆盖性能明显好转：

因此，在使用 GlobalSearch 函数求解非凸优化问题最优解时，别忘了要设置足够大的初始点！这样才可以提高找到最优解的概率。

四、Algorithms 原理

For a detailed description of the algorithm, see GlobalSearch Algorithm. Ugray et al. [1] describe both the algorithm and the scatter-search method of generating trial points.

参考文献：[1] Ugray, Zsolt, Leon Lasdon, John Plummer, Fred Glover, James Kelly, and Rafael Martí. Scatter Search and Local NLP Solvers: A Multistart Framework for Global Optimization. INFORMS Journal on Computing, Vol. 19, No. 3, 2007, pp. 328–340.

五、GlobalSearch 注意事项及必要说明

（1）GlobalSearch 与 fmincon 的区别

问：GlobalSearch函数中可以调用fmincon函数。因此，一个很自然的问题是：在GlobalSearch函数中调用fmincon 与直接用fmincon函数求解，两者的运行结果会有什么区别？
答：（1）全局搜索 vs 局部搜索：fmincon 是一个局部优化算法，它试图找到一个局部最小值，而不保证找到全局最小值。
GlobalSearch 利用多个局部优化起点和策略，通过在搜索空间中的多个位置进行局部搜索，尝试找到全局最小值；（2）多起点搜索：fmincon 需要提供一个初始点，并在该点周围进行局部搜索。GlobalSearch 则在搜索空间中的多个随机或预定义的起始点上运行局部搜索，以覆盖可能的全局最小值；（3）计算资源：由于 GlobalSearch 在多个点上并行运行局部搜索，可能需要更多的计算资源。fmincon 在单个起始点上运行，因此计算资源需求可能较低。

（2）GlobalSearch 运行结果含义及说明

使用 GlobalSearch 得到如下运行结果，表示什么含义？

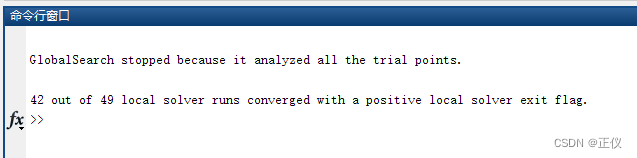
“GlobalSearch stopped because it analyzed all the trial points.”解读： 意思是 GlobalSearch 停止了，因为它已经分析了所有试点（trial points）。在全局优化问题中，GlobalSearch 通常会在不同的初始点附近运行局部优化器，试图找到全局最优解。这个消息表明它已经尝试过所有计划的试点，无法再继续分析其他试点，因此停止；
“42 out of 49 local solver runs converged with a positive local solver exit flag.”解读： 意思是在总共的 49 次局部优化器（local solver）运行中，有 42 次成功地收敛到一个局部最优解，并且这些局部优化器的退出标志（exit flag）是正的。在 GlobalSearch 的执行过程中，针对不同的初始点，会运行局部优化器来寻找局部最优解。这个消息表明其中大多数的局部优化运行都是成功的，并且它们在找到局部最优解后成功地退出了。
总之，该结果表示所得的最优解相对可信、可靠。

（3）GlobalSearch 函数调用 fmincon 时，如何设置 fmincon 的options？

代码实际设置案例：

% 目标函数
fun     = @( Upper_Decision ) GS_myfit  ( Upper_Decision, parameter, User );% 非线性约束
nonlcon = @( Upper_Decision ) GS_nonlcon( Upper_Decision, parameter, User ) ;% 定义优化问题
problem = createOptimProblem('fmincon', 'objective', fun, 'nonlcon', nonlcon, 'x0', x0 , 'lb', LB, 'ub', UB,  'options', optimoptions('fmincon', 'ScaleProblem', 'obj-and-constr'));% 创建 GlobalSearch 对象
gs = GlobalSearch;% 运行全局搜索
[x, fval, exitflag, output] = run( gs, problem );