一、检查是否配置有ohpm环境
1、新打开一个终端输入export,查看是否有 ohpm路径:
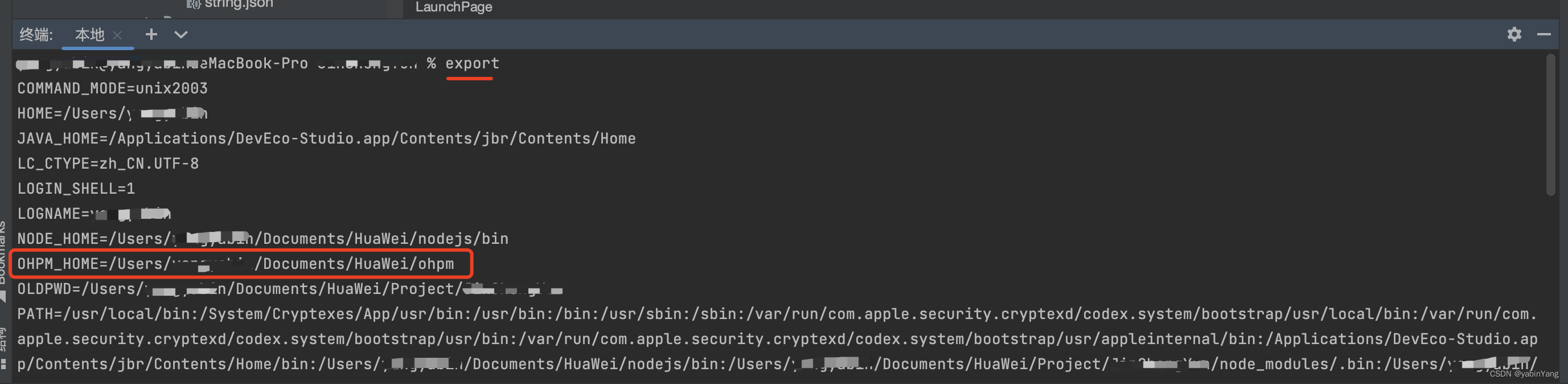 二、如果没有找到ohpm路径,开始配置环境 。
二、如果没有找到ohpm路径,开始配置环境 。
1、查找本机ohpm路径,并记录ohpm解释器的路径:
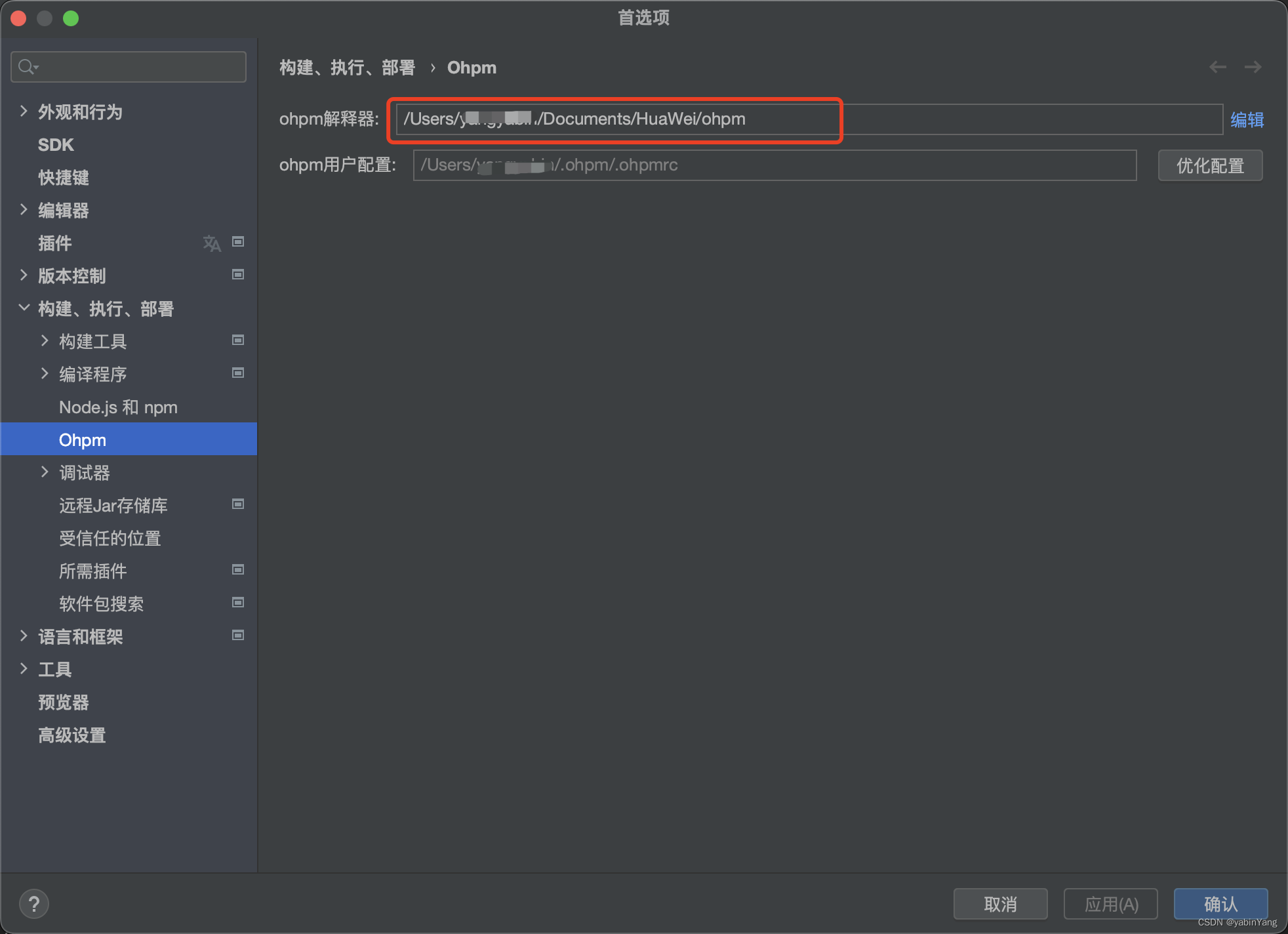
2、打开终端工具,执行命令 echo $SHELL 。
a、输入结果为/bin/base,则执行 vi ~/.bash_profile;
b、输入结果为/bin/zsh,则执行vi ~/.zshrc;
3、单击字母“i”,进入Insert模式。
4、将记录的路径写进:
export OHPM_HOME=/Users/xxx/Documents/HuaWei/ohpm
export PATH=${PATH}:${OHPM_HOME}/bin5、编辑完成后,单击ESC键,退出编辑模式,然后输入“:wq”,单击Enter键保存。
6、执行以下命令,使配置的环境变量生效:
a、如果打开的是.bash_prifile文件,则输入 source ~/.bash_profile;
b、如果打开的是.zshrc文件,则输入 source ~/.zshrc;
6、环境变量配置完成,完全关闭并重启DevEco Studio。
![[力扣 Hot100]Day3 最长连续序列](http://pic.xiahunao.cn/[力扣 Hot100]Day3 最长连续序列)




笔记5)









![CVE-2023-49070:Apache Ofbiz XML-RPC远程命令执行漏洞复现[附POC]](http://pic.xiahunao.cn/CVE-2023-49070:Apache Ofbiz XML-RPC远程命令执行漏洞复现[附POC])


![【算法每日一练]-动态规划 (保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔](http://pic.xiahunao.cn/【算法每日一练]-动态规划 (保姆级教程 篇16) #纸带 #围栏木桩 #四柱河内塔)
