一、题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

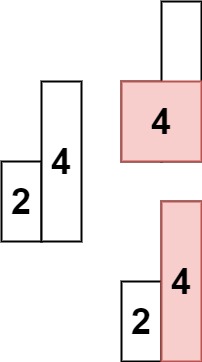
输入： heights = [2,4]
输出： 4

提示：

• 1 <= heights.length <=105
• 0 <= heights[i] <= 104

二、思路分析

使用栈空间来解决本题，通过空间换时间的方式。

三、代码参考

1、Java

class Solution {public int largestRectangleArea(int[] heights) {// 获取数组长度int len = heights.length;// 数组长度为 0 或者 1 时直接返回if(len == 0){return 0;}if(len == 1){return heights[0];}// 用来返回最大面积，初始值为 0int area = 0;// 创建栈空间做辅助Deque<Integer> stack = new ArrayDeque<>();// 循环遍历数组for(int i = 0; i < len; i++){// while(!stack.isEmpty() && heights[stack.peekLast()] > heights[i]){// 获取栈顶高度，并移除当前栈顶int height = heights[stack.removeLast()];// 做特殊的处理，如果当前栈顶的高度和上一个栈顶的高度相同，则也需要进行弹栈while(!stack.isEmpty() && heights[stack.peekLast()] == height){// 移除栈顶元素stack.removeLast();}// 创建宽度变量，初始值为 0int width = 0;// 如果栈为空，说明，有效柱体能够从 i 的左边一直延伸到第一个开始if(stack.isEmpty()){// 所以此时的宽度为 iwidth = i;}else {width = i - stack.peekLast() - 1;}// 计算面积, 长 * 宽，并获取最大面积area = Math.max(area, height * width);}// 将下标存入栈空间中stack.addLast(i);}// 将当前栈中的所有元素弹出while(!stack.isEmpty()){// 获取栈顶高度，并移除当前栈顶int height = heights[stack.removeLast()];// 做特殊的处理，如果当前栈顶的高度和上一个栈顶的高度相同，则也需要进行弹栈while(!stack.isEmpty() && heights[stack.peekLast()] == height){// 移除栈顶元素stack.removeLast();}// 创建宽度变量，初始值为 0int width = 0;// 如果栈为空，说明，有效柱体能够从 i 的左边一直延伸到第一个开始if(stack.isEmpty()){// 所以此时的宽度为 lenwidth = len;}else {width = len - stack.peekLast() - 1;}// 计算面积, 长 * 宽，并获取最大面积area = Math.max(area, height * width);}// 返回面积结果return area;}
}

2、Python

class Solution:def largestRectangleArea(self, heights: List[int]) -> int:size = len(heights)area = 0stack = []for i in range(size):while len(stack) > 0 and heights[i] < heights[stack[-1]]:height = heights[stack.pop()]while len(stack) > 0 and height == heights[stack[-1]]:stack.pop()if len(stack) > 0:width = i - stack[-1] - 1else:width = iarea = max(area, height * width)stack.append(i)while len(stack) > 0 is not None:height = heights[stack.pop()]while len(stack) > 0 and height == heights[stack[-1]]:stack.pop()if len(stack) > 0:width = size - stack[-1] - 1else:width = sizearea = max(area, height * width)return area