一、算法介绍

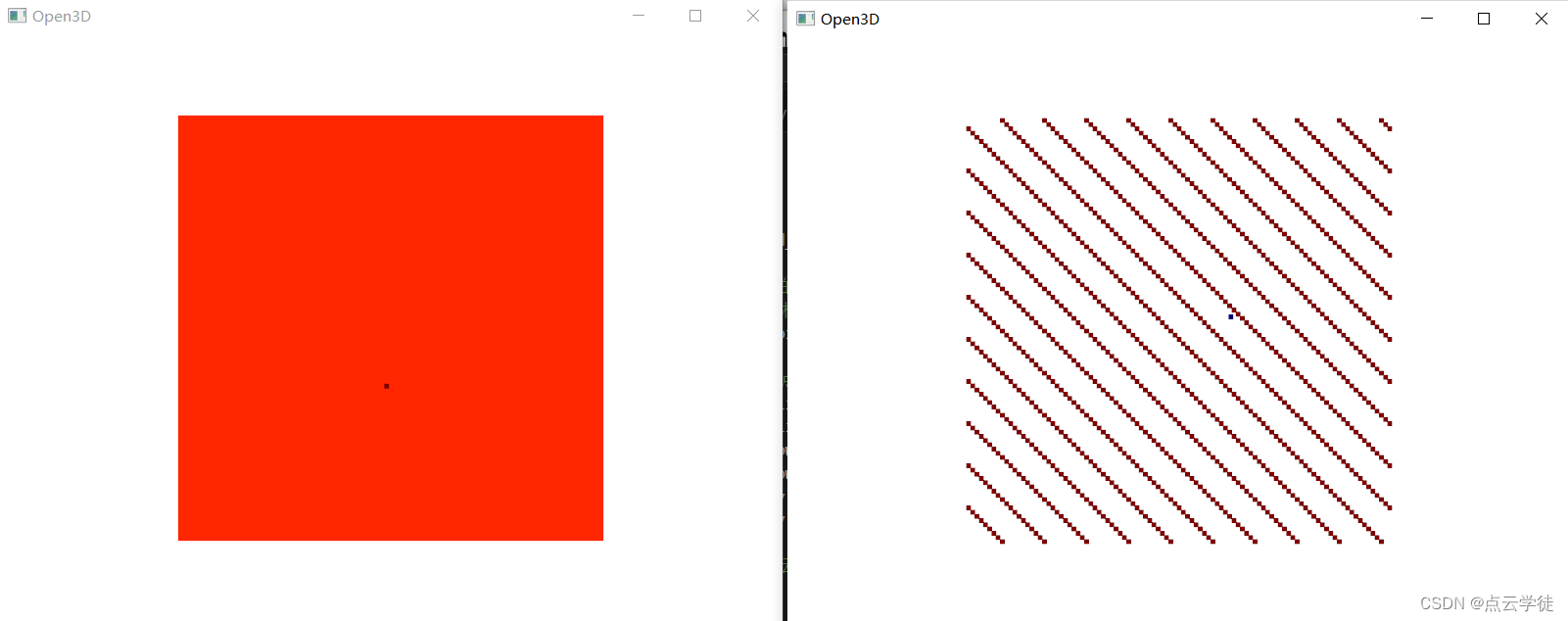
点云抽稀在计算机图形学和计算机视觉中有着广泛的应用，其作用包括但不限于以下几点：

数据压缩： 点云抽稀可以有效地减少点云数据量，从而节省存储空间和降低数据传输成本。

加速处理： 较为密集的点云通常需要更多的计算资源进行处理，抽稀可以减少数据点的数量，从而加快处理速度和提高计算效率。

去除噪声： 一些点云数据可能受到噪声的影响，通过抽稀可以去除一些无意义的离散噪声点，使得数据更加干净。

可视化优化： 在进行点云可视化时，过于密集的点云可能会导致可视化效果混乱，抽稀可以使可视化结果更清晰易懂。

简化模型： 对于点云表示的三维模型，抽稀可以简化模型并减少细节，使得模型更易处理和渲染。

总的来说，点云抽稀可以通过减少数据量、加快处理速度、去除噪声等方式，对点云数据进行预处理和优化，以满足不同应用场景下的需求。

二、算法实现

1.代码

代码如下（示例）：

import open3d as o3d# 读取点云数据
point_cloud = o3d.io.read_point_cloud("D:\\shuju\\原始点云.pcd")# 设置均匀采样（半径滤波）的参数
# 这里以每10个点进行一次采样为例
filtered_point_cloud = point_cloud.uniform_down_sample(every_k_points=10)# 创建可视化窗口并添加原始点云和滤波后的点云
vis_original = o3d.visualization.Visualizer()
vis_filtered = o3d.visualization.Visualizer()
vis_original.create_window(width=800, height=600)
vis_filtered.create_window(width=800, height=600)
vis_original.add_geometry(point_cloud)
vis_filtered.add_geometry(filtered_point_cloud)# 显示原始点云和滤波后的点云
vis_original.run()
vis_filtered.run()# 写出滤波后的点云数据
o3d.io.write_point_cloud("D:\\shuju\\结果点云.pcd", filtered_point_cloud)