前言

我们先来笼统的介绍一下今天的三个内容。

适配器——简单的理解就是复用，用已经实现的轮子，来继续实现某种功能。
反向迭代器——原理很简单，就是对称+复用（已经造好的正向迭代器）
仿函数——与函数用法相同的类，用于排序，比如大堆，小堆，升序，降序。

一、适配器

适配器的功能，在我们模拟实现栈和对列时十分方便！
先用这两个例子感受一下。

①模拟实现栈

	template<class T,class Con = deque<T>>class stack{public:void push(const T& val){st.push_back(val);}void pop(){st.pop_back();}T& top(){return st[st.size() - 1];}size_t size(){return st.size();}bool empty(){return st.empty();}private:Con st;};

②模拟实现对列

	template<class T, class Con = deque<T>>class queue{public:void push(const T& val){qu.push_back(val);}void pop(){qu.pop_front();}T& front(){return qu[0];}size_t size(){return qu.size();}bool empty(){return qu.empty();}private:Con qu;};

这里的模板参数：

template<class T, class Con = deque<T>>//这就是适配器

看完这两个例子，你可能会明白，并且可能会惊讶于适配器的方便之处。

并且这里也给了模板一个用法——缺省参数。

且如果是全缺省的话，我们示例化还是要给参数列表的。

如下：

stack<> st;

再来谈谈deque，你可能会好奇，这里在栈的第二个缺省参数为啥不给vector<T>, 对列的第二个缺省参数为啥不给list<T>。

要弄清楚原因我们先得了解deque的基本结构：

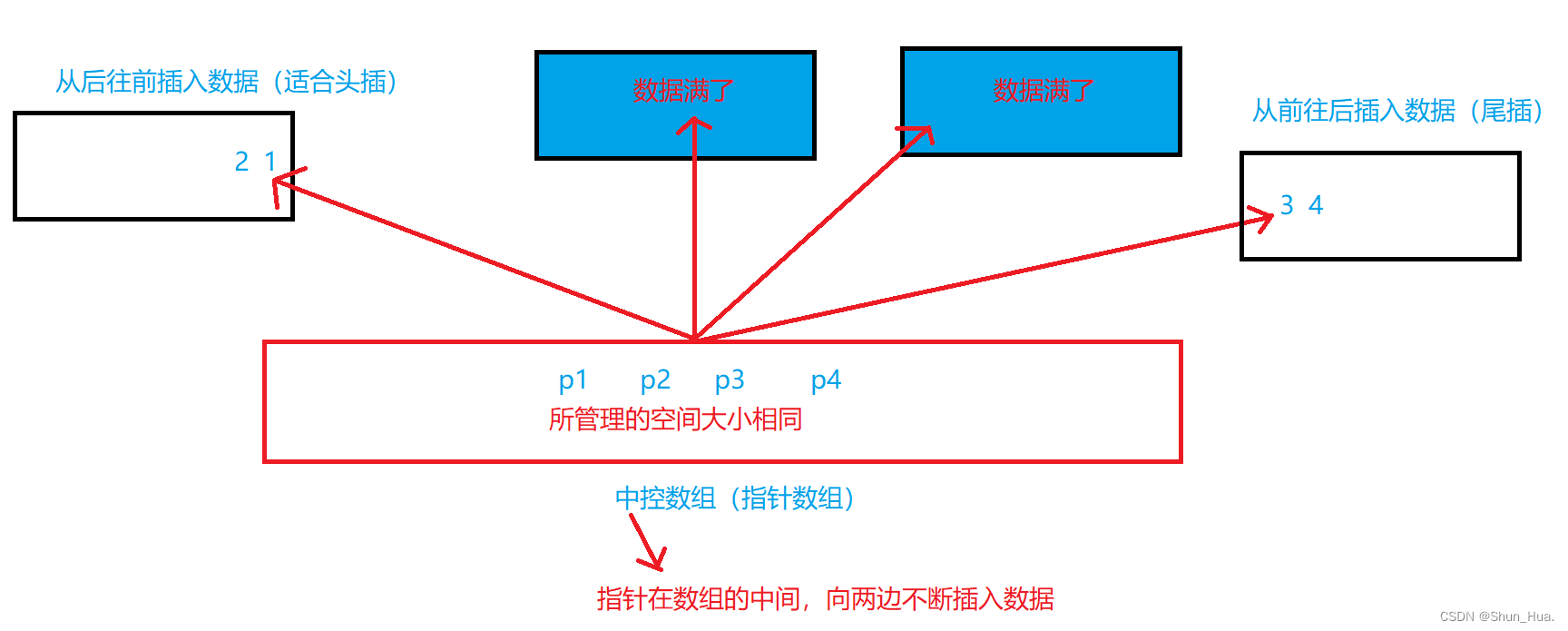
在这里插入图片描述

我们知道这个中控数组一旦满了，就要考虑扩容的问题，那该如何扩呢？

只需要将中控数组进行扩容，然后将指针拷贝过去即可。

因此相较于vector无需动数据即可完成扩容！—— 提高了扩容的效率。

相较于vector，这种结构也支持随机访问，不过得通过计算，这样高频率的随机访问效率会降低，缓冲命中率也有一定的下降。

相较于list，由于list是单个申请单个释放，因此deque的缓冲命中率较高。

但是相较于list，如果deque要在中间插入数据，那效率就会降低，这一点不如list。

这样：

stack结构，实现尾插尾删功能，如果要考虑扩容的效率，deque的优势更大。
queue结构，实现尾插头删功能，如果要考虑到缓冲命中率，deque的优势更大。

因此库里采用了deque来实现栈和对列！

二、反向迭代器

我们先来看库里的实现方式：

vector
list

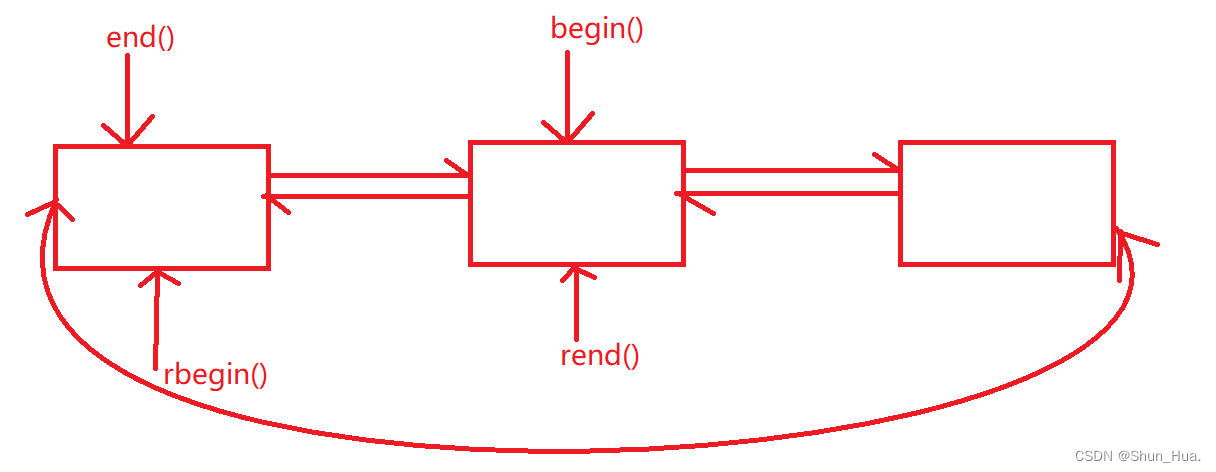
可以看到，这里呈现对称的方式，但是如何解引用是关键。

库里是这样实现的：

Reverse_iterator operator* ()
{Iterator tmp(_it);return *--tmp;
}

这里使用了正向迭代器的拷贝构造，然后再减减访问反向迭代器的下一个元素，这样实现了错位，也能刚好利用实现好的正向迭代器。

剩余的就不难实现了：

	template<class Iterator, class Ref, class Ptr>struct Reverse_iterator{typedef Reverse_iterator<Iterator, Ref, Ptr> self;//自定义的类型不能被当做类名进行使用Reverse_iterator(const Iterator& it){_it = it;}self& operator ++(){_it--;return *this;}self operator ++(int){self tmp(_it);_it--;return self;}Ref operator* (){Iterator tmp(_it);return *--tmp;}Ptr operator->(){return _it.operator->();}bool operator!=(const Reverse_iterator&it)const{return _it != it._it;}bool operator==(const Reverse_iterator& it)const{return _it == it._it;}Iterator _it;};

然后我们只需在容器里加上下面的代码即可完成复用！

		typedef list_iterator<T,T&,T*> iterator;typedef list_iterator<T,const T&,const T*> const_iterator;typedef Reverse_iterator<iterator, T, T*> reverse_iterator;typedef Reverse_iterator <const_iterator, const T, const T*>\const_reverse_iterator;reverse_iterator rbegin(){return end();//这里会调用拷贝构造}reverse_iterator rend(){return begin();}

三、仿函数

我们这里先实现一个优先级对列——大堆。

	template<class T,class Container = vector<T>>class priority_queue{//建大堆void AdjustDown(int parent){//假设左孩子较大size_t child = parent * 2 + 1;//因为是往下比较，所以child应在范围内while (child < con.size()){//先选出来较大的孩子，当然前提得存在。if (child + 1 < con.size() && con[child] < con[child + 1]){child = child + 1;}//再跟父节点进行比较，如果孩子大就换if (con[parent]< con[child]){swap(con[parent], con[child]);//因为是向下比较的，所以要看parent是不是还比下面的孩子大。parent = child;child = parent * 2 + 1;}else{break;}}}//建大堆void AdjustUp(int child){int parent = (child - 1) / 2;while (parent >= 0){if (con[parent] < con[child]){swap(con[parent], con[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}public:template<class InputIterator>priority_queue(InputIterator first, InputIterator last){InputIterator it = first;while (it != last){con.push_back(*it);it++;}//进行调堆//从最后一个叶子结点的父节点开始。//时间复杂度O(N)for (int i = ((con.size() - 1) - 1) / 2; i >= 0; i--){AdjustDown(i);}}void pop(){swap(con[0], con[con.size() - 1]);con.pop_back();AdjustDown(0);}void push(const T& val){con.push_back(val);AdjustUp(con.size() - 1);}size_t size(){return con.size();}bool empty(){return con.empty();}T top()const{return con[0];}priority_queue(){}private:Container con;};

这里的大堆算是实现了，借助这二叉树的一点点知识。

那如果我们还要实现小堆呢？

用不用cv一份，再改呢？其实不用，只需要写一个仿函数即可。

	template<class T>struct Less{bool operator()(const T &x1 ,const T& x2){return x1 < x2;}};template<class T>struct Greater{bool operator()(const T& x1, const T& x2){return x1 > x2;}};

如何使用呢？用类模板+重载函数的掉用。

template<class T,class Container = vector<T>,class Compare = Less<T>>
class priority_queue
{//建大堆void AdjustDown(int parent){//假设左孩子较大size_t child = parent * 2 + 1;//因为是往下比较，所以child应在范围内while (child < con.size()){//先选出来较大的孩子，当然前提得存在。if (child + 1 < con.size() && com(con[child] , con[child + 1])){child = child + 1;}//再跟父节点进行比较，如果孩子大就换if (com(con[parent], con[child])){swap(con[parent], con[child]);//因为是向下比较的，所以要看parent是不是还比下面的孩子大。parent = child;child = parent * 2 + 1;}else{break;}}}//建大堆void AdjustUp(int child){int parent = (child - 1) / 2;while (parent >= 0){if (com(con[parent] , con[child])){std::swap(con[parent], con[child]);child = parent;parent = (child - 1) / 2;}else{break;}}}
public:template<class InputIterator>priority_queue(InputIterator first, InputIterator last){InputIterator it = first;while (it != last){con.push_back(*it);it++;}//进行调堆//从最后一个叶子结点的父节点开始。//时间复杂度O(N)for (int i = ((con.size() - 1) - 1) / 2; i >= 0; i--){AdjustDown(i);}}void pop(){swap(con[0], con[con.size() - 1]);con.pop_back();AdjustDown(0);}void push(const T& val){con.push_back(val);AdjustUp(con.size() - 1);}size_t size(){return con.size();}bool empty(){return con.empty();}T top()const{return con[0];}priority_queue(){}
private:Container con;Compare com;
};