目录
- 引出
- 散列表Hash table
- 关键字Key和散列函数(hash function)
- 散列函数
- 解决collision哈希冲突(碰撞)
- 分离链接法(separate chaining)
- 探测散列表(probing hash table)
- 双散列(double hashing)
- Java标准库中的散列表
- 总结
引出
1.散列表,key,散列函数;
2.哈希冲突的解决;
3.string中的hashCode;
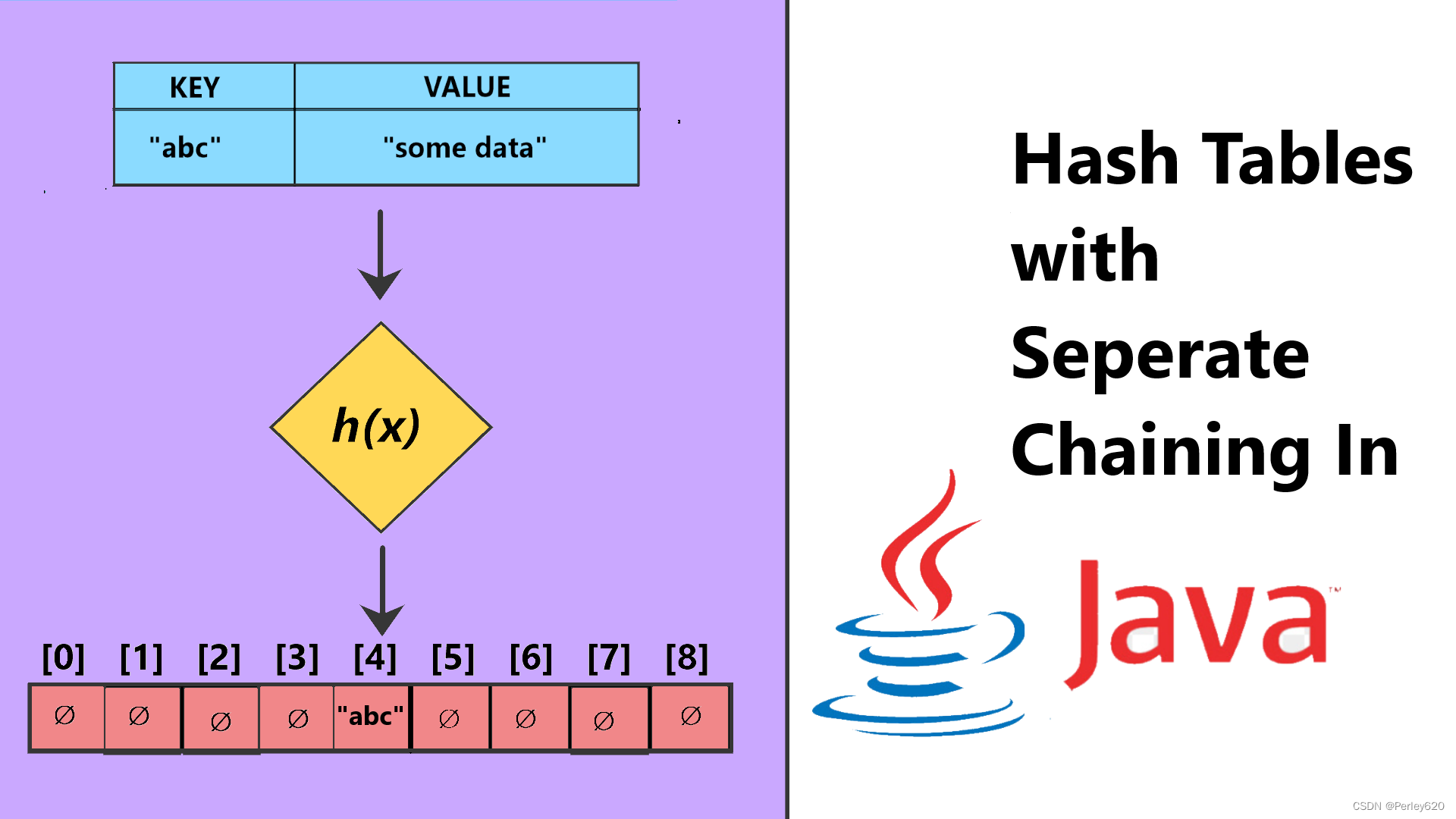
散列表Hash table
查找树ADT,它允许对元素的集合进行各种操作。本章讨论散列表(hash table)ADT,不过它只支持二叉查找树所允许的一部分操作。散列表的实现常常叫作散列(hashing)。散列是一种用于以常数平均时间执行插入、删除和查找的技术。但是,那些需要元素间任何排序信息的树操作将不会得到有效的支持。因此,诸如findMin、findMax以及以线性时间将排过序的整个表进行打印的操作都是散列所不支持的。
- 看到实现散列表的几种方法。
- 解析地比较这些方法。
- 介绍散列的多种应用。
- 将散列表和二叉查找树进行比较。
关键字Key和散列函数(hash function)
理想的散列表数据结构只不过是一个包含一些项(itm)的具有固定大小的数组。通常查找是对项的某个部分(即数据域)进行的。这部分就叫作关键字(key)。
例如,项可以由一个字符串(它可以作为关键字)和其他一些数据域组成(例如,姓名是大型雇员结构的一部分)。我们把表的大小记作TableSize,并将其理解为散列数据结构的一部分,而不仅仅是浮动于全局的某个变量。通常的习惯是让表从0到TableSize-1变化;稍后我们就会明白为什么要这样做。
每个关键字被映射到从0到TableSize-1这个范围中的某个数,并且被放到适当的单元中。这个映射就叫作散列函数(hash function),理想情况下它应该计算起来简单,并且应该保证任何两个不同的关键字映射到不同的单元。不过,这是不可能的,因为单元的数目是有限的,而关键字实际上是用不完的。因此,我们寻找一个散列函数,该函数要在单元之间均匀地分配关键字。
图5-1是完美情况的一个典型。在这个例子中,john散列到3,phil散列到4,dave散列到6,mary散列到7。

这就是散列的基本想法。剩下的问题就是要选择一个函数,决定当两个关键字散列到同一个值的时候(这叫作冲突(collision))应该做什么以及如何确定散列表的大小。
散列函数

这个散列函数利用到事实:允许溢出。这可能会引进负的数,因此在末尾有附加的测试。图5-4所描述的散列函数就表的分布而言未必是最好的,但确实具有极其简单的优点而且速度也很快。如果关键字特别长,那么该散列函数计算起来将会花费过多的时间。在这种情况下通常的经验是不使用所有的字符。此时关键字的长度和性质将影响选择。例如,关键字可能是完整的街道地址,散列函数可以包括街道地址的几个字符,也许还有城市名和邮政编码的几个字符。有些程序设计人员通过只使用奇数位置上的字符来实现他们的散列函数,这里有这么一层想法:用计算散列函数节省下的时间来补偿由此产生的对均匀地分布的函数的轻微干扰。

解决collision哈希冲突(碰撞)
剩下的主要编程细节是解决冲突的消除问题。如果当一个元素被插入时与一个已经插入的元素散列到相同的值,那么就产生一个冲突,这个冲突需要消除。解决这种冲突的方法有几种,我们将讨论其中最简单的两种:分离链接法和开放定址法。
分离链接法(separate chaining)
分离链接法(separate chaining)
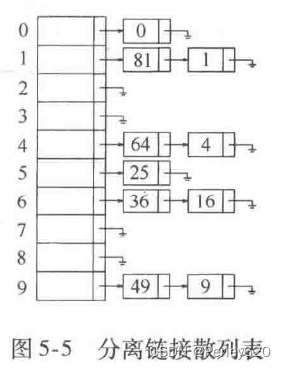
解决冲突的第一种方法通常叫作分离链接法(separate chaining),其做法是将散列到同一个值的所有元素保留到一个表中。我们可以使用标准库表的实现方法。如果空间很紧,则更可取的方法是避免使用它们(因为这些表是双向链接的并且浪费空间)。本节我们假设关键字是前10个完全平方数并设散列函数就是hash(x)=xmod10(表的大小不是素数,用在这里是为了简单)。
探测散列表(probing hash table)
探测散列表(probing hash table)

分离链接散列算法的缺点是使用一些链表。由于给新单元分配地址需要时间(特别是在其他语言中),因此这就导致算法的速度有些减慢,同时算法实际上还要求对第二种数据结构的实现。另有一种不用链表解决冲突的方法是尝试另外一些单元,直到找出空的单元为止。更常见的是,单元h(x),h,(x),h2(x),…相继被试选,其中h:(x)=(hash(x)+f(i)mod
TableSize,且f(0)=0。函数f是冲突解决方法。因为所有的数据都要置入表内,所以这种解决方案所需要的表要比分离链接散列的表大。一般说来,对于不使用分离链接的散列表来说,其装填因子应该低于入=0.5。我们把这样的表叫作探测散列表(probing hash table)。现在我们就来考察三种通常的冲突解决方案。
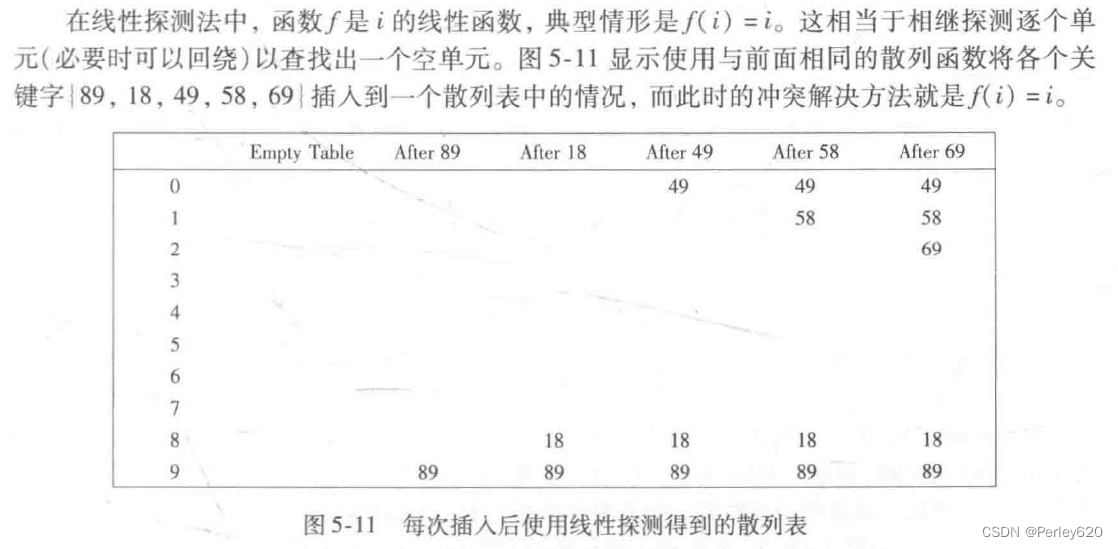
第一个冲突在插人关键字49时产生;它被放入下一个空闲地址,即地址0,该地址是开放的。关键字58先与18冲突,再与89冲突,然后又和49冲突,试选三次之后才找到一个空单元。对69的冲突用类似的方法处理。只要表足够大,总能够找到一个自由单元,但是如此花费的时间是相当多的。更糟的是,即使表相对较空,这样占据的单元也会开始形成一些区块,其结果称为一次聚集(primary clustering),就是说,散列到区块中的任何关键字都需要多次试选单元才能够解决冲突,然后该关键字被添加到相应的区块中。
平方探针
平方探测是消除线性探测中一次聚集问题的冲突解决方法。平方探测就是冲突函数为二次的探测方法。流行的选择是f(i)=i**2。图5-13显示与前面线性探测例子相同的输人使用该冲突函数所得到的散列表。
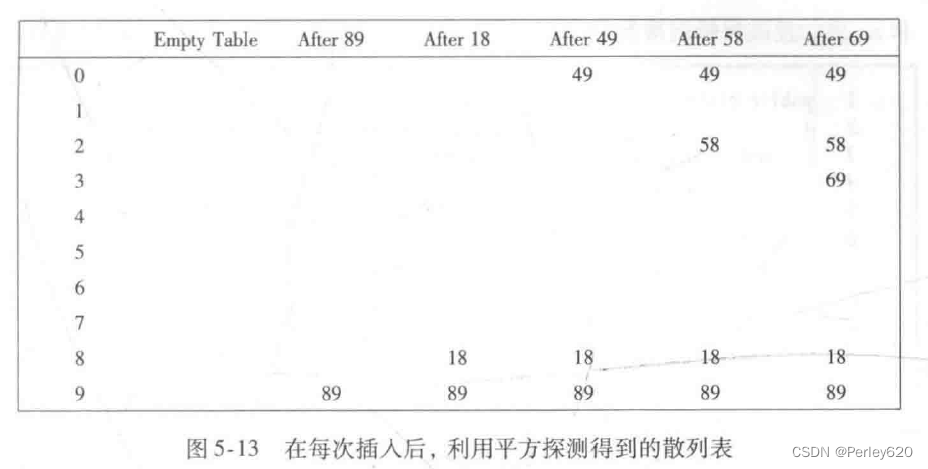
当49与89冲突时,其下一个位置为下一个单元,该单元是空的,因此49就被放在那里。此后,58在位置8处产生冲突,其后相邻的单元经探测得知发生了另外的冲突。下一个探测的单元在距位置8为2=4远处,这个单元是个空单元。因此,关键字58就放在单元2处。对于关键字69,处理的过程也一样。
虽然平方探测排除了一次聚集,但是散列到同一位置上的那些元素将探测相同的备选单元。这叫作二次聚集(secondary clustering)。二次聚集是理论上的一个小缺憾。模拟结果指出,对每次查找,它一般要引起另外的少于一半的探测。下面的技术将会排除这个缺撼,不过这要付出计算一个附加的散列函数的代价。
双散列(double hashing)

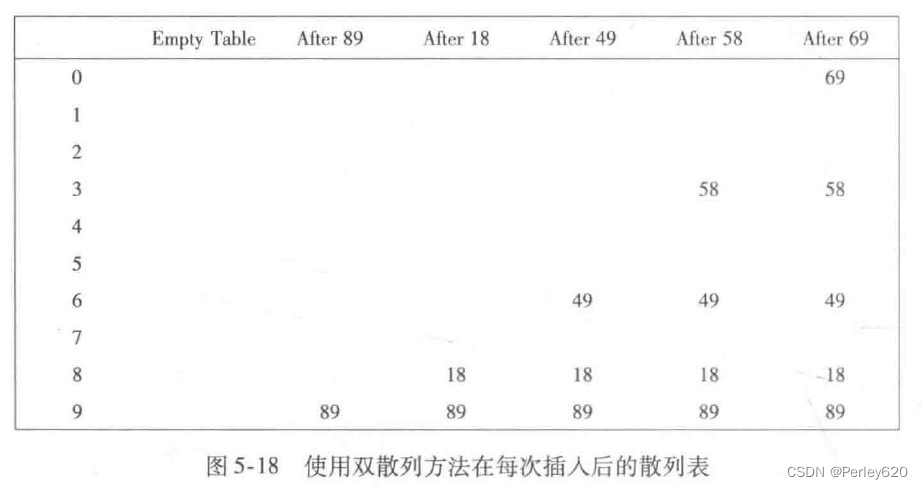
我们将要考察的最后一个冲突解决方法是双散列(double hashing)。对于双散列,一种流行的选择是f(i)=i·hash2(x)。这个公式是说,我们将第二个散列函数应用到x并在距离hash2(x),2hash(x),…等处探测。hash2(x)选择得不好将会是灾难性的。例如,若把99插入到前面例子中的输入中去,则通常的选择hash2(x)=xmod9将不起作用。因此,函数一定不要算得0值。另外,保证所有的单元都能被探测到也是很重要的(但在下面的例子中这是不可能的,因为表的大小不是素数)。诸如hash2(x)=R-(x mod R)这样的函数将起到良好的作用,其中R为小于TableSize的素数。如果我们选择R=7,则图5-18显示插入与前面相同的一些关键字的结果。
第一个冲突发生在49被插入的时候。hash2(49)=7-0=7,故49被插入到位置6。hash2(58)7-2=5,于是58被插人到位置3。最后,69产生冲突,从而被插入到距离为hash2(69)=7-6=1远的地方。如果我们试图将60插入到位置0处,那么就会产生一个冲突。由于hash2(60)=74=3,因此我们尝试位置3、6、9,然后是2,直到找出一个空的单元。一般是有可能发现某个坏
Java标准库中的散列表
标准库包括Set和Map的散列表的实现,即HashSet类和HashMap类。HashSet中的项(或HashSet中的关键字)必须提供equals方法和hashCode方法,如较早我们在节5.3所描述的那样。HashSet和HashMap通常是用分离链接散列实现的。
如果这些表项是否可以依有序方式查看这一点并不重要,那么这些类可以使用。例如,在4.8节的单词变换例子中,存在三种映射:
1.其中关键字为单词长度(word length),而关键字的值是长为该单词长度的所有单词的集合。
2.关键字是一个代表(representative),而关键字的值是具有该代表的所有单词的集合。
3.关键字是一个单词(wod),而关键字的值是与该单词只有一个字母不同的所有单词的集合。
因为单词长度被处理的顺序并不重要,所以第1个映射可以是HashMap。而由于第2个映射建立以后甚至不需要代表,因此第2个映射也可以是HashMap。第3个映射还可以是HashMap,除非我们想要printHighChangeables依字母顺序列出单词的子集(这些单词可以被变换成许多其他单词)。
HashMap的性能常常优于TreeMap的性能,不过不按这两种方式编写代码很难有把握肯定。因此,在HashMap或TreeMap可以接受的情况下,更可取的方法是:使用接口类型Map进行变量的声明,然后,将TreeMap的实例变成HashMap的实例并进行计时测试。
在Java中,能够被合理地插人到一个HashSet中去或是所谓关键字被插入到HashMap中去的那些库类型已经被定义了equals和hashCode方法。
特别是String类中有一个hashCode方法。

总结
1.散列表,key,散列函数;
2.哈希冲突的解决;
3.string中的hashCode;




)





)

)


漏洞CVE-2020-5421)



