文章目录
- 题目
- 方法一:层序遍历 + 集合排序
- 方法二:中序遍历(栈 或者 递归 )
- 方法三(方法二改进):中序遍历(栈 )
题目
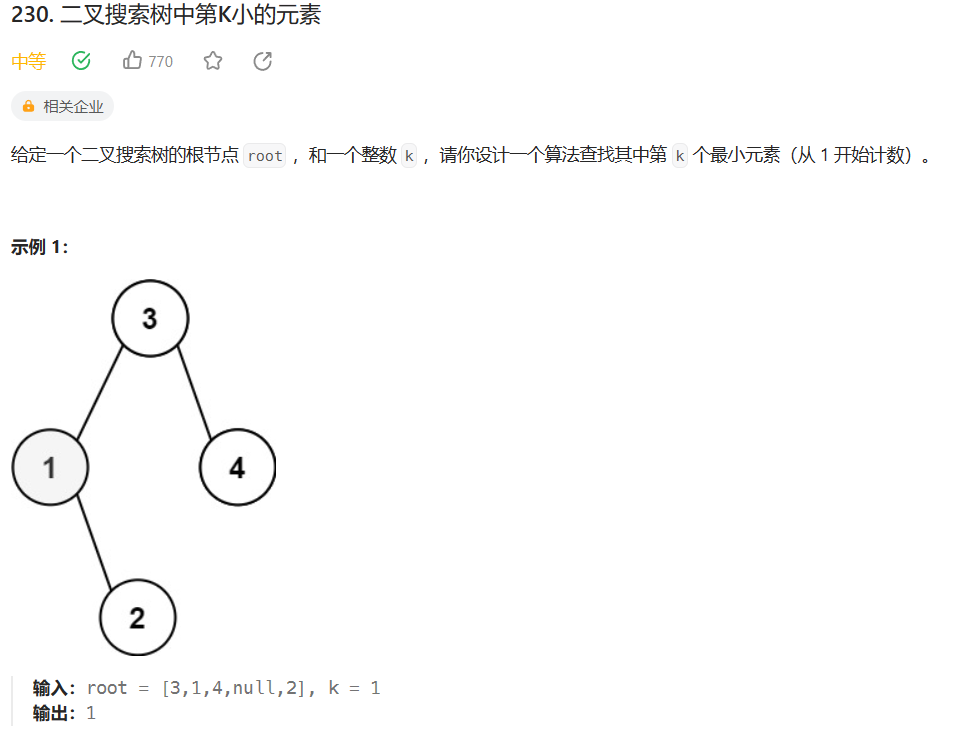
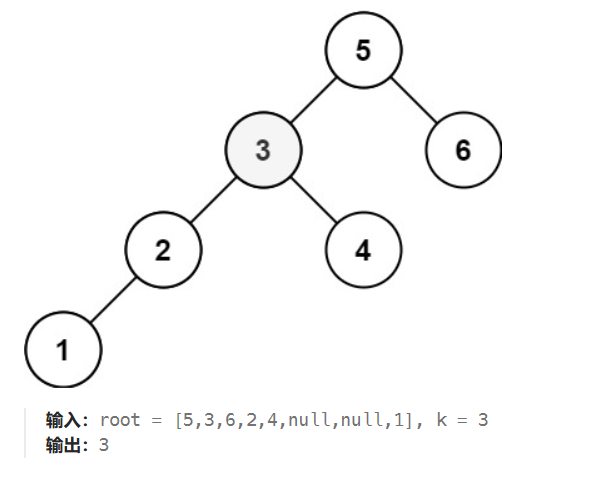
该题最大的特点就是这个树是二叉树:

所以,中序遍历对二叉树的遍历本身就是有序的
方法一:层序遍历 + 集合排序
思想很简单,就是通过层序遍历将节点都加到List集合中,然后调用 Collections.sort(list)排序后,找第k小的数list.get(k-1)
public int kthSmallest(TreeNode root, int k) {List<Integer> list = levelOrder(root);Collections.sort(list);return list.get(k-1);}public List<Integer> levelOrder(TreeNode root) {List<Integer> result = new ArrayList<>();Queue<TreeNode> queue = new LinkedList<TreeNode>();if(root == null) return result;queue.offer(root);while(!queue.isEmpty()){int count = queue.size();for(int i =0 ;i< count ;i++){TreeNode node = queue.poll();result.add(node.val); if(node.left != null) queue.offer(node.left);if(node.right != null) queue.offer(node.right);}}return result;}
方法二:中序遍历(栈 或者 递归 )
二叉树中序遍历得到的值序列是递增有序的 借助一个list集合来接收有序的节点 然后再按照k去list集合区第k小的数
List<Integer> list =new ArrayList<>();public int kthSmallest(TreeNode root, int k) {// dfs(root); //递归中序stackTree(root); // 栈中序return list.get(k-1);}//递归中序// public void dfs(TreeNode root) {// if(root == null ) return ;// dfs(root.left);// list.add(root.val);// dfs(root.right);// }// 栈中序public void stackTree(TreeNode root) {Deque<TreeNode> stack = new ArrayDeque<TreeNode>();while(!stack.isEmpty() || root != null){while(root != null){stack.push(root);root = root.left;}root = stack.pop();list.add(root.val);root = root.right;}}
方法三(方法二改进):中序遍历(栈 )
二叉树中序遍历得到的值序列是递增有序的 那只要栈每次弹出一个元素时 就让k-1(直到k=0) 例如要第1小的数 那么其实就是中序遍历栈弹出的第一个元素(k= k-1 ===0,立马返回第一次pop的数)
public int kthSmallest(TreeNode root, int k) {Deque<TreeNode> stack = new ArrayDeque<TreeNode>();while(!stack.isEmpty() || root != null){while(root != null){stack.push(root);root = root.left;}root = stack.pop();k--;//每弹出一个元素,就让k--if(k == 0) return root.val;//直到k减到0 说明该root.val就是第k小的数root = root.right;}return -1;})

)


漏洞CVE-2020-5421)




![服务器安装 anaconda 及 conda: command not found [解决方案]](http://pic.xiahunao.cn/服务器安装 anaconda 及 conda: command not found [解决方案])
利用opencv调用鼠标事件在图像上绘制图形)

)





