LangChain这个词今年已经听烂了，今天基于昇腾的角度总结一下：

Why LangChain ？

场景：构建一个LLM应用

在构建一个新项目时，可能会遇到许多API接口、数据格式和工具。要去研究每一个工具、接口很麻烦。

假设要构建一个智能聊天机器人，难道要一步步去学习如何训练一个语言模型，如何处理各种数据，还要解决所有的兼容性问题吗？

这就是LangChain的价值所在

LangChain是一个集成框架，提供一系列的工具和组件，使能语言模型中各种数据（如Google Analytics、Stripe、SQL、PDF、CSV等）的连接、语言模型的应用和优化，一切将简单直接。

————————————————————————————————————————————————————————————
LangChain好比一把“瑞士军刀”，不再需要为每一个任务找一个新工具，提供一站式解决方案。

正如要修理一个小家用电器，而你已经拥有一个完整的工具箱。不管遇到啥问题，打钉子、拧螺丝、剪线，工具箱里总有一个合适的工具。

LangChain提供了这样的工具箱，不仅涵盖了基础工具，还为个性化需求提供了自定义组件解决方案。

正是因为LangChain连接了开发者和复杂的LLM应用，因此，开发变得更为简单、高效。越来越多的开发者，不论是LLM领域的还是非LLM领域的，都选择使用LangChain。

现代软件工程宗旨：将庞大复杂的系统划分为更小、更易于管理和使用的部分

LangChain以**“组件”** 和 **“链”**作为2个关键概念，为LLM应用开发者提供了便利。

• 组件 不是代码的拼凑，而是一个具有明确功能和用途的单元。组件包括LLM模型包装器、聊天模型包装器及与数据增强相关的一系列工具和接口。这些组件就是LangChain中的核心，你可以把它们看作数据处理流水线上的各个工作站。每个组件都有其特定的职责，如处理数据的输入输出、转化数据格式。

• 链 是将各种组件连接在一起的纽带，它能够确保组件之间的无缝集成和在程序运行环境中的高效调用。无论是对于LLM还是其他工具，链都扮演着至关重要的角色。举个例子，LLMChain，这是LangChain中最常用的链，它可以整合LLM模型包装器和记忆组件，让聊天机器人拥有“记忆”。

向量数据库

向量数据库（Vector Database）可高效存储和处理非结构化的数据，如文档、图片、视频、音频和纯文本等。

在信息完整的情况下，通过向量的嵌入函数来精准描写这些非结构化的数据的特征，从而实现向量搜索、查询、删除、修改、元数据过滤等功能。

向量数据库的核心是将文本、图片、音频等非结构化的信息转换成向量的形式存储在数据库中，当用户输入问题时，将问题转换成向量，最后在数据库中搜索最相似的向量和上下文，最后将结果返回给用户。

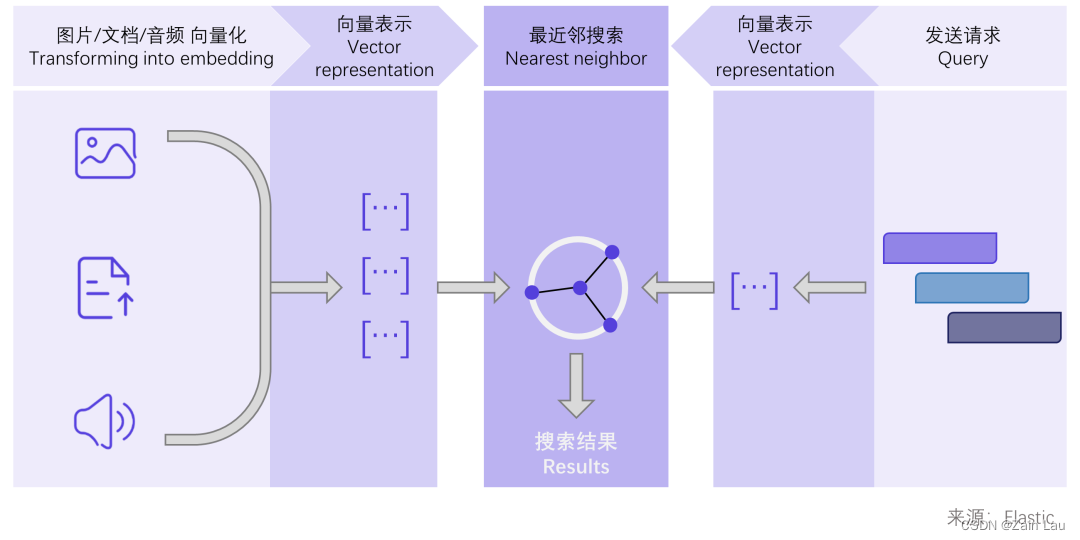
向量数据库和传统数据具有相似性，通过提供标准的sql访问接口，降低用户的使用门槛，同时提供高效的数据组织，检索和分析的能力。满足用户在存储和检索向量需求的同时，提供管理结构化数据的能力。

两者最大的区别在于传统数据库是一个精准的索引，查找到的内容存在正确答案，在数据库中的数据只有两类，一类是符合查询要求，可返回给用户；另一类则是不符合查询要求；而向量搜索则是一种模糊匹配，找到的是相对最符合需求的数据，而非一个精确的标准答案。

向量数据库依据保存和检索的不同可分为以下5类：

1）纯向量数据库：如Pinecone、Weaviate、Qdrant、Chroma、Zilliz、Vespa等专用于存储和检索向量，具有利用索引技术进行高效的相似性搜索，大数据集和查询工作负载的可扩展性，支持高维数据、基于HTTP和JSON的API，以及对向量运算（加法、减法、点积、余弦相似度）的原生支持等优点。

2）向量库：如Faiss、Annoy等，支持面相ANN的索引结构，包括倒排文件、乘积量化和随即投影，支持推荐系统、图片搜索和自然语言处理（NLP）。

3）全文搜索数据库：如Elastic、OpenSearch等，对于非结构化文本具有高扩展性和性能以及丰富的文本检索功能。

4）支持向量的非关系型（NoSQL）数据库：如DataStax、Cassandra、Rockset、MongoDB等，NoSQL数据库性能高、规模大。Neo4j（图形数据库）可与社交媒体或知识图谱的大语言模型融合。

5）支持向量的关系型（SQL）数据库：如ClickHouse、Singlestore、PostgreSQL等，多模型SQL数据库提供混合搜索，可将向量与其他数据结合，并且大多数SQL数据库可在云上部署服务。

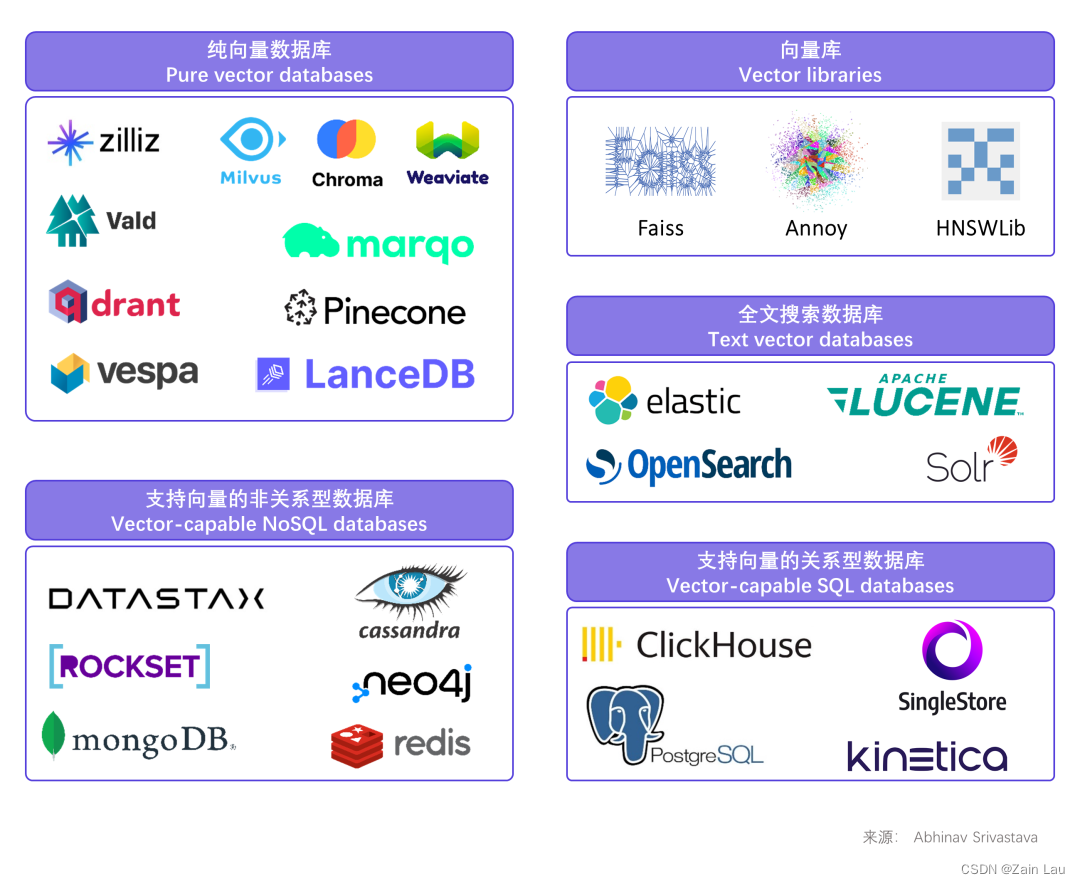
非结构化的信息以向量的形式存储在向量数据库中

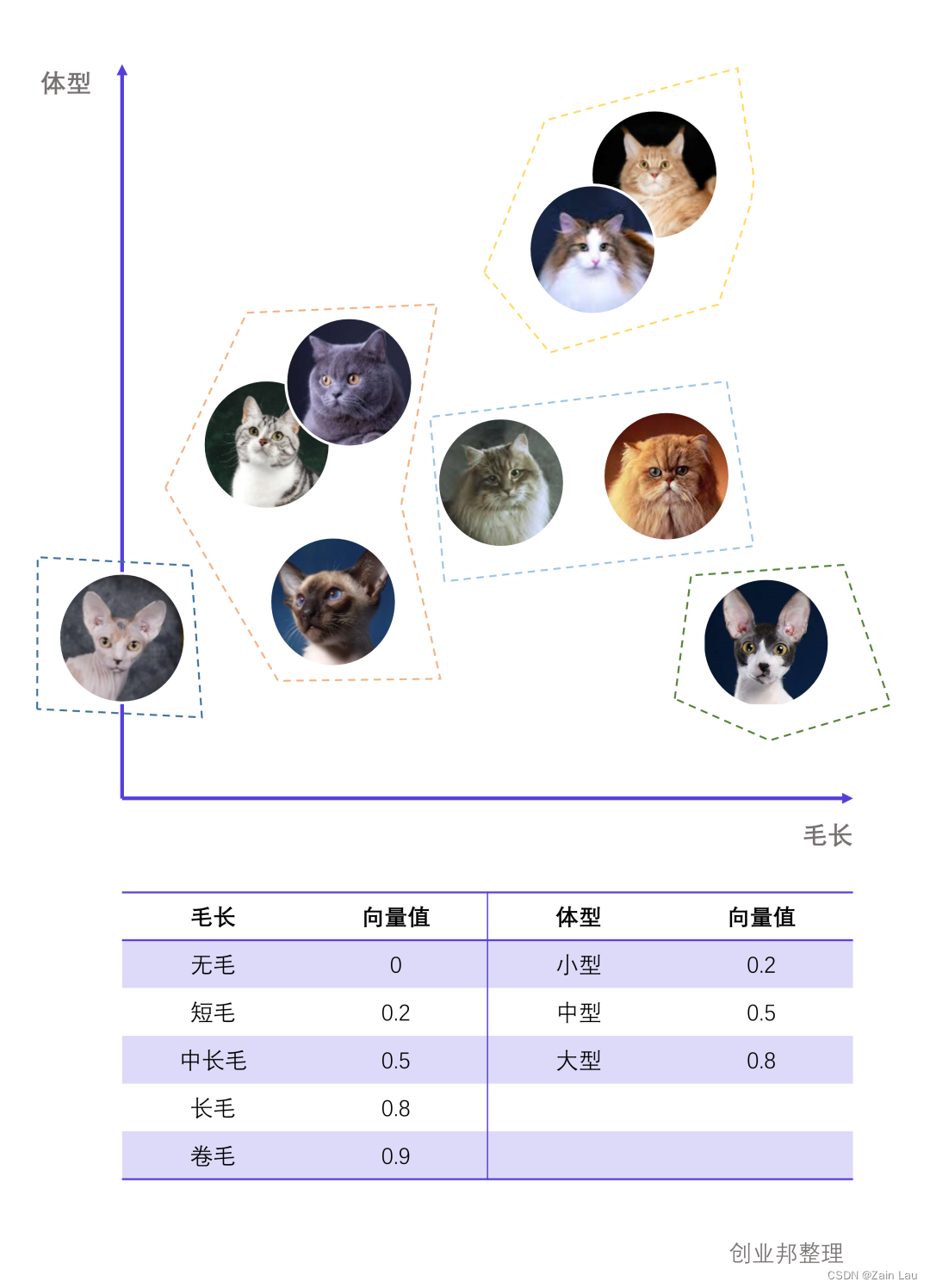
以猫为例，不同种类的猫可通过体型大小、毛发长度、腿长短等特征来区分。
下图中X-Y轴分别对应毛长和体型的数值，每只猫即可对应一个二维坐标点，由此可轻易将波斯猫、缅因猫和无毛猫区分开来，但仍然无法很好的区分波斯猫和西伯利亚猫。
通过继续添加腿的长短这一特征，得到一个三维的坐标系以及每只猫在三维坐标系中的位置，只要特征足够多就可以得到高维的坐标系。

向量是具有大小和方向的数学结构，将这些特征转化为向量表示，通过计算各向量之间的距离来判断它们的相似度，从而实现相似性搜索。

随着ChatGPT的发布，人工智能的发展迎来了新的时代，知识的存储与表达也有了新的标准，但其输入端上下文（tokens）大小的限制困扰着很多的开发者和消费者。

文本本身直接作为数据具有维度高、学习低效的缺点，因而大模型接触和学习的数据并非文本本身，而是向量化的文本，即大模型对自然语言的压缩和总结。

向量数据库是高维度的，可弥补生成式人工智能模型的这一缺陷。向量数据库通常用于支持复杂的查询操作，如相似性搜索，这种高效的索引和检索机制使向量数据库特别适用于机器学习和人工智能应用，提供强大的“记忆”能力。