首发于Data Science
单变量微分(Differentiation)
常用基本微分有:
四则运算法则:
链式法则(Chain-rule)
极大值(maxima)与极小值(minima)
向量微分
梯度下降(Gradient descent):几何直觉
学习率(Learning Rate)的直观理解
案例:线性回归的梯度下降法
随机梯度下降 (Stochastic gradient descent)
单变量微分(Differentiation)
微分指:当 x 发生变化时, y 改变多少(或变化率)
y 对 x 的微分可以写为 dydx=df(x)dx=y′=f′(x)

图一
切线的斜率可以表示为:ΔyΔx=y2−y1x2−x1=tanθ (θ 切线与 x 轴的夹角)
当 Δx→0 时, ΔyΔx=dydx ,极限公式可以为 dydx=limΔx→0ΔyΔx
常用基本微分有:

图二
四则运算法则:

图三
链式法则(Chain-rule)
令: f(g(x))=(a−bx)2
微分有: ddxf(g(x))=dfdg∗dgdx
假定: g(x)=(a−bx)=z ,那么 f(x)=f(z)=z2 , dfdg=dfdz=2z=2(a−bx)
那么 dgdx=(a−bx)′=−b
最终: ddxf(g(x))=dfdg∗dgdx=2(a−bx)∗(−b)
极大值(maxima)与极小值(minima)

图四
- 斜率(微分 dydx )为 0时,存在极大值或极小值
- 一个函数中,可以有多个局部极大值或极小值,但是只能有一个 全局极大值或极小值
但是,大多数函数都不能轻易 dydx=0 计算得出,所以将使用 梯度下降 来解决优化问题
向量微分
向量的微分得到一个向量,当 x 是向量时,求微分表示为:∇xf(x)=df(x)dx
案例: f(x)=y=a→Tx→=∑i=1naixi=a1x1+a2x2+⋯+anxn
- ai 为常数
∇xf(x)=[∂f∂x1∂f∂x2∂f∂x3⋮∂f∂xn]=[a1a2a3⋮an]=a→
- ∂f∂xi 表示元素的偏微分
梯度下降(Gradient descent):几何直觉
迭代算法;一开始我们对解决方案进行猜测,然后通过解决方案的修正迭代地走向解决方案;
当到达最优时,斜率为零

图五
- 随机选一点 x0 ,在 x0 处进行微分 [dfdx]x0 ,也就等于斜率
- x1 就等于 x1=x0−r[dfdx]x0 , r 指的时学习率(在此为例方便理解,可以看着为常数 1)
- x2 就等于 x2=x1−r[dfdx]x1
- 重复迭代 xi+1=xi−r[dfdx]xi,如果 xi+1−xi 时非常得小,那么在 xi≈x∗ , xi 存在极小值
小结: [dfdx]x0≥[dfdx]x1≥[dfdx]x2≥⋯ ,因为斜率的逐渐变小,所以 xi 变化得距离,也会越来越小
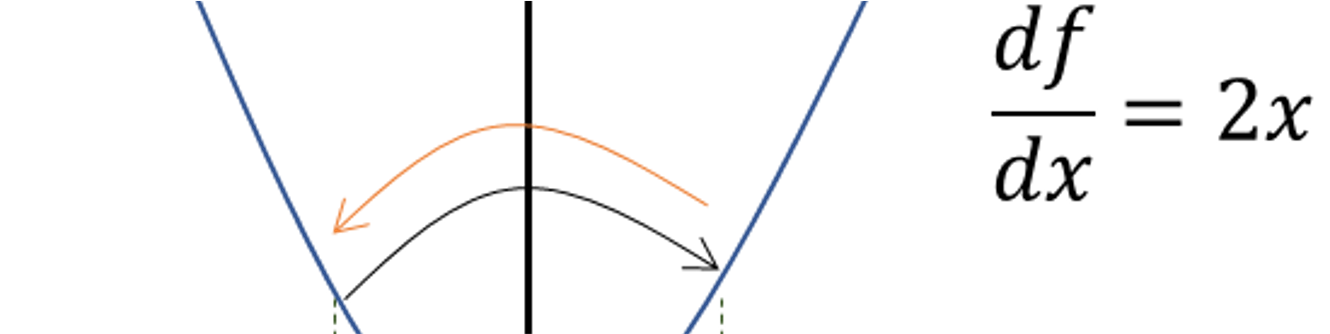
学习率(Learning Rate)的直观理解

图六
假设 xi,xi+1 的微分(斜率)都为 2x ,学习率 r=1
- xi+1=xi−r[dfdx]xi=0.5−1∗(2∗0.5)=−0.5
- xi+2=xi+1−r[dfdx]xi+1=−0.5−1∗(2∗(−0.5))=0.5
- 会发现点 xi+2=xi ,又回到原来的位置,而无法继续收敛
小结:如果学习率不降低,梯度下降可以跳过最优值,那么迭代没有达到最优值;一直来回振荡没有收敛;应该减小学习率,即在每次迭代时减小学习率,以保证收敛。
案例:线性回归的梯度下降法
线性回归的损失函数有: L(w→)=∑i=1n(yi−w→Tx→i)2
损失函数微分有: ∇wL=∑i=1n2(yi−w→Tx→i)(−x→i))
- 随机生成一个权重向量 w→0
- 迭代一次: w→1=w→0−r∑i=1n2(yi−w→0Tx→i)(−x→i))
- 迭代二次:w→2=w→1−r∑i=1n2(yi−w→1Tx→i)(−x→i))
- 依次迭代 k+1次,当 w→k+1−w→k 的变化非常小(基本可以忽略),那么权重先来 w→k 存在极小值,也就是最小的损失值
小结:在此的 n 表示的时训练集的样本量的大小,所以如果把所有的元素用来进行微分计算,也就是公式: ∑i=1n2(yi−w→Tx→i)(−x→i)) ,那么计算相当的大,因此有了随机梯度下降
随机梯度下降 (Stochastic gradient descent)
在上述讨论了线性回归的损失函数,利用梯度下降算法求解最优权重向量 w→ ,那么更新公式有:
梯度下降 GD: w→j+1=w→j−r∑i=1n2(yi−w→jTx→i)(−x→i))
随机梯度下降 SGD:w→j+1=w→j−r∑i=1k2(yi−w→jTx→i)(−x→i))
- 将 所有样本元素n 的迭代改为 k ,计算 k 个随机点,这样的梯度下降称为随机梯度下降( 1≤k≤n )
- 当 k=1 时,被称为 SGD, k>1 时经常被称为 batch SGD
- 当 k 越大时,迭代次数越少就能找到极值
- 在 随机梯度 过程中,每次迭代时, k 的样本元素集,都应该随机重新选择
- 在梯度下降中添加了随机性,以减少运行时的时间复杂度(同时在满足迭代次数足够的情况下,SGD 与 GD 的结果一样)
求导工具:https://www.derivative-calculator.net
)


二)



:Linux的常用命令)











)