原理
理想低通滤波器(Ideal Low-Pass Filter, ILPF)是数字图像处理中一个重要的概念,尤其在频率域滤波中扮演着关键角色。
定义:
理想低通滤波器是一种在频率域内工作的滤波器,旨在通过允许低频信号通过同时阻止高频信号来平滑图像。
它在频率域中通常表示为一个中心为原点的圆形区域。
工作原理:
图像首先通过傅里叶变换从空间域转换到频率域。
在频率域内,理想低通滤波器定义了一个截止频率,该频率确定了保留低频成分的区域大小。位于圆形内部(半径小于截止频率)的频率成分被保留,而圆形外部的高频成分被阻断。
截止频率:
截止频率是确定滤波器效果的关键参数。截止频率越低,滤波效果越强,导致图像更加平滑,但同时可能丢失更多的细节。
相反,较高的截止频率会保留更多的高频信息,但滤波效果减弱。
应用效果:
理想低通滤波器能有效去除图像中的噪声和高频细节,使图像变得更加平滑。
但它也可能引入一些不希望的效果,如振铃效应,这是由于其在截止频率处突然变化的特性所导致。
局限性:
理想低通滤波器因其在截止频率处的非自然过渡而不常用于实际应用。这种突然的过渡会导致图像中出现人造的振铃效应。
在实际应用中,通常会选择更平滑的低通滤波器,如高斯低通滤波器,以获得更自然的图像过渡效果。
应用领域:
虽然理想低通滤波器在实际图像处理中的应用受限,但它在理论学习和教育中仍然非常重要,帮助我们理解频率域滤波的基本概念。理想低通滤波器提供了一个基础框架,用于理解如何在频率域内操作图像,以及如何通过频率分析来影响图像的视觉内容。尽管在实际应用中可能更倾向于使用其他类型的低通滤波器,理解理想低通滤波器的基本原理仍然是学习数字图像处理的重要组成部分。
编写代码,
输出如下图所示的结果:
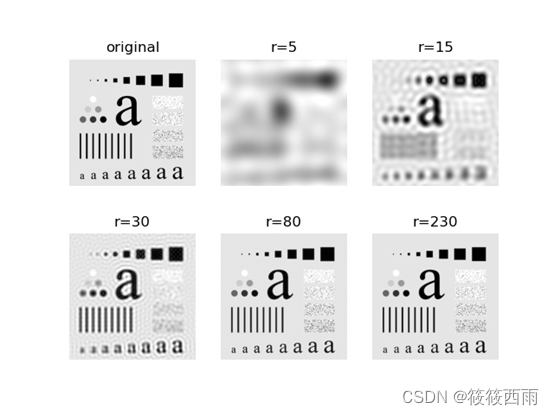
提示
结果显示了理想低通滤波器截止频率分别为5,15,30,80,230时的滤波结果。首先对图像做傅里叶变换并中心化其频谱。接着生成不同截止频率的理想低通滤波器,公式参考课本上公式5.29,需要注意的是,在计算D(u,v)时,不能直接用书上的公式计算(u,v)和原点(0,0)的距离,由于频谱经过了中心化,频率中心已经平移到了(M/2,N/2),所以要计算(u,v)到(M/2,N/2)的距离。最后,如公式5.28所示,将图像频谱与生成的理想低通滤波器传递函数H(u,v)相乘,再做去中心化和傅里叶反变换,便可以得到滤波后的图像。可以观察半径较小的ILPF的模糊效果和振铃特性。注意,np.fft.ifft2得到的是复数阵列,需要用np.abs取其幅度得到最终的图像。此外,滤波后的图像中会出现像素值超过255的情况,plt.imshow会自动调整灰度图的值域范围,所以为了正确显示图像,需要在imshow时加上参数vmin和vmax,如:axs[i, j].imshow(img, vmin=0, vmax=255, cmap=‘gray’)
import cv2
import numpy as np
import matplotlib.pyplot as pltimg=cv2.imread("Fig0441.tif",0)rows,cols=img.shapeDFT=np.fft.fft2(img)
center=np.fft.fftshift(DFT)H=np.zeros((rows,cols))
img_list=[img]
img_name_list=["original"]for n in [5,15,30,80,230]:for i in range(rows):for j in range(cols):D=np.sqrt(np.power((i-rows/2),2)+np.power((j-cols/2),2))if D<=n:H[i,j]=1else:H[i,j]=0G=np.multiply(H,center)no_center=np.fft.fftshift(G)g=np.abs(np.fft.fft2(no_center))img_list.append(g)img_name_list.append("r="+str(n))
_,axs=plt.subplots(2,3)for i in range(2):for j in range(3):axs[i,j].imshow(img_list[i*3+j],vmin=0,vmax=255,cmap="gray")axs[i,j].set_title(img_name_list[i*3+j])axs[i,j].axis('off')plt.show()结果展示

总结
做法流程:首先对图像做傅里叶变换并中心化其频谱。接着生成不同截止频率的理想低通滤波器,在计算D(u,v)时,不能直接用书上的公式计算(u,v)和原点(0,0)的距离,由于频谱经过了中心化,频率中心已经平移到了(M/2,N/2),所以要计算(u,v)到(M/2,N/2)的距离。最后,,将图像频谱与生成的理想低通滤波器传递函数H(u,v)相乘,再做去中心化和傅里叶反变换,便可以得到滤波后的图像。可以看到,半径越小,图片越模糊。
低通滤波器容许低频信号通过, 但减弱(或减少)频率高于截止频率的信号的通过。对于不同滤波器而言,每个频率的信号的减弱程度不同。当使用在音频应用时,它有时被称为高频剪切滤波器, 或高音消除滤波器。一个理想的低通滤波器能够完全剔除高于截止频率的所有频率信号并且低于截止频率的信号可以不受影响地通过。实际上的转换区域也不再存在。一个理想的低通滤波器可以用数学的方法(理论上)在频域中用信号乘以矩形函数得到,作为具有同样效果的方法,也可以在时域与sinc函数作卷积得到。








)



)






