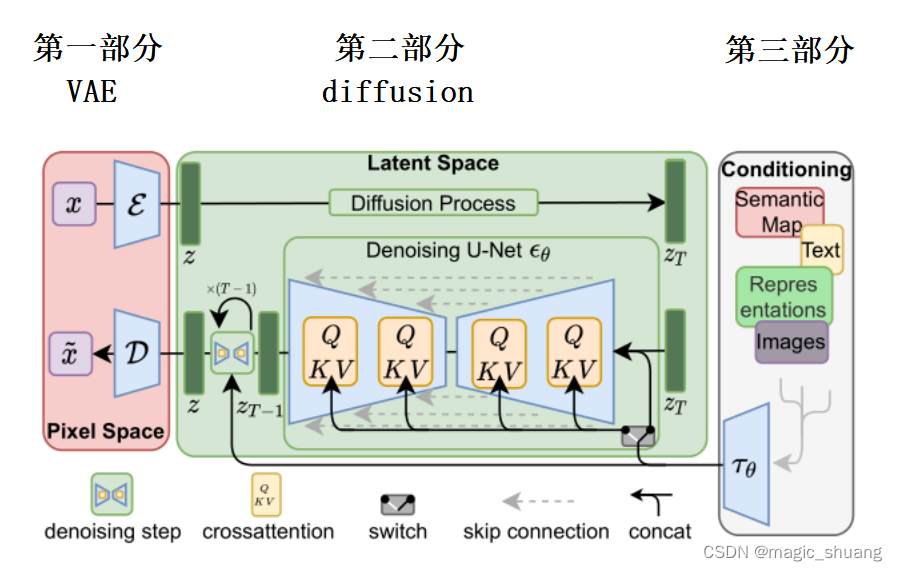
了解整个流程:
- 【第一部分】输入图像 x (W*H*3的RGB图像)
- 【第一部分】x 经过编码器
生成
(latent 空间的表示) h*w*c (具体设置多少有实验)
- 【第二部分】
逐步加噪得到
,和噪声标签
- 【第二部分】由 Unet(
) 预测噪声与噪声标签得到loss, 训练
- 【第三部分】由 Clip 得到 文本编码或者图像编码 。以改变K和V的方式添加到Unet
- 【第二部分】训练后, Unet( 随机高斯 ,文本等条件)得到 z
- 【第一部分】解码器D将 z 重建成RGB图像
本文将分为3个部分讲解生成模型全过程:
- 第一部分:VAE 编码器
- 第二部分:diffusion 扩散模型
- 第三部分:多模态提示,微调
第一部分:VAE
代码:https://github.com/AntixK/PyTorch-VAE
论文:Auto-Encoding Variational Bayes
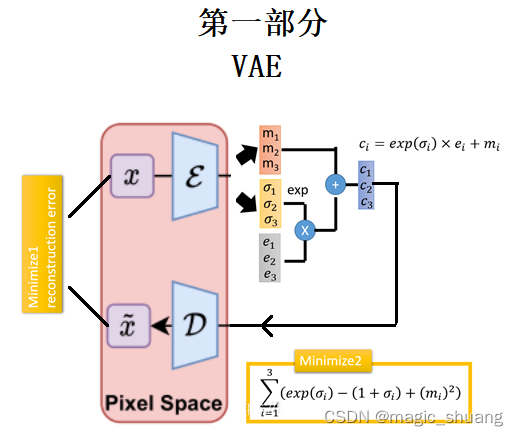
如图所示是VAE部分的训练过程:
- 图像编码得到 均值 (m1,m2,m3),方差(σ1,σ2,σ3),
- exp(σi)的目的是为了保证这个预测的方差是个正值,
- 按标准正态分布随机生成采样点(e1,e2,e3),重参数后相当于用预测出的高斯分布随机采样
- VAE在encode层的输出结果(c1,c2,c3)。
- 以(c1,c2,c3)重建原图
- 重建原图和原图计算MSE loss
- 外加惩罚项loss,使得预测分布接近标准正态分布
VAE的原理推导及代码
对于生成模型而言,主流的理论模型可以分为:
- 隐马尔可夫模型HMM
- 朴素贝叶斯模型NB
- 高斯混合模型GMM,而VAE的理论基础就是高斯混合模型。
什么是高斯混合模型呢?就是说,任何一个数据的分布,都可以看作是若干高斯分布的叠加。

代码实现 GMM 模型
VAE foreward:
def forward(self, input: Tensor, **kwargs) -> List[Tensor]:mu, log_var = self.encode(input)# mu : (B,128) 均值# log_var :(B,128) 方差z = self.reparameterize(mu, log_var) # 重参数return [self.decode(z), input, mu, log_var] # 解码从代码可以看出来,mu 和 log_var 就是上图的若干个高斯分布,可以由均值和方差生成任意位置概率值
其中,重参数定义如下:
def reparameterize(self, mu: Tensor, logvar: Tensor) -> Tensor:std = torch.exp(0.5 * logvar)eps = torch.randn_like(std) # 返回与输入张量大小相同的张量,其中填充了均值为0 方差为1 的正态分布的随机值z = eps * std + mureturn z可以看到,为每一对均值方差,都生成个随机采样
正态分布->标准正态分布: y = ( x - mu ) / std
标准正态分布-> 正态分布: x = y * std + mu
解码网络根据若干个高斯分布参数和 随机的样本 x 得到最终的原图
VAE decoder代码:
def decode(self, z: Tensor) -> Tensor:"""Maps the given latent codesonto the image space.:param z: (Tensor) [B x D]:return: (Tensor) [B x C x H x W]"""result = self.decoder_input(z)result = result.view(-1, 512, 2, 2)result = self.decoder(result)result = self.final_layer(result)return result损失:两部分(重建损失和KL损失)
kld_weight = kwargs['M_N'] # Account for the minibatch samples from the datasetrecons_loss =F.mse_loss(recons, input)
kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp()))loss = recons_loss + kld_weight * kld_loss公式推导
通过本部分的学习可以明白以下问题:
- 为什么是随机采样高斯分布上的点重建原图?
- 为什么是kl loss?
- 为什么kl loss 复杂表达式怎么来的?
如下图:
- 隐变量 z, 观测数据 x ,
是 生成模型参数 ,
是预测的分布参数;
- 实线表示生成模型
,
- 虚线表示难以处理的后验
的变分近似
- 变分参数φ与生成模型参数θ联合学习
- 隐变量 z (
)由一些先验分布 pθ 生成;
- x(
),从一些条件分布 pθ(x|z) 生成

我们通过能观测到的数据x,预测实际的分布参数z,采用最大似然函数的方法:
最大似然函数:样本 (公式省略参数
)
取log:
当似然函数取得最大值时,=
为所求
实际网络中函数是非凸函数,通过解析的方式直接求解非常困难,因此采用迭代的方法逐步逼近最大值。那么这个迭代的方法称为EM算法(最大化期望),给定的训练样本
样例间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。因此表达式就变成如下:
EM是一种两步迭代的方法:
1、初始化对参数
进行一次猜测
2、通过这个
得到 最大似然 的新表达---期望步骤
3、对这个新表达,求解最大值---------------最大化步骤
当迭代的数据量是一张图时,n=1时:
初始化一个参数 。(为了表示方便就不按迭代取名了) 根据EM算法,最大似然 的新表达:
拆成3部分后:
最后最大似然函数,求分布的参数。变成使得等式右边最大值时
分布的参数。
等号右边第三个等式:,近似值与真实后验值的KL散度,KL散度大于0。剩余部分是下界,最大值问题又变成最大下界问题。
等号右边第一个等式: 反映自动编码器的(Auto-Encoder-Decoder)性能: xi→z→xi,即经过编码
和 解码
的概率最大化,如果能重建的越好说明这部分取值最大,因此这部分就是Loss1MSE。
等号右边第二个等式: 是两个分布的相似度,分布q是 预测的高斯分布 , 分布p是标准正态分布,这部分越小,两个分布越相似,最终的似然函数越大。这部分就是Loss2 kl惩罚项。
- q~N(u,σ^2)
- p~N(0,1)
等号右边第一个式子:是常数项,是概率积分×常数
等号右边第二个式子:可以拆成三个不同的期望求解
由于高斯分布的一阶矩、二阶矩表达式如下:
代入上式:
等号右边第三个式子:可以看到就是二阶矩,因此:
代入三部分的化简,最后KL散度的值为:
到此,KL散度的loss推导结果:
对比代码部分:完全一致
kld_loss = torch.mean(-0.5 * torch.sum(1 + log_var - mu ** 2 - log_var.exp()))-----------------------------------------------------vae end----------------------------------------
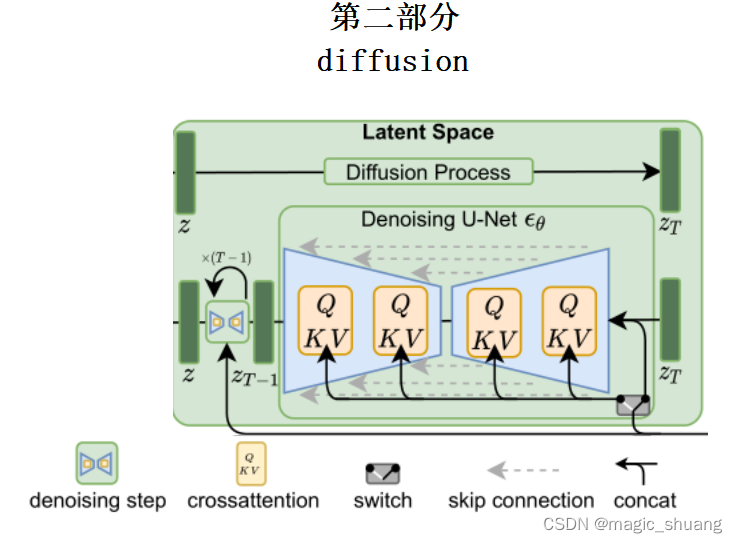
第二部分:扩散模型
论文:https://arxiv.org/abs/2112.10752
代码:GitHub - CompVis/latent-diffusion: High-Resolution Image Synthesis with Latent Diffusion Models
本部分分两个模块讲解
- 训练阶段
- 推理生成阶段
- 网络结构
2.1 训练阶段
由VAE编码器得到高维特征z,扩散模型训练、推理的维度都在这个空间进行
如下图所示,是把z逐渐加噪的过程

有加噪系数 随着加噪次数增多加噪力度也越来越大,实际代码
取值范围[0.00001,0.002]
z 加噪到第 t 次 ,特征变成 Xt,它是由Xt-1生成的,表达式如下:
可以看到,由于 越来越大
越来越小,也就是 Xt-1影响权重越来越小,噪音权重越来越大。
由于这个逐步加噪的过程都是常数,因此可以直接生成某次加噪的结果和噪音标签。但是具体怎么生成呢?
其中:噪声 是均随机采样自 标准正态分布 N(0,1).
因此:
服从 N( 0,
)
服从 N( 0,
)
看原式后两项,是两个分布相加,就是一个新的高斯分布 N( 0, ) 化简后:N( 0,
) 换成由标准正太分布表示的形式:
,带回原式子:
一直的递归下去,直到x0,可以得到:其中z是标准正态分布做的随机噪声
那么这个 就是我们想得到的任意时刻的加噪图片。
因此,训练流程:
repeat:
1、数据集采样
2、随机选取一个时刻 t (1~2000)
3、制作标签: t 时刻 图像上加的噪声 ~N(0,1)
4、计算梯度,由如下损失: 是噪声预测网络
2.2 生成过程
现在再看逆向的过程:由 逐渐得到
,扩散模型的预测噪声是一步一步预测的,也就是一步一步 逆向 先看由
到
,那么由概率表示就是
,而我们已知
,因此对其进行贝叶斯替换后:(第一行省略x0方便理解)
其中:等式右边的概率均可由前向推理表达出来,一切均由x0得到,上面第一行省略条件x0,由于下式子的展开需要用到x0因此不省略了
就是迭代加噪:
,服从
由
前向加噪到
:
,服从
由
前向加噪到
:
,服从
因此逆向的 ,就可以由三个高斯分布重新表示:
由于已知三个高斯分布的均值和方差,因此其概率密度就可以表示出来,带回到原贝叶斯公式:
可以看到等号右边的所有exp前都有常数项,因此上面等式可以化简为,正比于:
其中C是常数项,不用管。
对于任意高斯分布都有:
通过平方项和一次项参数求解 均值&方差 因此:
令为
; 令
为
上面得到分布 的均值和方差,可以看到均值里面包含
,由于推理阶段
是未知的,但是可以由
表达出来:
由
得到,逆向一下,那么
也可以由
表示:
将 重新代入均值表达式:
到此 的均值和方差都是已知的了,使用重采样方法得到 x t-1,其中z~N(0,1)
将均值和方差代入:(方差是固定值,暂时由σ表示)
到此已经得到所有公式的推导。
因此,推理流程:
1、随机生成个高斯噪声 ~N(0,1),噪声预测模型
2、 for t in [T,T-1,......1]:
z ~N(0,1) if t>1 else z=0
3、return
下图理解起来更容易:

网络结构
噪声预测模型的网络结构总体是UNet的形状,其中的block是crossAttention
去噪的过程就是重复执行Unet,逐步降噪

具体网络结构如下:

可以看到每个block都有次数 t 的位置编码加入,本来代表加噪次数的 t 在模型中是正余弦位置编码

上图是Unet网络中的Time Embedding & crossAttention,可以看到代表次数的位置编码Time Embedding是通过线性变换后直接加到原特征图上。
下图是具体的Block结构
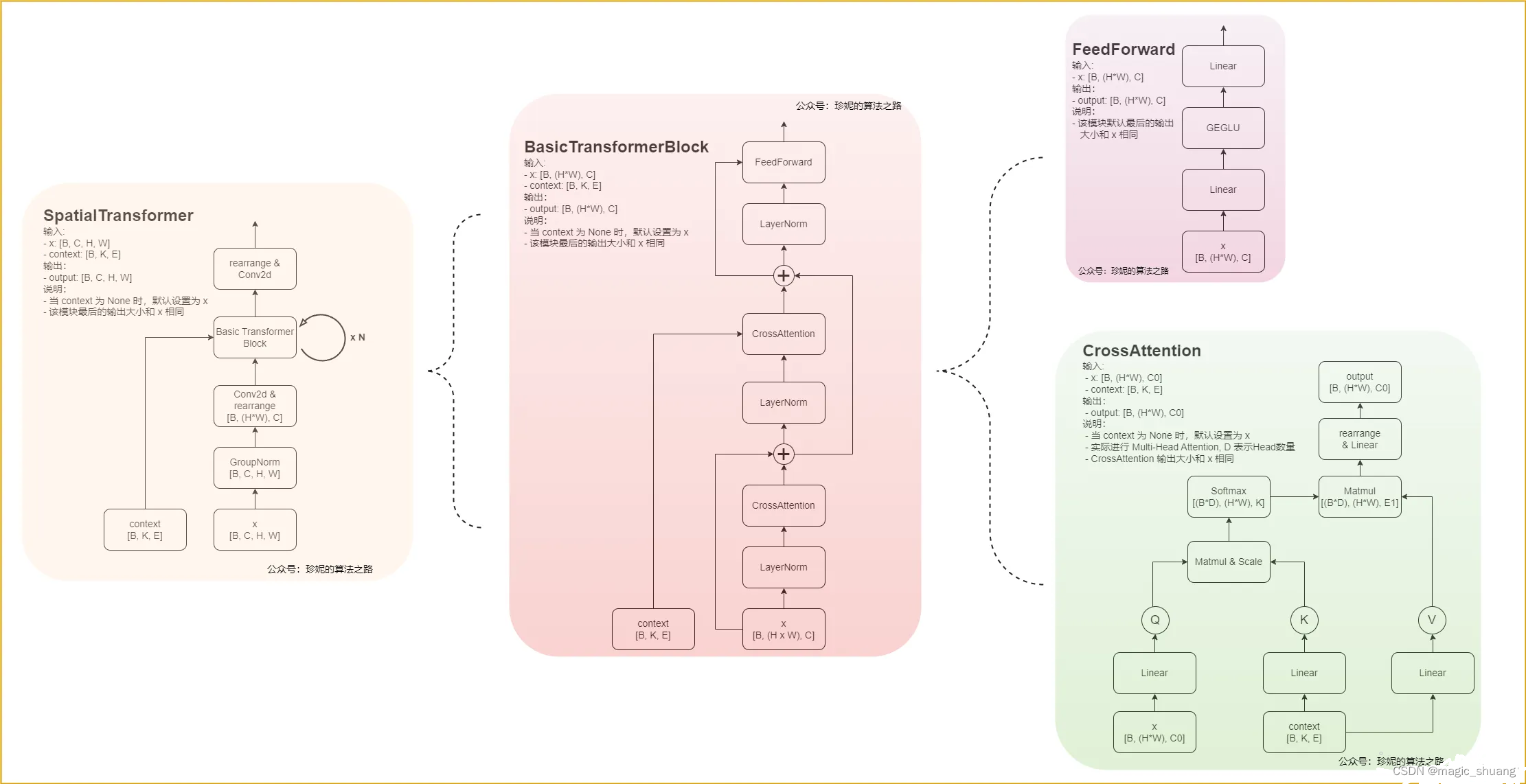
第三部分: 微调方法

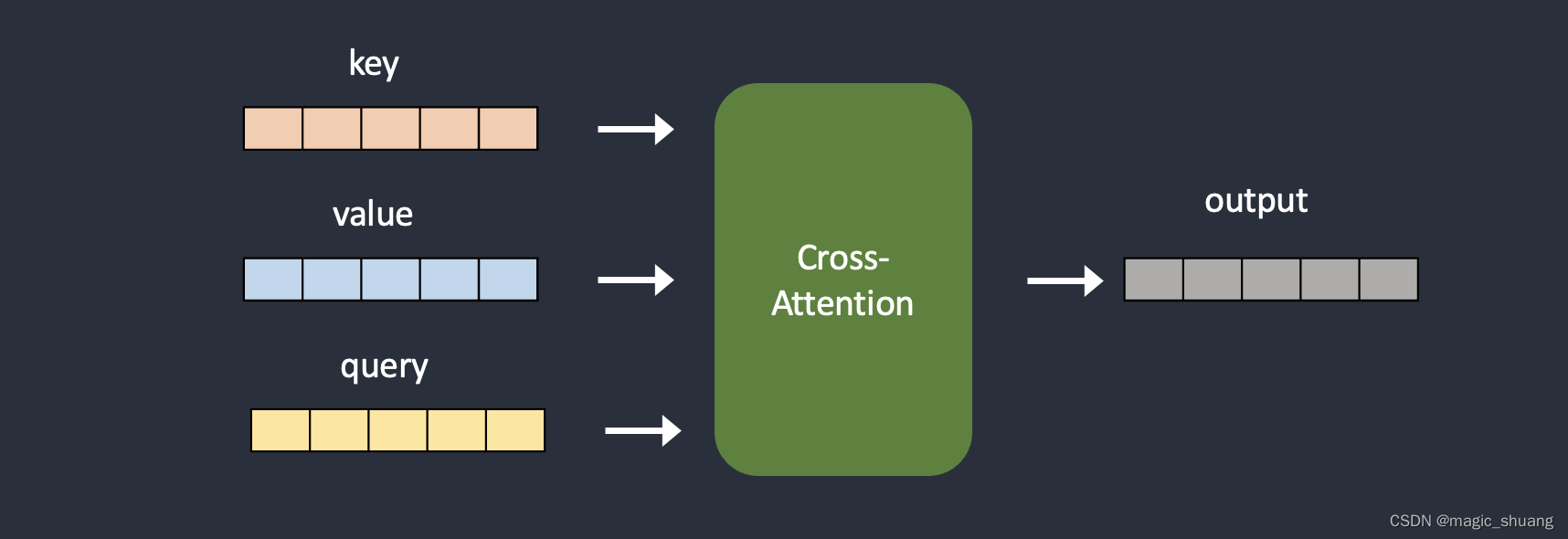
上图可以看出其他模态的数据&条件均通过交叉注意力中的K和V添加进网络
四种模型训练方法:
- Textual Inversion(Embeddings):只训练成对的目标词语和图像,其他部分全部冻结
- Hypernetwork:附加到Diffusion model的小型神经网络,用于修改其风格
- LoRA:(Low-Rank Adaptation of Large Language Models) 改变权重来修改交叉注意力
- DreamBooth:几张图像进行训练来更新整个扩散模型
Textual Inversion(Embeddings)
代码:GitHub - rinongal/textual_inversion
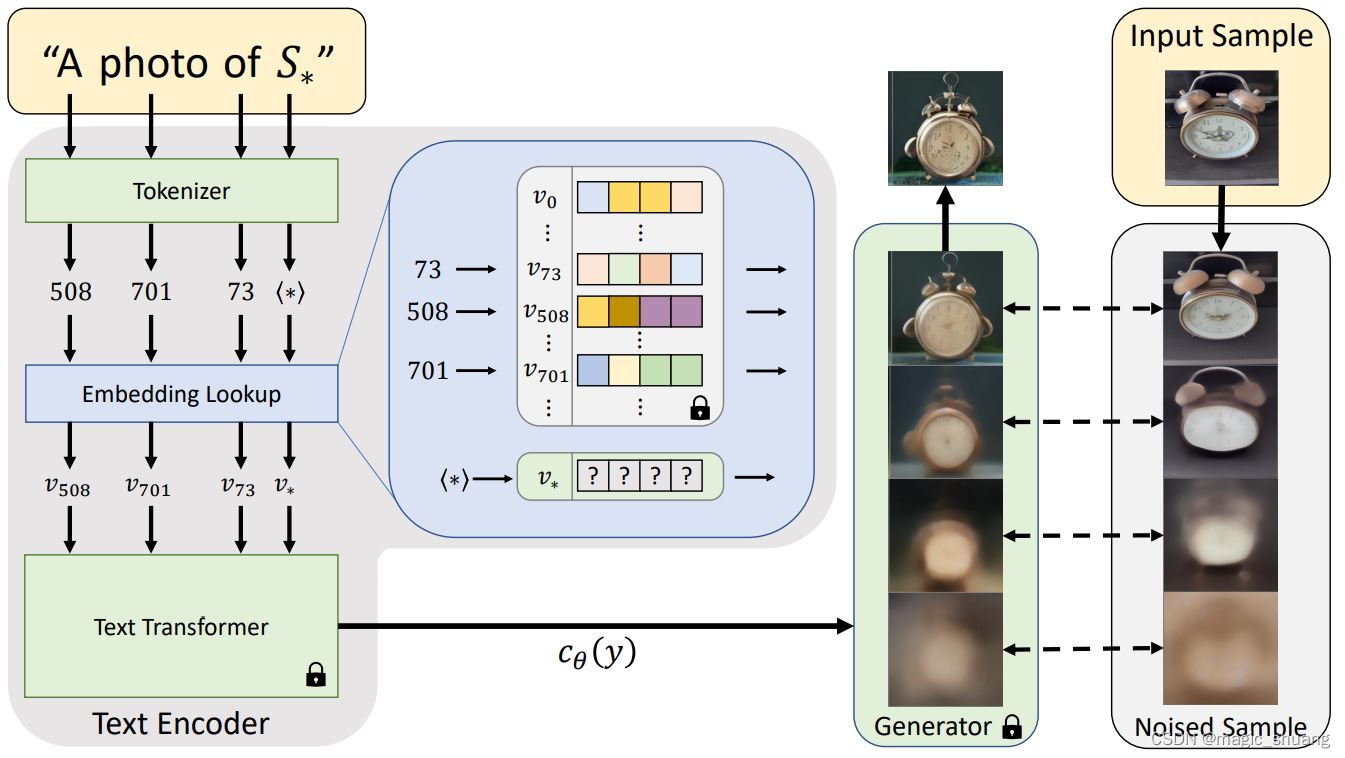
# 训练:如图,少量图像 和 新的词语 成对微调网络,其他词语冻结
# 这样就可以使用模型原有的能力在我们提供的图像类别上了,风格角度等等
python main.py --base configs/latent-diffusion/txt2img-1p4B-finetune.yaml -t --actual_resume /path/to/pretrained/model.ckpt -n <run_name> --gpus 0, --data_root /path/to/directory/with/images # 训练集图像--init_word <initialization_word> # 初始化提示词注释:
txt2img-1p4B-finetune.yaml 配置文件中的↓ 需要修改placeholder_strings: ["*"] # 为训练集图像类别initializer_words: ["sculpture"] # 初始化提示词推理时,可以使用文字提示 "a photo of *" 来生成图像
通常适用于转换图像风格
模型关键字尽量是不常见的词语Hypernetwork
它是一个附加到Stable Diffusion model的小型神经网络,用于修改其风格。

# 训练过程中 原本的stable Diffusion冻结不训练
# 仅训练 Hypernetwork-1&Hypernetwork-2
# 大约几十MB
# 通常训练艺术风格
# 推荐训练画风
LoRA
LoRA 模型类似Hypernetwork,它们都很小并且只修改交叉注意力模块。区别在于他们如何修改它。 LoRA 模型通过改变权重来修改交叉注意力。超网络通过插入额外的网络来实现这一点。 用户普遍发现 LoRA 模型能产生更好的结果。它们的文件大小相似,通常低于 200MB,并且比检查点模型小得多。
DreamBooth
base:embeding改的:https://github.com/XavierXiao/Dreambooth-Stable-Diffusion
是一种训练技术,通过对某个主题或风格的几张图像进行训练来更新整个扩散模型。它的工作原理是将提示中的特殊单词与示例图像相关联。
作者希望将输入图片中的物体与一个特殊标识符绑定在一起,即用这个特殊标记符来表示输入图片中的物体。因此作者为微调模型设计了一种prompt格式:
a [identifier] [class noun]
即:将所有输入图片的prompt都设置成这种形式,
其中
- identifier 是一个与输入图片中物体相关联的特殊标记符,
- class noun 是对物体的类别描述。
这里之所以在prompt中加入类别,是因为作者想利用预训练模型中关于该类别物品的先验知识,并将先验知识与特殊标记符相关信息进行融合,这样就可以在不同场景下生成不同姿势的目标物体
作者提出的方法,大致如下图所示,即仅仅通过3到5张图片去微调文生图模型,使得模型能将输入图片中特定的物品和prompt中的特殊标记符关联起来。
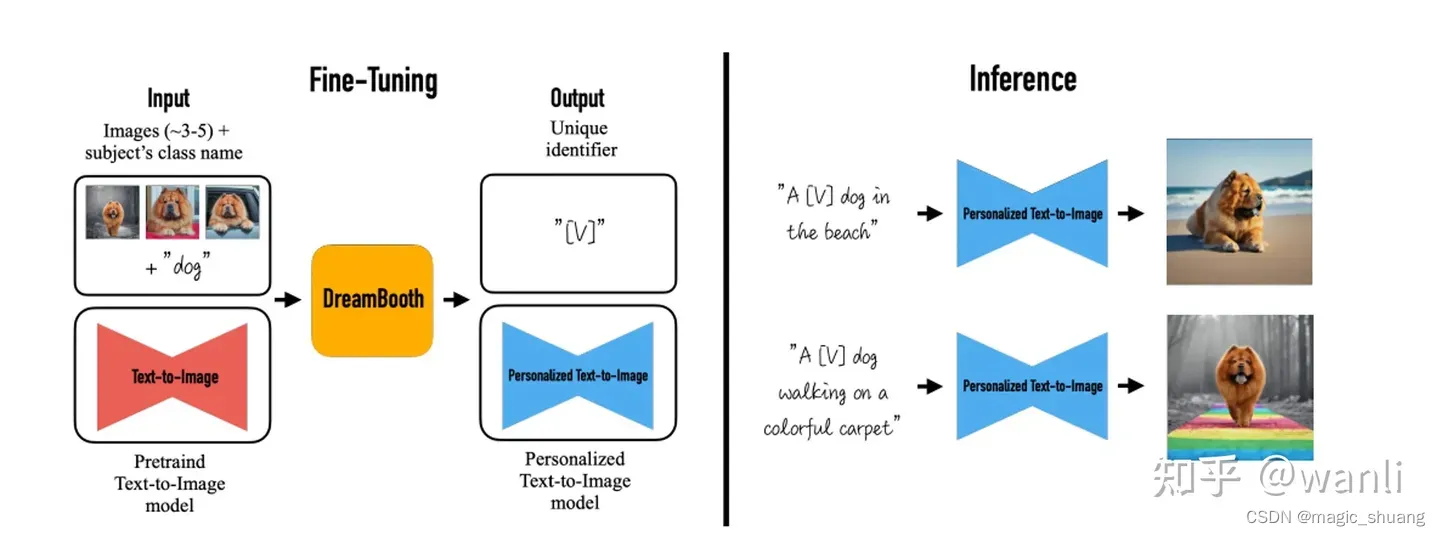
:Namespace详解)



)




)

)

)


:ClickHouse的分片集群)


