7.13N皇后（LC51-H）

算法：

N皇后是回溯的经典题

画树：

假设N=3

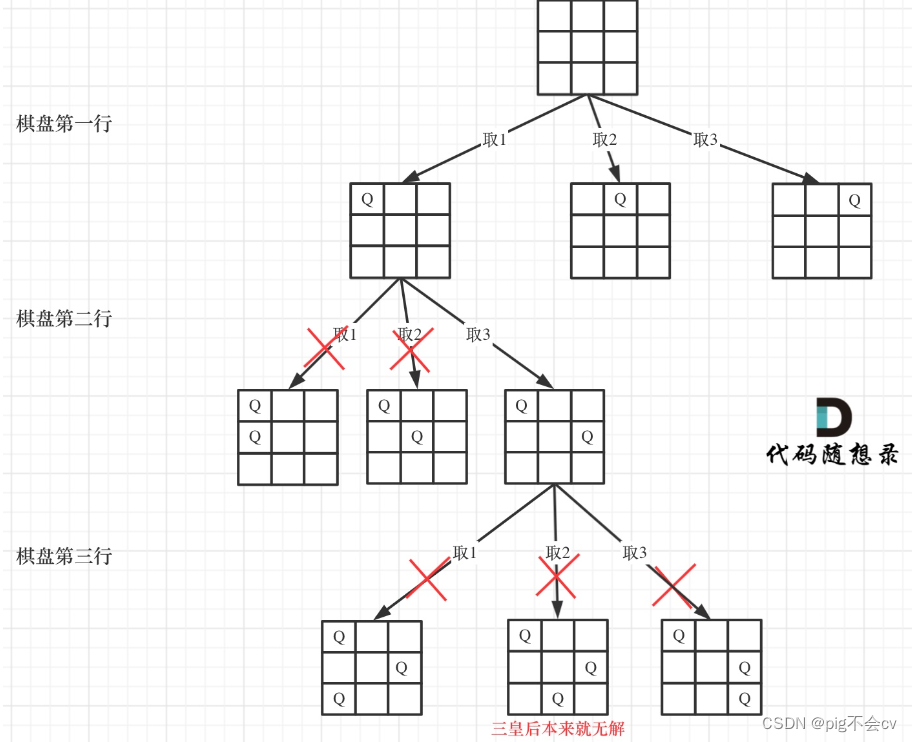
皇后们的约束条件：

不能同行
不能同列
不能同斜线

回溯三部曲：

1.确定函数参数和返回值

返回值：void

参数：

int n：题目给出，N皇后的个数，棋盘大小nxn

int row：用row来记录当前遍历到棋盘的第几层了

char[][] chessboard：二维字符数组，表示棋盘。每个`chessboard[i]` 都是一个字符数组，而`chessboard[i][j]` 则表示二维数组中特定位置 `(i, j)` 处的字符值。

2.确定终止条件

row==n

当递归到棋盘最底层（也就是叶子节点）的时候，就可以收集结果并返回了。

3.单层递归逻辑（for循环）

每次都是要从新的一行的起始位置开始搜，所以都是从0开始。

for (int col = 0;col < n; col++) {if (isValid (row, col, n, chessboard)) {// 验证合法就可以放chessboard[row][col] = 'Q';//递归backTrack(n, row+1, chessboard);//回溯，撤销皇后chessboard[row][col] = '.';}}

验证棋盘是否合法

isValid：先判错

按照如下标准去重：

不能同行
不能同列
不能同斜线（45度和135度角）

同列

for (int i = 0; i < row; i++) { // 这是一个剪枝if (chessboard[i][col] == 'Q') {return false;}}

同行（其实可以不放，因为在单层搜索的过程中，每一层递归，只会选for循环（也就是同一行）里的一个元素，所以不用去重了。）

for (int j = 0; i < col; j++) { // 这是一个剪枝if (chessboard[row][j] == 'Q') {return false;}}

同斜线（45度）

for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {if (chessboard[i][j] == 'Q') {return false;}}

同斜线（135度）

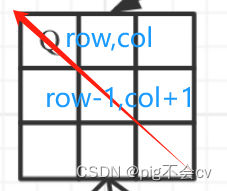
 for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {if (chessboard[i][j] == 'Q') {return false;}}

正确代码：

class Solution {List<List<String>> result = new ArrayList<>();public List<List<String>> solveNQueens(int n) {char[][] chessboard2 = new char[n][n];for (char[] c:chessboard2){Arrays.fill(c,'.');}backtracking(n, 0, chessboard2);return result;}void backtracking (int n, int row, char[][] chessboard){if (row == n) {result.add (Array2List(chessboard));return;}for (int col=0; col<n; col++){if (isValid(col, row, n, chessboard)) {chessboard[row][col] = 'Q';backtracking(n, row+1, chessboard);chessboard[row][col] = '.';}}}boolean isValid(int col, int row, int n, char[][] chessboard){//同列for (int i=0; i<row; i++){if (chessboard[i][col] == 'Q')  return false;}//同行for (int i=0; i<col; i++){if (chessboard[row][i] == 'Q') return false;}//45度for (int i=row-1, j= col-1 ; i>=0 && j>=0; i--, j--){if (chessboard[i][j] == 'Q') return false;}   //135度for (int i=row-1, j= col+1;  i>=0 && j<n; i--, j++){if (chessboard[i][j] == 'Q') return false;} return true; }List Array2List(char[][] chessboard) {List<String> list = new ArrayList<>();for (char[] c : chessboard) {list.add(String.copyValueOf(c));}return list;}}