目录

5-5 AVL出现的原因

5-5-1 平衡树

（1）设想如下场景：使用之前实现的BST，从空树开始向其中插入如下序列$n_1,n_2,...n_k$，且$n_{i-1}<n_i$，则会形成如下图所示的二叉树，其实已经退化成链表了：

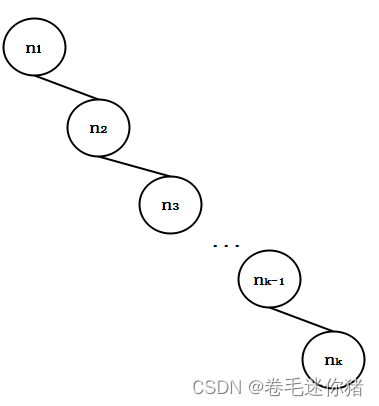
（2）同理，对删除操作，如果每次都删除树中的最小/最大key节点，那么一棵树也可能会退化成链表。
（3）对于链表，查询效率为$O(N)$，远不及BST原始设计时设想的$O(logN)$，即这种不平衡（左右两支节点的深度差异过大，有的节点查询深度过深）是需要改进BST数据结构来避免的。

【如何解决？】==> 保证insert/remove操作后树形结构的左右枝平衡即可（balance）。

【注】此处需要读者自学两个概念：“满树”、“完全树”，需要指出的是它们与平衡树的概念是有区别的。

5-5-2 平衡二叉树的具体案例

实现平衡不是一个简单的过程，但有很多策略/算法可以用于解决此问题，为此前人也创造了不少新的数据结构，譬如如下自平衡BST：
（1）AVL树（古老的入门平衡树）
（2）RBTree（红黑树，大名鼎鼎的通用树）
（3）Treap（树堆）
（4）AA树（红黑树变体）

当然，后续我们还要陆续讨论和实现例如：
（1）Trie（字典树）
（2）2-3树、2-3-4树
（3）k-d树
…
可以说树的知识点是很有分量的，清北的数据结构与算法课程中[1]，都安排了大量的时间去讨论相关内容，慢慢学，不着急。

5-6 AVL平衡策略的讨论

【摘自《数据结构与算法分析(C++描述)》】：AVL(Adelson-Velskii and Landis,由阿德尔森一维尔斯和兰迪斯在1962年提出,因此得名)树是带有平衡条件(balance condition)的二叉查找树。

（1）AVL需要通过保持平衡维持树的平均深度为$O(logN)$

（2）策略1：要求左右子树具有相同的高度。 ==> 这个策略限制条件过于严格了。

（3）策略2：要求左右子树高度相差最多为1。 ==> 这个策略更加实用。

【注】平衡二叉树不一定是具有$2^k-1$个节点的理想平衡树哦（perfectly balance tree）！
借用主线教材的一张图说明问题：

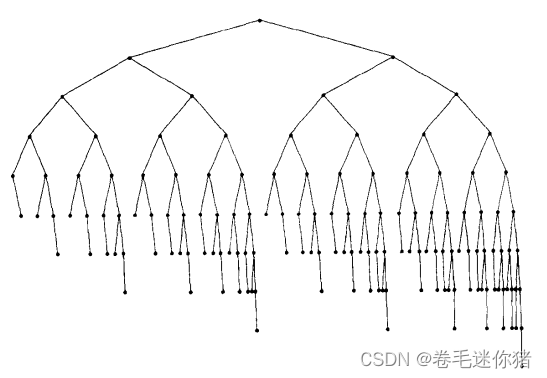
（4）我们定义空树的高度为-1，每次可能产生不平衡的操作无外乎两种：添加节点（insert）和删除节点（delete/remove），接下来看图讨论4种调整平衡的策略使得左右子树高度差不超过1（（$|height(left)-height(right)|⩽1$））：

【核心思想】找到根节点拎起来，根据BST节点的有序性，合理的挂上左右子树。

（a）LL型（k1<k2）

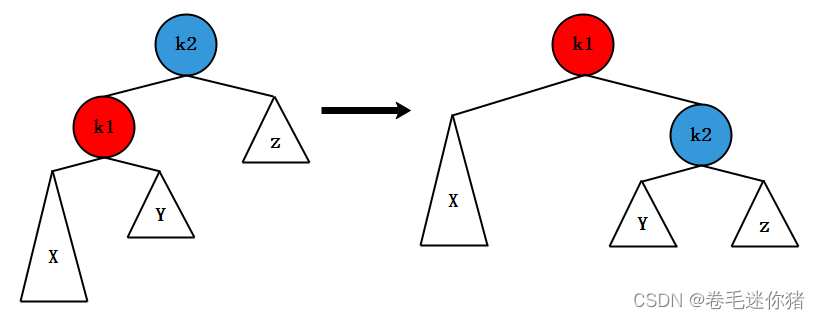
说明（参考《黑皮书》描述）：
<1> 节点k1<k2，目前不平衡的根因是k2的左枝即以k1为根节点的左子树不平衡（height(X) -height(Y) > 1）。
<2> 我们可以把k1节点拎起来做新的子树根节点，那k2节点自动往下掉。
<3> 此时k2自然成为k1的右枝，若需要维持平衡，那么原来k1的右子树（Y）就应该找一个地方挂上。
<4> 且Y子树所有节点都是大于k1的，Y当然只能放在k1的右枝；且Y中节点肯定都小于k2，自然就成为k2的新左子树啦。

以上过程往往被称为“单旋转”（single rotation），人们也会根据旋转的方向不同划分为“左旋转”和“右旋转”，甚至和后续提及的伸展树一样使用zig/zag的称谓，个人觉得初学者不用记那么多，自己能画图理解就行！

这个过程看似简单，在编码时注意操作节点left和right的指向即可，大致操作过程如下：
step1 暂存k1的右子树Y，因为接下来k1的右子树要被替换成k2；
step2 将k2挂在k1的右枝上；
step3 将step1中暂存的Y挂在k2的左枝上。
==> 完事！

（b）RR型（k1<k2）

如下图示，参考LL型做镜像处理（所以我们要先掌握BST的所有细节，特别是对着floor和ceil去写代码理解呢，哈哈哈，环环相扣！）（height(Z) -height(Y) > 1）

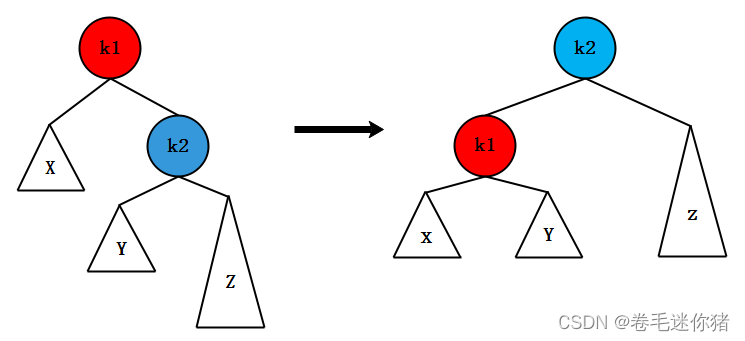
（c）LR型（k1<k2<k3）

很明显，这种情况仅靠一次旋转是无法实现平衡的我们可以采取以下策略：
step1 首先使用一次单边旋转（右旋），实现k1、k2的平衡，因为此时：height(k1_right) -height(k1_left) > 1
step2 把由k1、A、B组成的新树看做一个整体，即k2的新左子树，对k2、k3使用一次单边旋转（左旋），实现平衡。

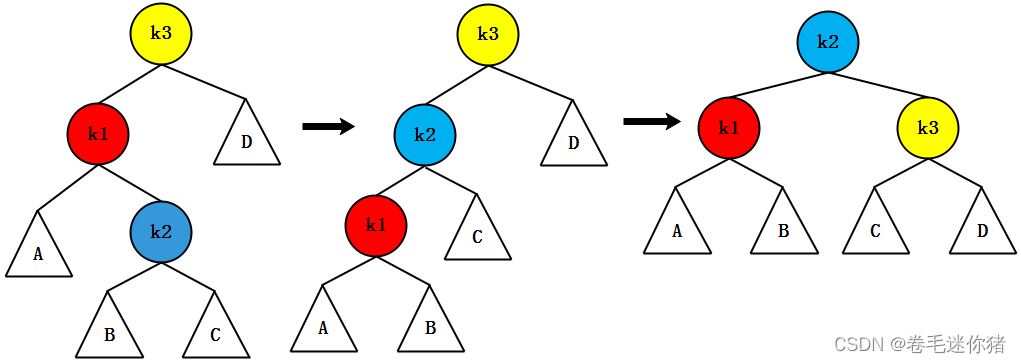
即使用两次单旋转，实现一次双旋转操作。

（d）RL型（k1<k2<k3）

同（3），镜像操作即可。

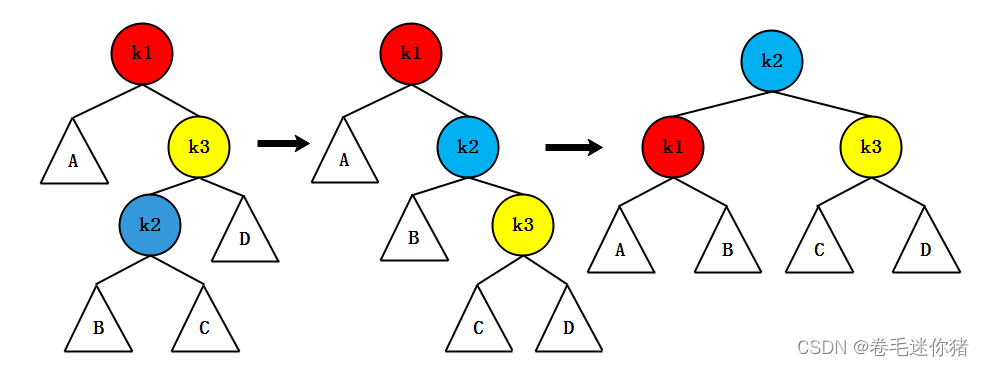
（5）更多的时候，人们会定义平衡因子（balance factor），在每次insert/delete操作后，再用平衡因子作为判定条件尝试平衡AVL树，这种思路能够大大降低编码实现难度，核心策略如下（参考[2]的描述）：

假设本来这棵树是平衡的，在我们在插入一个结点以后，导致了这棵树的不平衡，那么必然是这棵树根结点的平衡因子从 +1 变成了 +2，或者从 -1 变成了 -2 。实际上，总共有四种情况：
1）LL，根结点的平衡因子 +2，左子树根结点平衡因子 +1；
2）RR，根结点的平衡因子 -2，右子树根结点平衡因子 -1；
3）LR，根结点的平衡因子 +2，左子树根结点平衡因子 -1；
4）RL，根结点的平衡因子 -2，右子树根结点平衡因子 +1。

平衡因子（balance factor） BF= height(left) - height(right)

【注】
（1）此处的平衡因子等于+2或-2，其实也可写作大于1或者小于-1
（2）无论是否使用平衡因子，都需要在每个节点维护以当前节点为根的子树的高度；这点和之前讨论BST常规操作中，在节点中添加记录节点数量的域N非常类似。（咱们的教程真的是循序渐进的，一环扣一环，对新生很友好的好伐。）

5-7 不使用平衡因子的实现（黑皮书，训练思维）

我们依旧本着化繁为简的原则，在第一版简单BST的基础上修改代码实现AVL，不使用key作为比较依据。

（1）ADT（h头文件）

#ifndef _AVL_TREE 
#define _AVL_TREE
typedef int ElementType;struct AvlNode {ElementType Element;struct AvlNode *Left;struct AvlNode *Right;int Height;
};typedef struct AvlNode *AvlTree;AvlTree MakeEmpty(AvlTree T);
AvlTree Find(ElementType X, AvlTree T);
AvlTree FindMin(AvlTree T);
AvlTree FindMax(AvlTree T);
AvlTree Insert(ElementType X, AvlTree T);
AvlTree Delete(ElementType X, AvlTree T);
ElementType Retrieve(AvlTree T);
#endif

（2）简单的MakeEmpty和Find操作，无需多言

AvlTree MakeEmpty(AvlTree T){if(T != NULL){MakeEmpty(T->Left);MakeEmpty(T->Right);free(T);}return NULL;
}AvlTree Find(ElementType X, AvlTree T){if(T == NULL)return NULL;if(X < T->Element)return Find(X, T->Left);else if(X > T->Element)return Find(X, T->Right);else /* X == T->Element */return T;
}

（3）FindMin和FindMax，以及Retrieve

AvlTree FindMin(AvlTree T){if(T == NULL)return NULL;if(T->Left == NULL)return T;elsereturn FindMin(T->Left);
}AvlTree FindMax(AvlTree T){if(T == NULL)return NULL;if(T->Right == NULL)return T;elsereturn FindMax(T->Right);
}ElementType Retrieve(AvlTree T){return T->Element;
}

（4）定义求高度和比较大小常用操作

static int Height(AvlTree T){return (T == NULL) ? -1 : T->Height;
}static int Max(int a, int b){return a > b ? a : b;
}

注意空树高度为-1，因为节点结构中维护了高度值，所以只要在insert和delete环节及时更新一下就能方便使用了。

（5）4种旋转操作，对照之前的图文描述很容易实现/理解

/* 
* Assume node: K1 < K2 < K3
*/static AvlTree SingleRotateWithLeft(AvlTree K2){AvlTree K1 = K2->Left;K2->Left = K1->Right;K1->Right = K2;K2->Height = Max(Height(K2->Left), Height(K2->Right)) + 1;K1->Height = Max(Height(K1->Left), K2->Height) + 1;return K1;
}static AvlTree SingleRotateWithRight(AvlTree K1){AvlTree K2 = K1->Right;K1->Right = K2->Left;K2->Left = K1;K1->Height = Max(Height(K1->Left), Height(K1->Right)) + 1;K2->Height = Max(Height(K2->Right), K1->Height) + 1; // Max(Height(K2->Left), Height(K2->Right)) + 1; return K2;
}static AvlTree DoubleRotateWithLeft(AvlTree K3){K3->Left = 	SingleRotateWithRight(K3->Left);return SingleRotateWithLeft(K3);
}static AvlTree DoubleRotateWithRight(AvlTree K1){K1->Right = SingleRotateWithLeft(K1->Right);return SingleRotateWithRight(K1);
}

（6）插入操作，在原有BST的insert基础上修改，即插入成功后及时平衡；注意最后一步需要维护根节点的高度（这步带有非常明显的递归思路==>左+右+中）。

AvlTree Insert(ElementType X, AvlTree T){if(T == NULL){T = malloc(sizeof(struct AvlNode));if(T == NULL){printf("Create AVL Tree ERROR\n");exit(0);}T->Element = X;T->Height = 0;T->Left = T->Right = NULL;} else if(X < T->Element){T->Left = Insert(X, T->Left);if(Height(T->Left) - Height(T->Right) == 2){ // or > 1if(X < T->Left->Element) // or Height(T->Left->Left) > Height(T->Left->Right)return SingleRotateWithLeft(T);elsereturn DoubleRotateWithLeft(T);}} else if(X > T->Element){T->Right = Insert(X, T->Right);if(Height(T->Right) - Height(T->Left) == 2){if(X > T->Right->Element) // or Height(T->Right->Left) < Height(T->Right->Right)return SingleRotateWithRight(T);elsereturn DoubleRotateWithRight(T);}}T->Height = Max(Height(T->Left), Height(T->Right)) + 1;return T;
}

（7）同理，在原来BST的delete基础上完善平衡操作，注意要避开删掉叶子节点后的边界情况。

AvlTree Delete(ElementType X, AvlTree T){if(T == NULL){printf("Tree is null, delete fail\n");return NULL;}if(X < T->Element){T->Left = Delete(X, T->Left);if(Height(T->Right) - Height(T->Left) == 2){if(Height(T->Right->Left) > Height(T->Right->Right))return DoubleRotateWithRight(T);elsereturn SingleRotateWithRight(T);}} else if(X > T->Element){T->Right = Delete(X, T->Right);if(Height(T->Left) - Height(T->Right) == 2){if(Height(T->Left->Right) > Height(T->Left->Left))return DoubleRotateWithLeft(T);elsereturn SingleRotateWithLeft(T);}} else {AvlTree TmpCell;if(T->Left && T->Right){TmpCell = FindMin(T->Right);T->Element = TmpCell->Element;T->Right = Delete(T->Element, T->Right);} else {TmpCell = T;if(T->Left == NULL) // conbime leaf node case: Tl=TR=NULLT = T->Right;else if(T->Right == NULL)T = T->Left;free(TmpCell);}}if(T != NULL) // case: leaf node has been deleted!!!T->Height = Max(Height(T->Left), Height(T->Right)) + 1;return T;
}

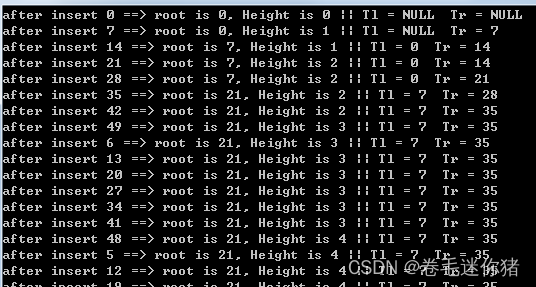
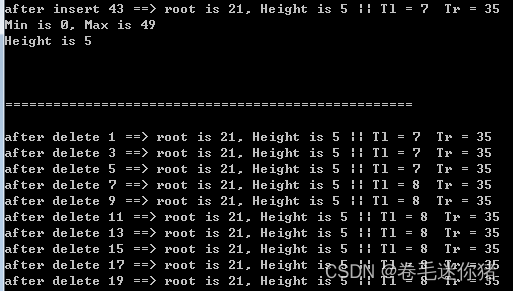
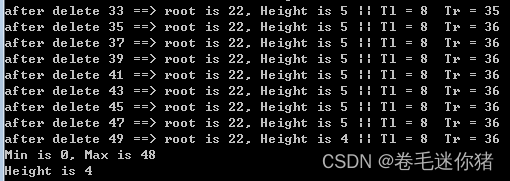
（8）测试代码和运行结果

#include <stdio.h>
#include <stdlib.h>
#include "AvlTree.h"int main(int argc, char *argv[]) {AvlTree T;AvlTree P;int i;int j = 0;T = MakeEmpty(NULL);for(i = 0; i < 50; i++, j = (j + 7) % 50 ){T = Insert(j, T);printf("after insert %d ==> root is %d, Height is %d || ", j, T->Element, T->Height);if(T->Left != NULL)printf("Tl = %d  ", T->Left->Element);elseprintf("Tl = NULL  ");if(T->Right != NULL)printf("Tr = %d  ", T->Right->Element);elseprintf("Tr = NULL");printf("\n");}for(i = 0; i < 50; i++)if((P = Find(i, T)) == NULL || Retrieve(P) != i)printf("Error at %d\n", i);printf("Min is %d, Max is %d\n", Retrieve(FindMin(T)), Retrieve(FindMax(T)));printf("Height is %d \n", T->Height);printf("\n\n\n===================================================\n\n");for(i = 1; i < 50; i += 2){T = Delete(i,T);printf("after delete %d ==> root is %d, Height is %d || ", i, T->Element, T->Height);if(T->Left != NULL)printf("Tl = %d  ", T->Left->Element);elseprintf("Tl = NULL  ");if(T->Right != NULL)printf("Tr = %d  ", T->Right->Element);elseprintf("Tr = NULL");printf("\n");}for(i = 0; i < 50; i += 2)if((P = Find( i, T )) == NULL || Retrieve(P) != i )printf( "Error at %d\n", i);for(i = 1; i < 50; i += 2)if((P = Find(i, T)) != NULL)printf("Error at %d\n", i);printf("Min is %d, Max is %d\n", Retrieve(FindMin(T)), Retrieve(FindMax(T)));printf("Height is %d \n", T->Height);return 0;
}

5-8 使用平衡因子的实现（更加常见的实现方法）

核心思想：先照常BST操作，完成insert和delete之后统一做一次balance，如果符合条件就真的执行旋转，否则不动。

（1）ADT，基本没有变化

#ifndef _AVL_TREE_2
#define _AVL_TREE_2
typedef int ElementType ;
struct AvlNode {ElementType Element;struct AvlNode *Left;struct AvlNode *Right;int Height;
};typedef struct AvlNode *AvlTree;AvlTree MakeEmpty(AvlTree T);
AvlTree Find(ElementType X, AvlTree T);
AvlTree FindMin(AvlTree T);
AvlTree FindMax(AvlTree T);
AvlTree Insert(ElementType X, AvlTree T);
AvlTree Delete(ElementType X, AvlTree T);
ElementType Retrieve(AvlTree T);
#endif

（2）具体实现，关注一下balance操作的位置和各种旋转的判定；相对上一小节的实现思路更加简单，所以很多人使用这一版。

#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include "AvlTree.h"AvlTree MakeEmpty(AvlTree T){if(T != NULL){MakeEmpty(T->Left);MakeEmpty(T->Right);free(T);}return NULL;
}AvlTree Find(ElementType X, AvlTree T){if(T == NULL)return NULL;if(X < T->Element)return Find(X, T->Left);else if(X > T->Element)return Find(X, T->Right);elsereturn T;
}AvlTree FindMin(AvlTree T){if(T == NULL)return NULL;return (T->Left == NULL) ? T : FindMin(T->Left);
}AvlTree FindMax(AvlTree T){if(T == NULL)return NULL;return (T->Right == NULL) ? T : FindMax(T->Right);
}ElementType Retrieve(AvlTree T){return T->Element;
}static int Height(AvlTree T){return (T == NULL) ? -1 : T->Height;
}static int Max(int a, int b){return a > b ? a : b;
}static void resetHeight(AvlTree T){if(T != NULL)T->Height = Max(Height(T->Left), Height(T->Right)) + 1;
}static int caculatelBF(AvlTree T){return (T == NULL) ? 0 : (Height(T->Left) - Height(T->Right));
}static AvlTree SingleRotateWithLeft(AvlTree K2){ //LLAvlTree K1 = K2->Left;K2->Left = K1->Right;K1->Right = K2;resetHeight(K2);resetHeight(K1);return K1;
}static AvlTree SingleRotateWithRight(AvlTree K1){ //RRAvlTree K2 = K1->Right;K1->Right = K2->Left;K2->Left = K1;resetHeight(K1);resetHeight(K2);return K2;
}static AvlTree DoubleRotateWithLeft(AvlTree K3){  //LRK3->Left = 	SingleRotateWithRight(K3->Left);return SingleRotateWithLeft(K3);
}static AvlTree DoubleRotateWithRight(AvlTree K1){ //RLK1->Right = SingleRotateWithLeft(K1->Right);return SingleRotateWithRight(K1);
}static AvlTree doBalance(AvlTree T){if(T == NULL)return NULL;resetHeight(T);int BF = caculatelBF(T);if(BF > 1){if(caculatelBF(T->Left) > 0)T = SingleRotateWithLeft(T);  // LLelseT = DoubleRotateWithLeft(T);  // LR} if(BF < -1){if(caculatelBF(T->Right) < 0)T = SingleRotateWithRight(T); // RRelseT = DoubleRotateWithRight(T); // RL}return T;
}AvlTree Insert(ElementType X, AvlTree T){if(T == NULL){T = malloc(sizeof(struct AvlNode));if(T == NULL){printf("Create AVL Tree ERROR\n");exit(0);}T->Element = X;T->Height = 0;T->Left = T->Right = NULL;} else if(X < T->Element){T->Left = Insert(X, T->Left);	} else if(X > T->Element){T->Right = Insert(X, T->Right);		}return doBalance(T);
}AvlTree Delete(ElementType X, AvlTree T){if(T == NULL){printf("Tree is null, delete fail\n");return NULL;}if(X < T->Element){T->Left = Delete(X, T->Left);} else if(X > T->Element){T->Right = Delete(X, T->Right);} else {AvlTree TmpCell;if(T->Left && T->Right){TmpCell = FindMin(T->Right);T->Element = TmpCell->Element;T->Right = Delete(T->Element, T->Right);} else {TmpCell = T;if(T->Left == NULL){T = T->Right;} else if(T->Right == NULL){T = T->Left;}free(TmpCell);}}return doBalance(T);
}

（3）测试代码如下，测试结果就不再展示了

#include <stdio.h>
#include <stdlib.h>
#include "AvlTree.h"int main(int argc, char *argv[]) {AvlTree T;AvlTree P;int i;int j = 0;T = MakeEmpty(NULL);for(i = 0; i < 50; i++, j = (j + 7) % 50 ){T = Insert(j, T);printf("after insert %d ==> root is %d, Height is %d || ", j, T->Element, T->Height);if(T->Left != NULL)printf("Tl = %d  ", T->Left->Element);elseprintf("Tl = NULL  ");if(T->Right != NULL)printf("Tr = %d  ", T->Right->Element);elseprintf("Tr = NULL");printf("\n");}for(i = 0; i < 50; i++)if((P = Find(i, T)) == NULL || Retrieve(P) != i)printf("Error at %d\n", i);printf("Min is %d, Max is %d\n", Retrieve(FindMin(T)), Retrieve(FindMax(T)));printf("Height is %d \n", T->Height);printf("\n\n\n===================================================\n\n");for(i = 1; i < 50; i += 2){T = Delete(i,T);printf("after delete %d ==> root is %d, Height is %d || ", i, T->Element, T->Height);if(T->Left != NULL)printf("Tl = %d  ", T->Left->Element);elseprintf("Tl = NULL  ");if(T->Right != NULL)printf("Tr = %d  ", T->Right->Element);elseprintf("Tr = NULL");printf("\n");}for(i = 0; i < 50; i += 2)if((P = Find( i, T )) == NULL || Retrieve(P) != i )printf( "Error at %d\n", i);for(i = 1; i < 50; i += 2)if((P = Find(i, T)) != NULL)printf("Error at %d\n", i);printf("Min is %d, Max is %d\n", Retrieve(FindMin(T)), Retrieve(FindMax(T)));printf("Height is %d \n", T->Height);return 0;
}

5-9 一些数学讨论

（1）推导：高度为h的AVL树的最少节点数$S(h)$的递推式

从AVL树的构型出发，很容易得到高度为h的AVL树，与其左右两边字数在节点函数$S(h)$的关系为：

$S(h)=S(h-1)+S(h-2)+1$

这个关系怎来的呢？考虑一般情况的AVL树：
1）AVL整棵树的平衡因子假设为1，那么左子树高度比右子树高度多1；
2）而整棵树的高度为h，除去根节点，那么左子树只能是h-1，右子树为h-2,；
3）综合以上两项，总结点数 = 左子树节点数 + 右子树节点数 + 1，此处的1就是根节点自己。

而节点数用函数$S(h)$表达，则明显有以上递推关系。

同理，在平衡因子为-1时，也存在相同的递推式；若平衡因子为0，则左右子树都是h-1，退化成$S(h)=2S(h-1)+1$。

（2）能否得到$S(h)$的具体解析式呢？

当然可以，零$T(h)=S(h)+1$，将上式两边同时加1，整理可得：$T(h)=T(h-1)+T(h-2)$，这不就是斐波那契数列吗？

在《黑皮书》第1/2两章的参考文献中，已经给出方法推导斐波那契数列的通项式（高中数学竞赛小姥们已经学过），这里我们就再推导一遍，需要准备的母函数（也叫生成函数，Generating Function）等数学知识（见[12],[13],[14]）。

定义成函数 $G(z)={\sum }_{n=0}^{\infty }{F}_n{z}^n$，$F_n$为斐波那契数列的第$n$项，$F_0=0$，$F_1=1$。
考虑到递推关系 $F_n=F_{n-1}+F_{n-2}$，可以尝试使用如下3个式子做变换：
$$\begin{array}{r}G(z)=F_0+F_{1}z+F_2{z}^2+F_3{z}^3+F_4{z}^4+F_5{z}^5+...\end{array}$$
$$\begin{array}{r}zG(z)=F_{0}z+F_1{z}^1+F_2{z}^3+F_3{z}^4+F_4{z}^5+F_5{z}^6+...\end{array}$$
$$\begin{array}{r}{z}^{2}G(z)=F_0{z}^2+F_1{z}^3+F_2{z}^4+F_3{z}^5+F_4{z}^6+F_5{z}^7+...\end{array}$$
易有
$$\begin{array}{r}(1-z-z^2)G(z)=F_0+(F_1-F_0)z+(F_2-F_1-F_0)z^2+(F_3-F_2-F_1)z^3+(F_4-F_3-F_2)z^4+...\end{array}$$
带入条件，等式右端仅留下$z$系数项，则
$$\begin{array}{r}G(z)=z/(1-z-z^2)\end{array}$$
求解方程 $1-z-z^2=0$，得到两根：$\varphi =\frac{1}{2}(1+\sqrt{5})$ ，$\hat{\varphi }=\frac{1}{2}(1-\sqrt{5})$，带入$G(z)$拆解分式
$$\begin{array}{r}G(z)=\frac{1}{\sqrt{5}}(\frac{1}{1-\varphi z}-\frac{1}{1-\hat{\varphi }z})\end{array}$$
利用等比数列级数展开式
$$\begin{array}{r}\frac{1}{1-z}=1+z+z^2+z^3+z^4+....\end{array}$$
$$\begin{array}{r}G(z)=\frac{1}{\sqrt{5}}(1+\varphi z+{\varphi }^2{z}^2+...-1-\hat{\varphi }z-\widehat{{\varphi }^2}{z}^2-...)\end{array}$$
对比系数有
$$\begin{array}{r}{F}_n=\frac{1}{\sqrt{5}}({\varphi }^n-\widehat{{\varphi }^n})\end{array}$$
那么
$$\begin{array}{r}S(h)=F_h-1=\frac{1}{\sqrt{5}}({\varphi }^n-\widehat{{\varphi }^n})-1\end{array}$$

（3）接下来参考文献 [6] 、[7]可得到树高$h$的渐进关系，其实也代表了AVL的查询深度
$$\begin{array}{r}h=O(logN)\end{array}$$
这与BST的结论一致，其实AVL就是一种BST，此处我们演示了另一种思路而已。

参考文献

[1] （北大）“数据结构与算法”教学大纲
[2] 平衡二叉树 —— 如何优雅的进行旋转（我和中意的一个有意思的博主，哈哈哈哈）
[3] 数据结构与算法分析学习笔记(二)–AVL树的算法思路整理
[4] 彻底搞懂AVL树
[5] 一文搞懂AVL树详解
[6] AVL tree 高度上下界推导
[7] AVL树的树高上下界极清晰推导
【注】相比之前BST的推导，这是很简单的啦
[8] 《算法4》
[9] 《黑皮书》
[10] 《计算机程序设计艺术》
[11] 清华大学，邓俊辉老师《数据结构》==> 这个讲的真的挺好的，点到为止，留足空间自学，但总能点中问题关键。
[12] 母函数——生成函数——形式级数
[13] 组合数学3 母函数
[14] 浅讲母函数