转自up：Naruto_Qcsdn：三维空间几何变换矩阵

先贴个站里分享的基础概念。

learn form 肥猫同学VFX b站：会用transform就会用矩阵

移动 旋转 缩放

1.transofrm ——输出变化矩阵

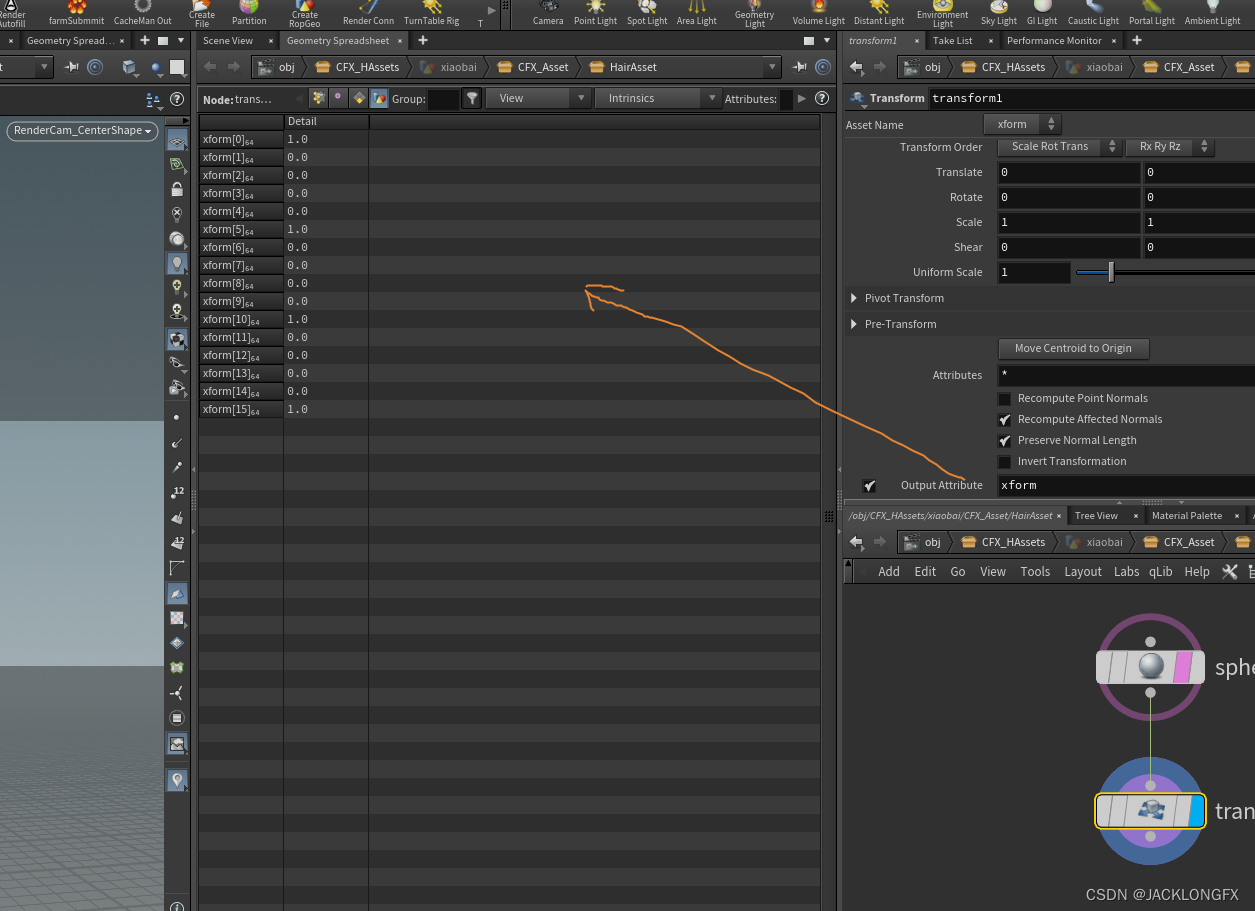
可以移动transform查看变化去理解

位移

缩放

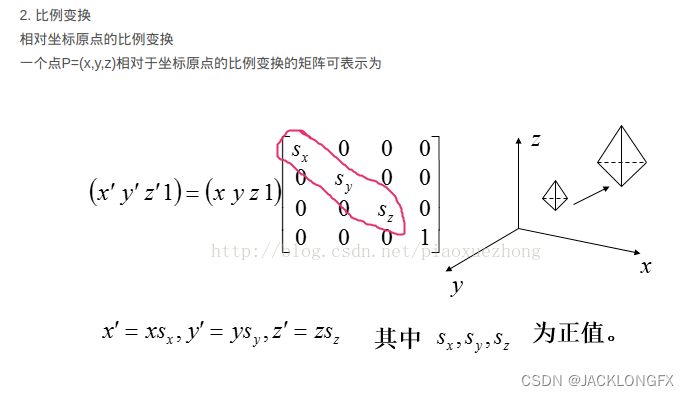
旋转

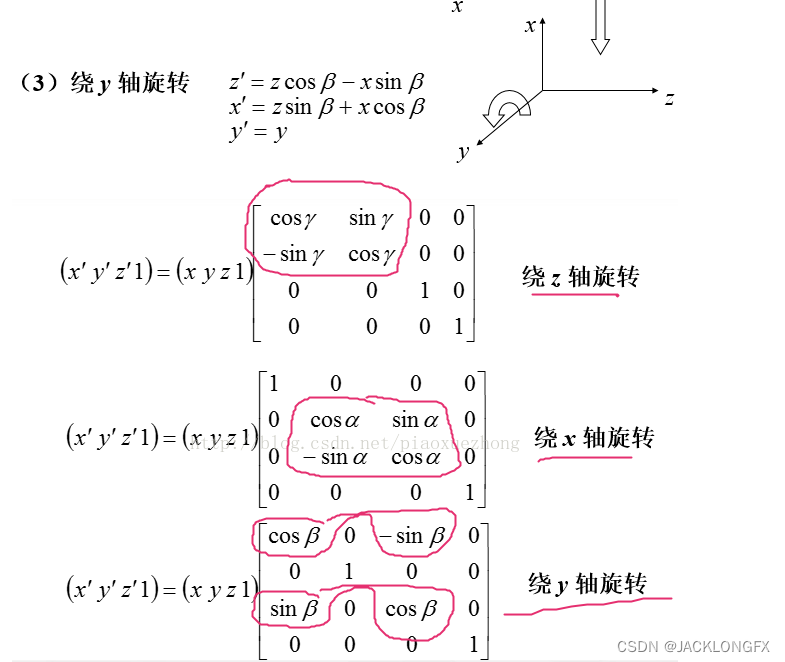
由此——3*3矩阵无法实现 ，位移

vex

4@m=ident（); //ch4('m')//单位矩阵
scale(@m,ch('sacle'));//缩放 对空间缩放（物体在空间内——同步缩放）float angle=radians(chf('angle'));
vector axis=chv('axis');
rotate(@m,angle,axis);// 旋转translate(@m,chv('tran'));//位移  or这里用3*3矩阵  最后@P+位移 也可以@P*=m；

lookat函数

vector p1=getbbox_center(0);
vector p2=point(1,'P',0);
martix3 m=lookat(p2,p1);
@P*=m;

dihedral 函数 让a转向b

绕指定轴转

vector a={0,1,0};
vector b=normlize(b向量);
martix3 m =dihedral(a,b);float angle=radians(chf('angle'));
rotate(@m,angle,b);// 旋转
@P*=m；

读取位移信息

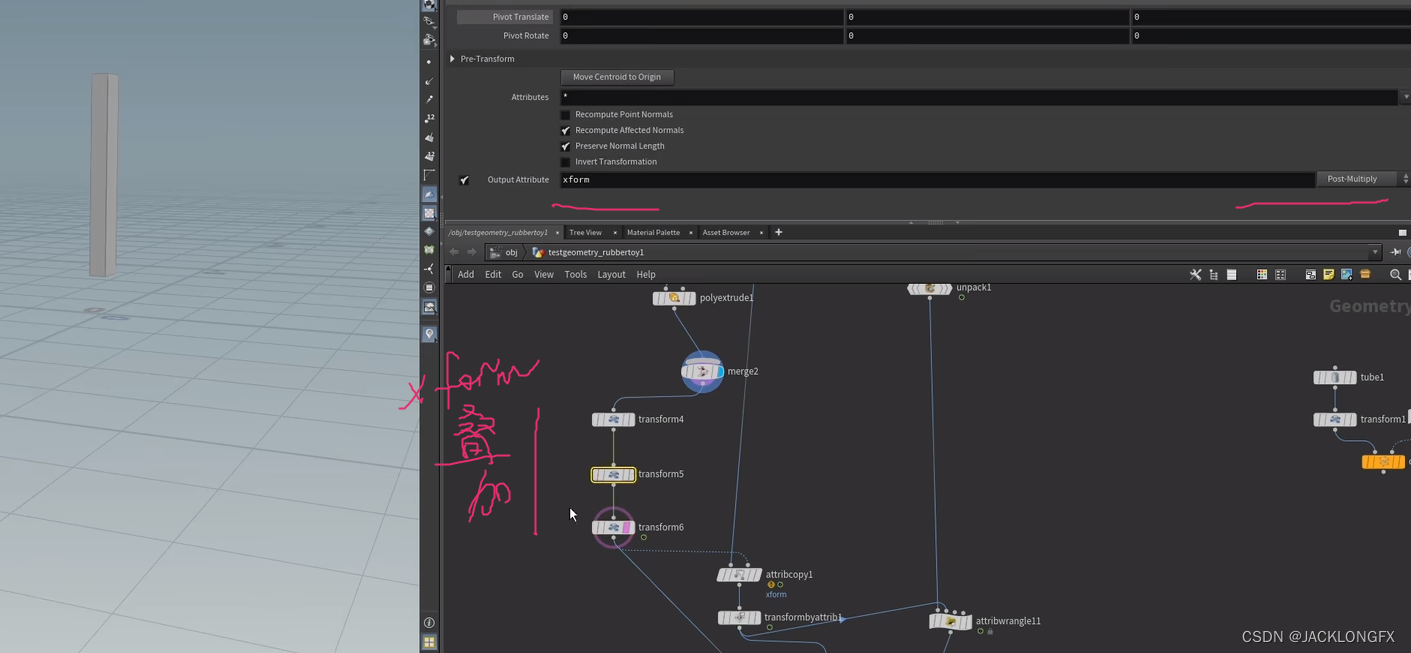
copy给物体

读取运动 这里等于复制了3个transform

maketransform

z +y+中心 定义4*4

vector zaxis=z;
vector yaxis=y;
vector translate=getbbox_center(1);
matrix m=maketransform(zaxis,yaxis,translate);
@P*=m;

3*3-------四元数

3@m=ident();
p@q=quaternion(3@m);

逆矩阵 invert
转置矩阵 transpose （eg:（m,n)矩阵A的行和列 给出的转置矩阵At 大小为（n,m））