题目:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
- 向右 -> 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1
思路:
这道题相对于力扣:62. 不同路径(动态规划,附python二维数组的定义)就是有了障碍。
不同路径中我们已经详细分析了没有障碍的情况,有障碍的话,其实就是标记对应的dp数组保持初始值0就可以了。
动规五部曲:
- 确定dp数组以及下标的含义(跟上题一样)
这里要明确dp数组的含义,定义dp数组是为了找到不同路径,
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
递归公式跟上题一样,dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点,因为有了障碍,(i, j)如果就是障碍的话应该就保持初始状态(初始状态为0)。
代码如下:
if obstacleGrid[i][j] == 0:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
- dp数组如何初始化
这里的初始化是重点,
如果(i, 0) 这条边有了障碍之后,障碍之后(包括障碍)都是走不到的位置了,所以障碍之后的dp[i][0]应该还是初始值0。下标(0, j)的初始化情况同理。
所以本题初始化代码为:
for i in range(n):if obstacleGrid[0][i] == 0:dp[0][i] = 1else:breakfor j in range(m):if obstacleGrid[j][0] == 0:dp[j][0] = 1else:break
注意:一旦遇到obstacleGrid[i][0] == 1的情况,一定要退出循环!不然之后障碍之后的点依旧会被赋值。
- 确定遍历顺序(跟上题一样)
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出,一定是从左到右一层一层遍历,这样保证推导dp[i][j]的时候,dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。
- 举例推导dp数组
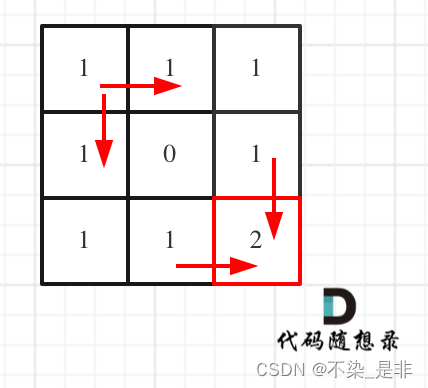
拿示例1来举例如题:

对应的dp数组如图:
完整代码:
class Solution:def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:# 获取网格的列数和行数n = len(obstacleGrid[0])m = len(obstacleGrid)# 如果起点或终点有障碍物,直接返回0if obstacleGrid[0][0] == 1 or obstacleGrid[m - 1][n - 1] == 1:return 0# 初始化一个二维数组dp,用于存储到达每个位置的路径数量dp = [[0] * n for _ in range(m)]# 初始化第一行,如果没有障碍物,则到达每个位置的路径数量为1,否则后面的位置均不可达for i in range(n):if obstacleGrid[0][i] == 0:dp[0][i] = 1else:break# 初始化第一列,如果没有障碍物,则到达每个位置的路径数量为1,否则后面的位置均不可达for j in range(m):if obstacleGrid[j][0] == 0:dp[j][0] = 1else:break# 计算其余位置的路径数量for i in range(1, m):for j in range(1, n):# 如果当前位置没有障碍物,则到达当前位置的路径数量为到达上方和左方位置的路径数量之和if obstacleGrid[i][j] == 0:dp[i][j] = dp[i - 1][j] + dp[i][j - 1]# 返回到达终点的路径数量return dp[m - 1][n - 1]复杂度分析:
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(n × m)

)











 详细讲解动态规划的思路)



(第40~42集))

