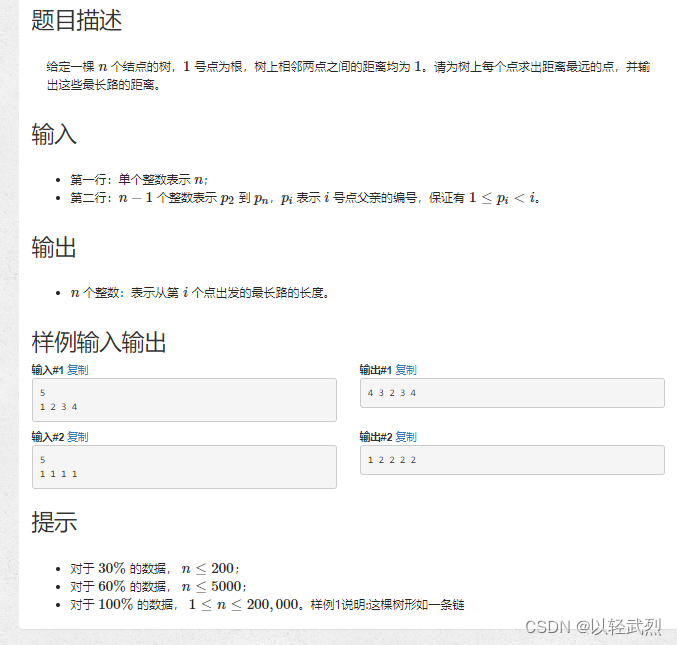
思路：树的最长路问题可以通过两次 DFS 求解，具体思路如下：

1.第一次 DFS 求树的直径
以任意一个点为起点进行深度优先遍历（DFS），找到与该点距离最远的点 u 。
以 u 为起点进行 DFS ，找到与 u 距离最远的点 v 。
则从 u 到 v 的路径即为树的直径。

2.第二次 DFS 求每个结点的最远距离
从树的中心节点（即直径的中间节点）出发，分别给两侧 DFS ，对于经过的每个结点，记录其到直径长度的最大值。

#include <bits/stdc++.h>
using namespace std;
const int maxn=2e5+50;
int n,ans[maxn],dp[maxn][3],fa[maxn],son[maxn];
vector<int> G[maxn];
void dfs1(int x)
{dp[x][0]=dp[x][1]=dp[x][2]=-1e9;//初始化为负无穷 dp[x][0]=0;//直接更新就好 for (int i=0;i<G[x].size();i++){int y=G[x][i];if (y==fa[x]) continue;fa[y]=x;dfs1(y);//处理儿子结点 int v=dp[y][0]+1;//v即为根到y的距离加1 if (v>dp[x][0]){dp[x][2]=dp[x][1];dp[x][1]=dp[x][0];dp[x][0]=v;son[x]=y;//记录最长链的末端 }else if (v>dp[x][1]){dp[x][2]=dp[x][1];dp[x][1]=v;}else if (v>dp[x][2]) dp[x][2]=v;}
}
void dfs2(int x,int len)//len是x到它父亲的距离 
{ans[x]=max(len,dp[x][0]);//更新答案 for (int i=0;i<G[x].size();i++){int y=G[x][i];if (y==fa[x]) continue;dfs2(y,max(len+1,(y==son[x]?dp[x][1]:dp[x][0])+1));//注意如果y是最长链末端的儿子，那么距离需要用次长链 }
}
int main()
{scanf("%d",&n);for (int i=2;i<=n;i++){int x;scanf("%d",&x);G[i].push_back(x);G[x].push_back(i);}dfs1(1);dfs2(1,0);for (int i=1;i<=n;i++) printf("%d ",ans[i]);return 0;
}