拓扑排序 是将一个有向无环图中的每个节点按照依赖关系进行排序。比如图$G$存在边$<u,v>$ 代表$v$的依赖$u$, 那么在拓扑排序中，节点$u$一定在$v$的前面。

从另一个角度看，拓扑排序是一种图遍历，具有两个性质：

• 图$G$中的每个节点$v$在排序序列中仅出现一次。
• 节点$v$当且仅当其依赖的所有节点$u$被访问完成，才被访问。

拓扑排序能够在$O(V+E)$的线性时间内完成，分为两种算法-Kahn算法和深度优先搜索

拓扑排序实例

这个图有很多有效的拓扑排序，包括：

视觉从左到右，从上到下：

5, 7, 3, 11, 8, 2, 9, 10

最小编号的可用顶点优先：

3, 5, 7, 8, 11, 2, 9, 10

按入边邻居的字典顺序：

3, 5, 7, 8, 11, 2, 10, 9

最少边数优先：

5, 7, 3, 8, 11, 2, 10, 9

最大编号的可用顶点优先：

7, 5, 11, 3, 10, 8, 9, 2

尝试从上到下，从左到右：

5, 7, 11, 2, 3, 8, 9, 10

任意顺序：

3, 7, 8, 5, 11, 10, 2, 9

Kahn算法

L ← Empty list that will contain the sorted elements
S ← Set of all nodes with no incoming edgewhile S is not empty doremove a node n from Sadd n to Lfor each node m with an edge e from n to m doremove edge e from the graphif m has no other incoming edges theninsert m into Sif graph has edges thenreturn error   (graph has at least one cycle)
else return L   (a topologically sorted order)

这个算法的思想是：

• 首先，在非空的有向无环图中，找到一组没有入边的起始节点，并将它们插入一个集合 S。上节图中的3,5,7 都是起始节点。
• 从S取出一个节点$n$，追加到列表L
• 对于每个依赖节点$n$的节点$m$, 删除边$<n,m>$
• 如果节点$m$变成起始节点，即入度为0， 那么加入集合S.
• 最后如果图中还有未删除的边，那说明图存在环路，无法拓扑排序；否则输出拓扑排序序列

算法依据的原理是什么？

无环图的正常遍历情况是这样的：

黄色代表集合S中的节点

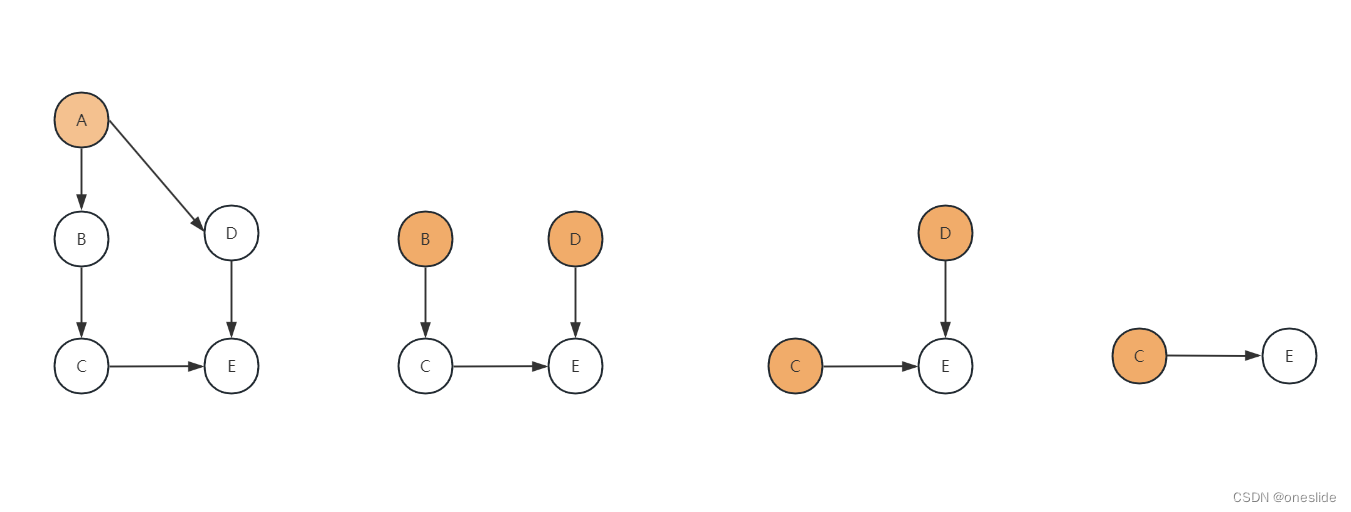
有环图的情况：

如果图G中有环，遍历至环路中任一节点，因为无法在环路中，找到任何一个开始节点进入环路，导致S为空，算法中止。

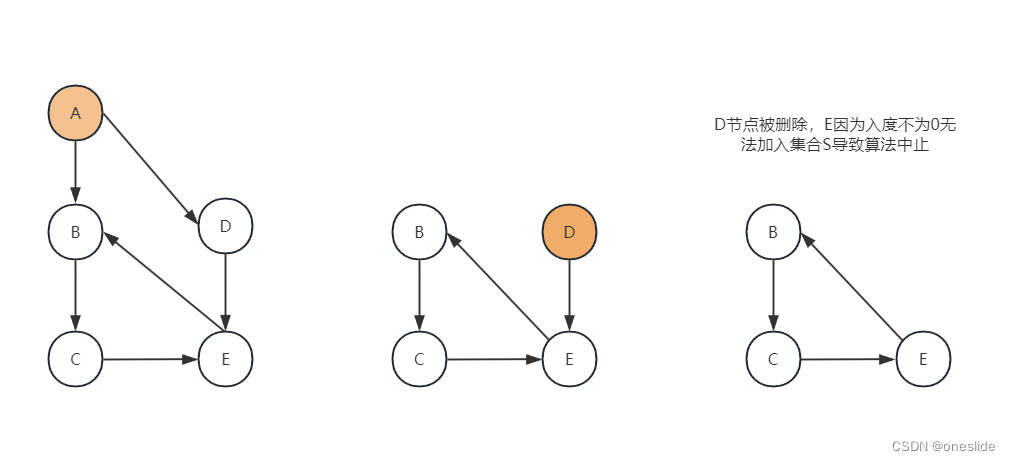
深度优先搜索

L ← Empty list that will contain the sorted nodes
while exists nodes without a permanent mark doselect an unmarked node nvisit(n)function visit(node n)if n has a permanent mark thenreturnif n has a temporary mark thenstop   (graph has at least one cycle)mark n with a temporary markfor each node m with an edge from n to m dovisit(m)remove temporary mark from nmark n with a permanent markadd n to head of L

Kahn算法会破坏原来图的数据，而深度优先不会。深度优先算法采取的是标记方式探测环路。

注意到节点$n$, 是添加到列表头部，因为是深度优先搜索，节点$n$带永久标记代表从$n$出发的能访问到的节点都被访问了,
即所有依赖节点$n$的节点都已在列表里了。

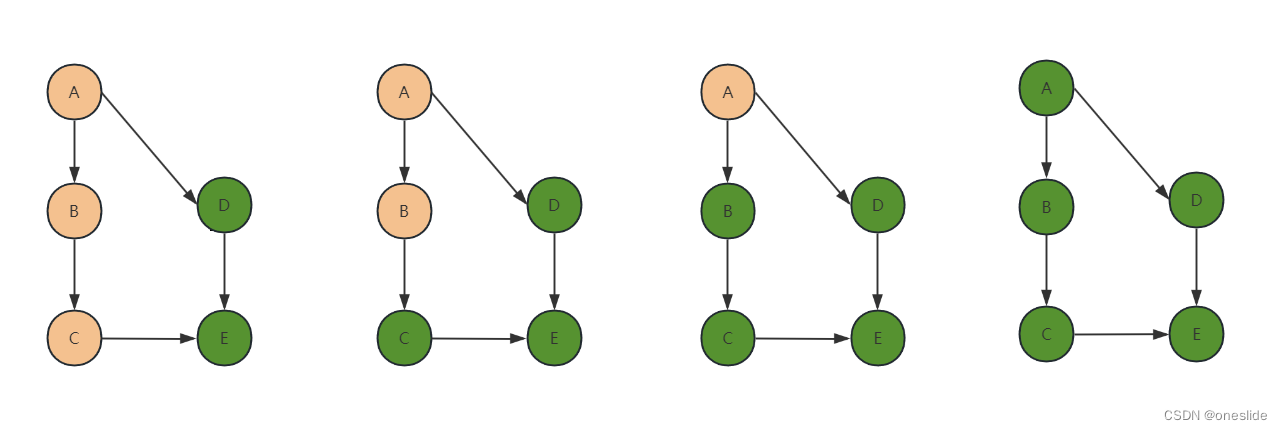
无环路情况

• 绿色为永久标记，代表从此节点出发的能访问到的节点都被访问了
• 橙色为临时标记

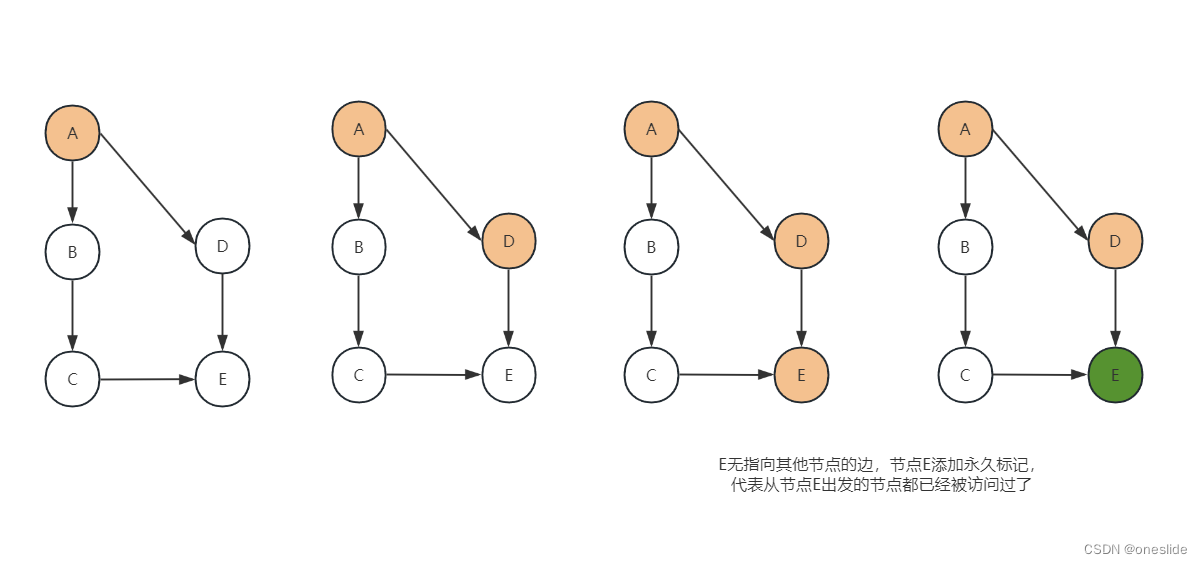
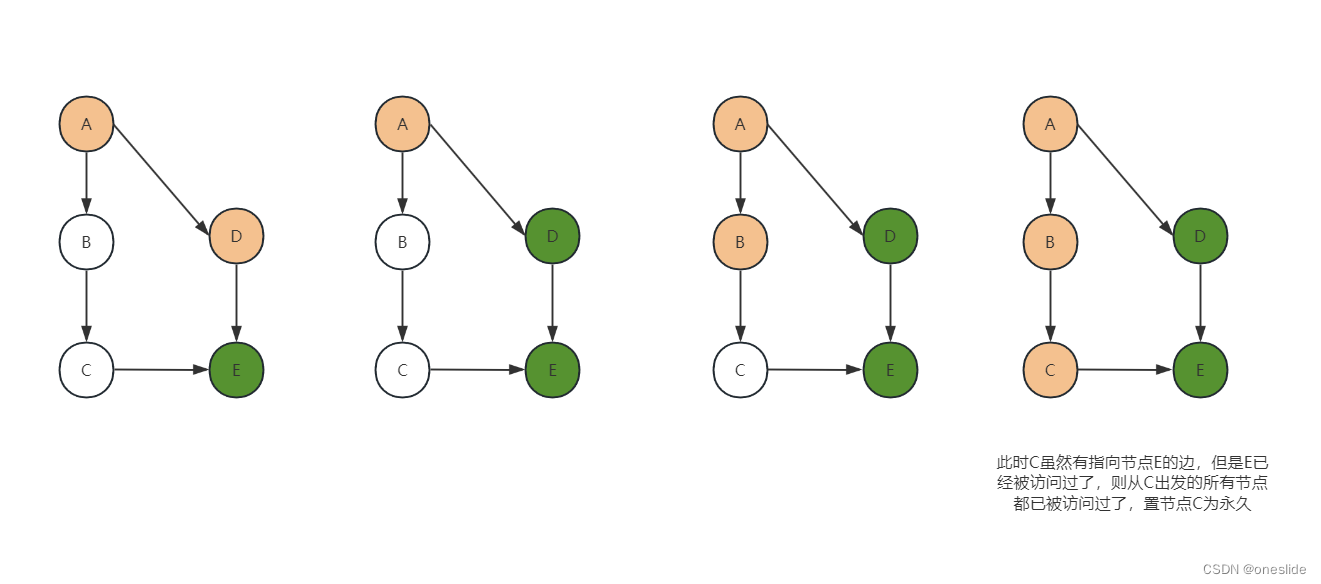
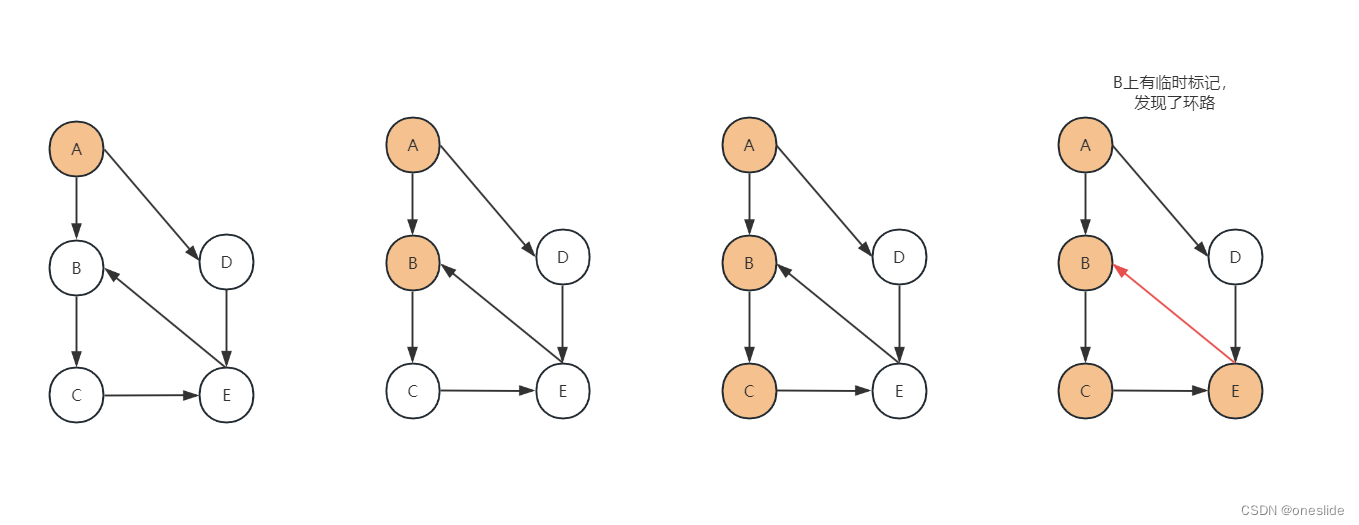
环路情况：