Description
二叉树用数组存储,将二叉树的结点数据依次自上而下,自左至右存储到数组中,一般二叉树与完全二叉树对比,比完全二叉树缺少的结点在数组中用0来表示。
计算二叉树每个结点的平衡因子,并按后序遍历的顺序输出结点的平衡因子。
–程序要求–
若使用C++只能include一个头文件iostream;若使用C语言只能include一个头文件stdio.h
程序中若include多过一个头文件,不看代码,作0分处理
不允许使用第三方对象或函数实现本题的要求
Input
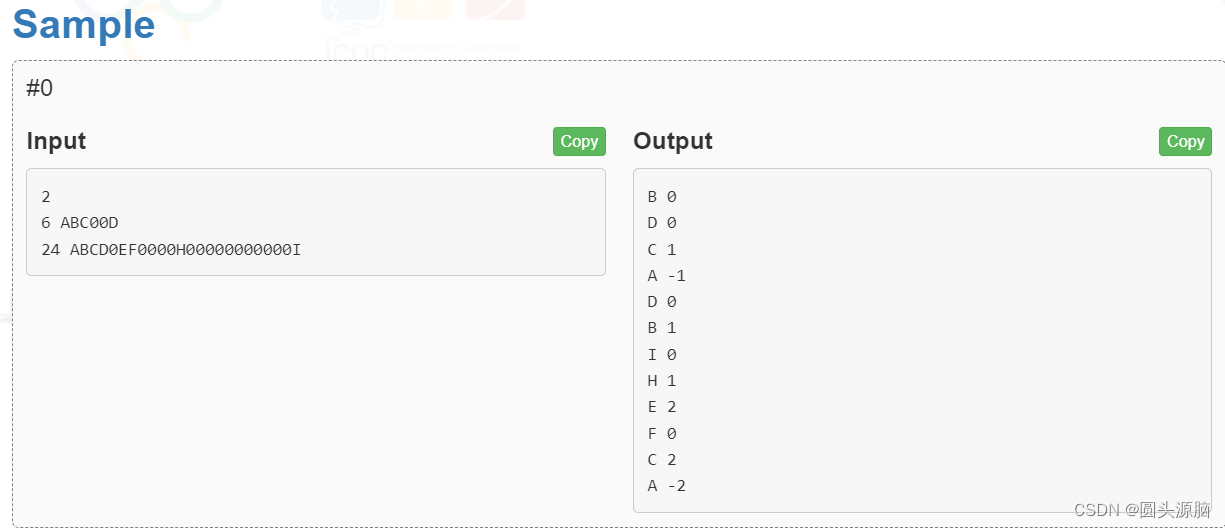
测试次数t
每组测试数据一行,数组元素个数n,后跟n个字符,二叉树的数组存储。
Output
对每组测试数据,按后序遍历的顺序输出树中结点的平衡因子(测试数据没有空树)
思路:
首先先要理解平衡因子的概念http://t.csdnimg.cn/RErze,推荐文章,有图文讲解很详细。
简单来说就是 平衡因子 = 左子树深度 - 右子树深度(当前节点)。
分配内存这里是把它补成满二叉树,然后就可以对数组直接进行操作


因为二叉树的结点数据依次自上而下,自左至右存储到数组中,可以在数组中直接操作
arr[0] 的左孩子是 arr[1*2 + 1] 右孩子是 arr[1*2 + 2];
arr[n] 的左孩子:arr[2*n + 1] 右孩子:arr[2*n + 2];

output函数进行递归并且输出结果。

主函数调用output();在类的public里面,传入参数0,数组的第0位,即二叉树的根节点。
左子树高度减去右子树高度即为输出结果。
AC代码:
#include <iostream>
using namespace std;// 二叉树类定义
class BinaryTree {
public:char* arr; // 数组用于存储二叉树节点int n; // 二叉树节点数int a; // 数组大小,以容纳二叉树节点// 构造函数,用于初始化具有给定节点数的二叉树BinaryTree(int numNodes) {allocateMemory(numNodes);}// 析构函数,释放动态分配的内存~BinaryTree() {delete[] arr;}// 初始化二叉树,将叶节点的值设置为 '0'void init() {for (int i = n; i < a; i++) {arr[i] = '0';}}// 输出二叉树结构和高度差void output() {output(0);}// 根据节点数分配二叉树数组的内存void allocateMemory(int numNodes) {n = numNodes;a = 2;while (a / 2 < n) {a *= 2;}arr = new char[a + 3];}// 计算指定节点的高度int height(int node) {if (arr[node] == '0') return 0;return height(node * 2 + 1) > height(node * 2 + 2) ? height(node * 2 + 1) + 1 : height(node * 2 + 2) + 1;}// 递归输出二叉树结构和高度差void output(int node) {if (arr[node] == '0') return;output(node * 2 + 1);output(node * 2 + 2);cout << arr[node] << " " << height(node * 2 + 1) - height(node * 2 + 2) << endl;}
};int main() {int t;cin >> t;while (t--) {int n;cin >> n;BinaryTree p(n);for (int i = 0; i < n; i++) {cin >> p.arr[i];}p.init();p.output();}return 0;
}




)


)

)





)



SpringCloud Alibaba入门简介)