给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

• 有效的算符为 '+'、'-'、'*' 和 '/' 。
• 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
• 两个整数之间的除法总是 向零截断 。
• 表达式中不含除零运算。
• 输入是一个根据逆波兰表示法表示的算术表达式。
• 答案及所有中间计算结果可以用 32 位 整数表示。

示例 1：

输入：tokens = ["2","1","+","3","*"]
输出：9
解释：该算式转化为常见的中缀算术表达式为：((2 + 1) * 3) = 9

示例 2：

输入：tokens = ["4","13","5","/","+"]
输出：6
解释：该算式转化为常见的中缀算术表达式为：(4 + (13 / 5)) = 6

示例 3：

输入：tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出：22
解释：该算式转化为常见的中缀算术表达式为：((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22

思路：

在上一篇文章中1047删除字符串中的所有相邻重复项提到了 递归就是用栈来实现的。

所以栈与递归之间在某种程度上是可以转换的！ 这一点我们在后续讲解二叉树的时候，会更详细的讲解到。

那么来看一下本题，其实逆波兰表达式相当于是二叉树中的后序遍历。 大家可以把运算符作为中间节点，按照后序遍历的规则画出一个二叉树。

但我们没有必要从二叉树的角度去解决这个问题，只要知道逆波兰表达式是用后序遍历的方式把二叉树序列化了，就可以了。

在进一步看，本题中每一个子表达式要得出一个结果，然后拿这个结果再进行运算，那么这岂不就是一个相邻字符串消除的过程，和的对对碰游戏是不是就非常像了。

如动画所示： 

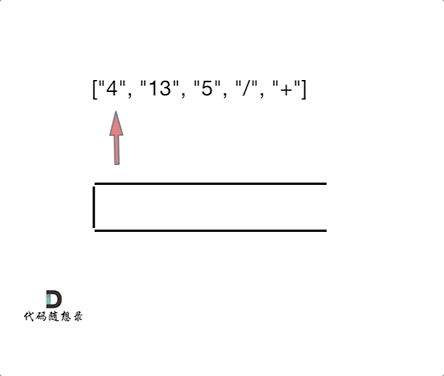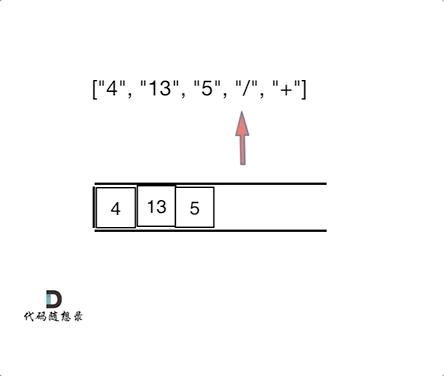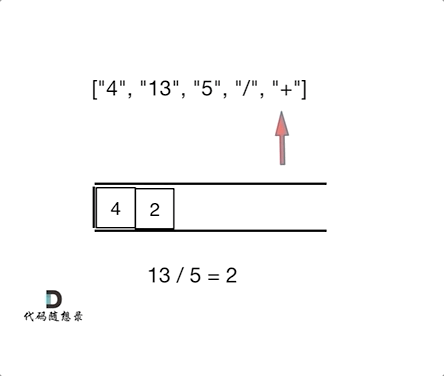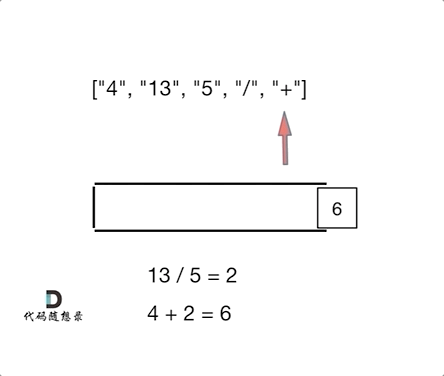
相信看完动画大家应该知道，这和1047. 删除字符串中的所有相邻重复项 (opens new window)是差不错的，只不过本题不要相邻元素做消除了，而是做运算！

C++代码如下：

class Solution {
public:int string_int(string s){if (s[0] >= '0' && s[0] <= '9'){int num = 0;for (int i = 0; i < s.size(); i++){num = num * 10 + (s[i] - '0');}return num;}else {int num = 0;for (int i = 1; i < s.size(); i++){num = num * 10 + (s[i] - '0');}return -num;}   }int evalRPN(vector<string>& tokens) {stack<int>sta;for (int i = 0; i < tokens.size(); i++){if (tokens[i] == "+"|| tokens[i] == "-"|| tokens[i] == "*"|| tokens[i] == "/"){int second = sta.top();sta.pop();int first = sta.top();sta.pop();if (tokens[i] == "+"){sta.push(first + second);}else if (tokens[i] == "-"){sta.push(first - second);}else if (tokens[i] == "*"){sta.push(first * second);}else if (tokens[i] == "/"){                  sta.push(first / second);}}else {sta.push(string_int(tokens[i]));}                                   }return sta.top();}
};