Leetcode 763 划分字母区间

题意理解：

        要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

        注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

        返回一个表示每个字符串片段的长度的列表。

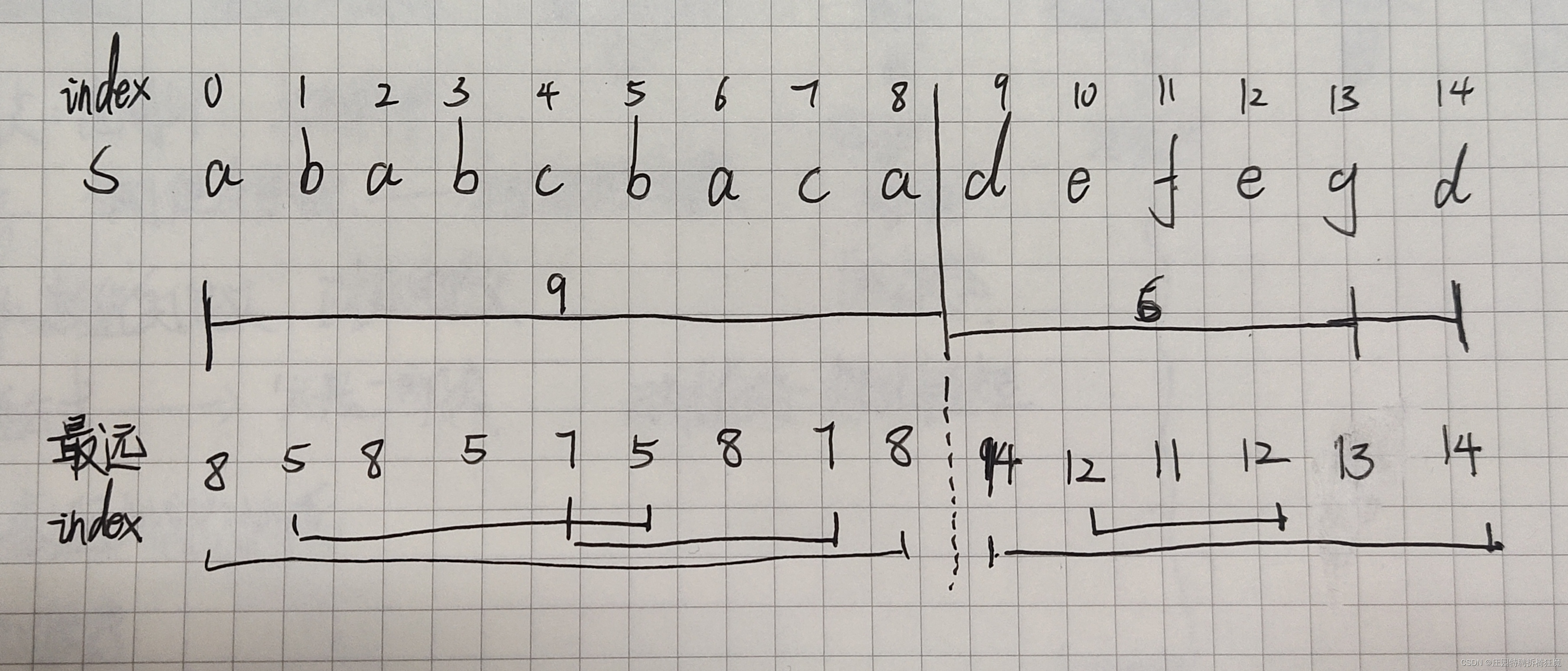
        输入：s = "ababc bacad efeg"
        输出：[9,6]

划分的结果是：当前片段内的字母不会出现在其他片段里

解题思路：

总是记录每个字母的最后出现的位置。则每个元素到其在s中出现的最后位置形成区间。

我们的目标是：同一个元素总是出现在一个片段里。

所以每个元素的出现区间总是包括在一个划分里。

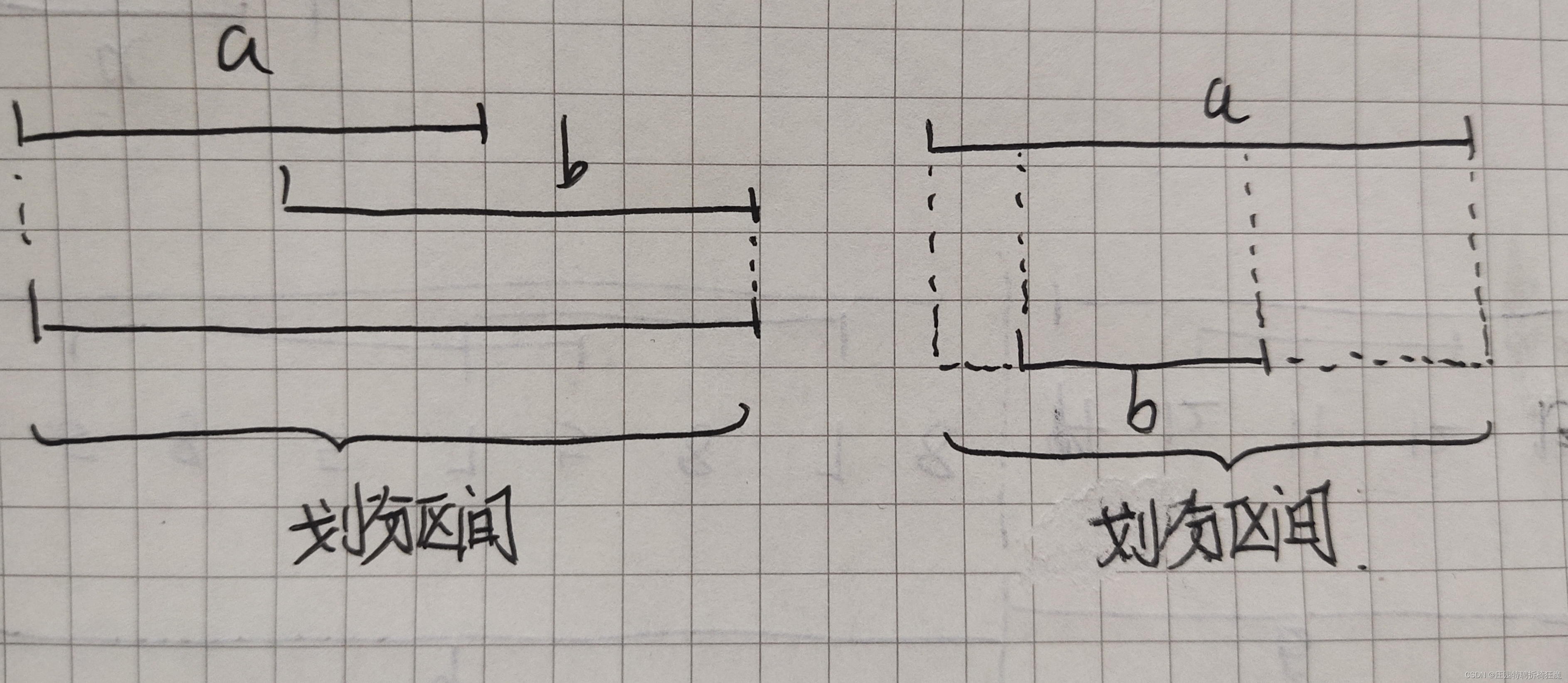
则该题就变成了一个区间重叠合并的问题。

如果两个元素的出现区间相互重叠，则须对区间的右区间进行延长，划分为一个区间片段。

我们采用贪心算法来解决这个问题，我们总是在区间的右边界上做延长，直到延长到最大可延长的位置，则划分为一个区间。

1.贪心解题

为了将其转换为区间合并问题，则：

首先记录每个元素的最后出现位置，与当前位置形成字母出现区间。

其次，根据出现区间实现区间右边界贪心探索。

直到右边界不能继续向右探索位置，可划分一个区间，区间数+1。

public List<Integer> partitionLabels(String s) {List<Integer> result=new ArrayList<>();//记录元素出现的最后一个位置int[] lastPoisition=new int[26];for(int i=0;i<s.length();i++){lastPoisition[s.charAt(i)-'a']=i;}//区间合并int left=0,right=lastPoisition[s.charAt(0)-'a'];for(int i=0;i<s.length();i++){//贪心右边界探索right=Math.max(right,lastPoisition[s.charAt(i)-'a']);//记录区间大小if(right==i){result.add(right-left+1);left=i+1;}}return result;}