线性支持向量机
- 线性支持向量机
- 间隔距离
- 学习的对偶算法
- 算法:线性可分支持向量机学习算法
- 线性可分支持向量机例子
谨以此博客作为复习期间的记录
线性支持向量机
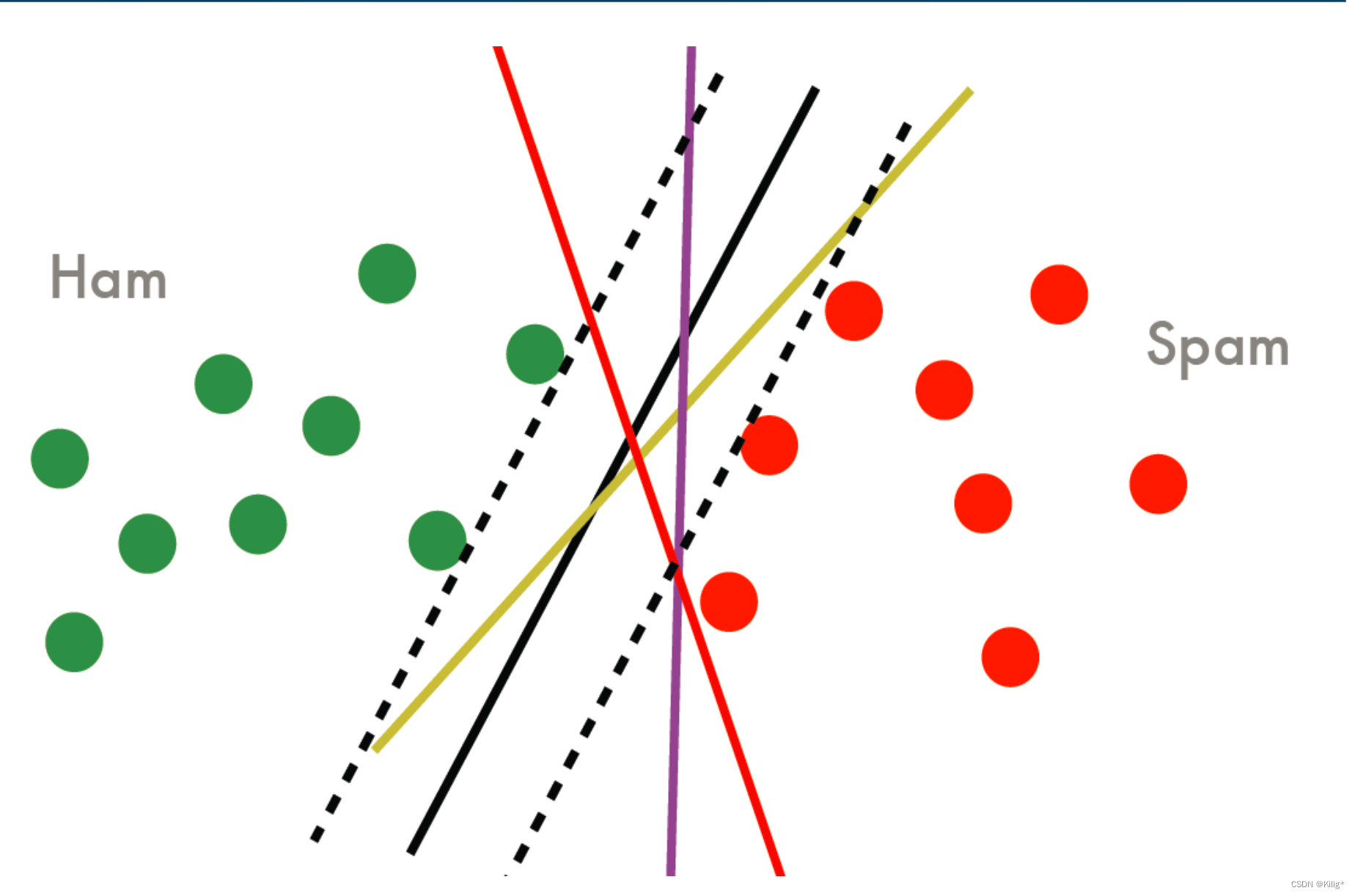
在以上四条线中,都可以作为分割平面,误差率也都为0。但是那个分割平面效果更好呢?其实可以看出,黑色的线具有更好的性质,因为如果将黑色的线作为分割平面,将会有更大的间隔距离。
其中,分割平面可以用以下式子表示:
w x + b = 0 wx+b = 0 wx+b=0
w 和 b w\text{和}b w和b都是有待学习的参数,SVM的核心思想之一就是找到这样的一个平面,使得间隔距离最大。那么该如何表述间隔距离呢?
间隔距离
在分割平面 w x + b = 0 wx+b = 0 wx+b=0确定的情况下,对每一个样本点 x i , ∣ w x i + b ∣ x_i,|wx_i+b| xi,∣wxi+b∣可以表示样本点 x i x_i xi到分割平面的距离。而若是二分类, y i ∈ { 1 , − 1 } y_i \in \{1,-1\} yi∈{1,−1},那么 y i ( w x i + b ) y_i(wx_i+b) yi(wxi+b)同样可以表示样本点到分割平面的距离。
对于二分类问题,数据点 x i \mathbf{x}_i xi 到超平面的函数间隔定义为: γ ^ i = y i ( w ⋅ x i + b ) \hat{\gamma}_i = y_i (\mathbf{w} \cdot \mathbf{x}_i + b) γ^i=yi(w⋅xi+b)
函数间隔的正负号表示数据点所属的类别和超平面分割的一致性。当 γ ^ i > 0 \hat{\gamma}_i > 0 γ^i>0 时,数据点 x i \mathbf{x}_i xi 被正确地分类到超平面两侧的区域,而当 γ ^ i < 0 \hat{\gamma}_i < 0 γ^i<0 时,数据点被错误地分类或位于超平面上。若 γ ^ i = 0 \hat{\gamma}_i = 0 γ^i=0,则表示数据点在超平面上。
而这里就可以得出SVM的初步思想:最大化最小函数间隔,公式表述如下
m a x m i n ( γ ^ i ) i = 1... N max \quad min(\hat{\gamma}_i) \qquad i = 1...N maxmin(γ^i)i=1...N
也就是在所有样本点 ( x i , y i ) (x_i,y_i) (xi,yi)中,可以找到离分割平面最近的点,我们想让这些点的距离达到最大。但是有一个问题,但是选择分离超平面时,只有函数间隔还不够.因为只要成比例地改变 w w w和 b b b ,例如将它们改为 2 w 2w 2w 和 2 b 2b 2b ,超平面并没有改变,但函数间隔却成为原来的 2 倍.这一事实启示我们,可以对分离超平面的法向量 w w w 加某些约束,如规范化 ∣ ∣ w ∣ ∣ = 1 ||w|| = 1 ∣∣w∣∣=1,这时函数间隔就变为了几何间隔。
几何间隔 对于给定的训练数据集 T T T 和超平面 ( w , b ) (w, b) (w,b), 定义超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 的几何间隔为
γ i = y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) \gamma_i=y_i\left(\frac{w}{\|w\|} \cdot x_i+\frac{b}{\|w\|}\right) γi=yi(∥w∥w⋅xi+∥w∥b)
定义超平面 ( w , b ) (w, b) (w,b) 关于训练数据集 T T T 的几何间隔为超平面 ( w , b ) (w, b) (w,b) 关于 T T T 中所有样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 的几何间隔之最小值, 即
γ = min i = 1 , ⋯ , N γ i \gamma=\min _{i=1, \cdots, N} \gamma_i γ=i=1,⋯,Nminγi
超平面 ( w , b ) (w, b) (w,b) 关于样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi) 的几何间隔一般是实例点到超平面的带符号的距离 (signed distance), 当样本点被超平面正确分类时就是实例点到超平面的距离.
从函数间隔和几何间隔的定义 (式(7.3) 式(7.6))可知, 函数间隔和几何间隔有下面的关系:
γ i = γ ^ i ∥ w ∥ γ = γ ^ ∥ w ∥ \begin{gathered} \gamma_i=\frac{\hat{\gamma}_i}{\|w\|} \\ \gamma=\frac{\hat{\gamma}}{\|w\|} \end{gathered} γi=∥w∥γ^iγ=∥w∥γ^
如果 ∥ w ∥ = 1 \|w\|=1 ∥w∥=1, 那么函数间隔和几何间隔相等. 如果超平面参数 w w w 和 b b b 成比例地改变 (超平面没有改变),函数间隔也按此比例改变,而几何间隔不变.
那么,优化目标可以等价的表述如下
maximize γ subject to γ ≤ y i ( w ∥ w ∥ ⋅ x i + b ∥ w ∥ ) , i = 1 , 2 , … , n \begin{align*} & \text{maximize} \quad \gamma \\ & \text{subject to} \quad \gamma \leq y_i \left(\frac{\mathbf{w}}{\|\mathbf{w}\|} \cdot \mathbf{x}_i + \frac{b}{\|\mathbf{w}\|}\right), \quad i = 1, 2, \dots, n \end{align*} maximizeγsubject toγ≤yi(∥w∥w⋅xi+∥w∥b),i=1,2,…,n
转化为几何间隔:
maximize γ ^ ∥ w ∥ subject to γ ^ ≤ y i ( w ⋅ x i + b ) , i = 1 , 2 , … , n \begin{align*} & \text{maximize} \quad \frac{\hat{\gamma}}{\|w\|} \\ & \text{subject to} \quad \hat{\gamma} \leq y_i \left(\mathbf{w} \cdot \mathbf{x}_i + b\right), \quad i = 1, 2, \dots, n \end{align*} maximize∥w∥γ^subject toγ^≤yi(w⋅xi+b),i=1,2,…,n
可以令 γ ^ = 1 \hat{\gamma} = 1 γ^=1,目标函数变为 m a x i m i z e 1 ∣ ∣ w ∣ ∣ maximize \quad\frac{1}{||w||} maximize∣∣w∣∣1,等价于 m i n i m i z e 1 2 ∣ ∣ w ∣ ∣ minimize\quad \frac{1}{2}||w|| minimize21∣∣w∣∣.原问题可化为以下形式.
minimize 1 2 ∣ ∣ w ∣ ∣ 2 subject to y i ( w ⋅ x i + b ) − 1 ≥ 0 , i = 1 , 2 , … , n \begin{align*} & \text{minimize} \quad \frac{1}{2}||w||^2\\ & \text{subject to} \quad y_i \left(\mathbf{w} \cdot \mathbf{x}_i + b\right) - 1\geq 0, \quad i = 1, 2, \dots, n \end{align*} minimize21∣∣w∣∣2subject toyi(w⋅xi+b)−1≥0,i=1,2,…,n
以上是一个凸优化问题,通过求解上述问题即可得到最终的最优决策平面。

在决定分离超平面时只有支持向量起作用,而其他实例点并不起作用.如果移动支持向量将改变所求的解;但是如果在间隔边界以外移动其他实例点,甚至去掉这些点,则解是不会改变的.由于支持向量在确定分离超平面中起着决定性作用,所以将这种分类模型称为支持向量机.支持向量的个数一般很少,所以支持向量机由很少的“重要的”训练样本确定.
学习的对偶算法
为了求解上述问题,可以构造拉格朗日函数,通过求解对偶问题得到原始问题的最优解。
这样做的优点,一是对偶问题往往更容易求解;二是自然引入核函数,进而推广到非线性分类问题。
首先构建拉格朗日函数 (Lagrange function). 为此, 对每一个不等式约束引进拉格朗日乘子 (Lagrange multiplier) α i ⩾ 0 , i = 1 , 2 , ⋯ , N \alpha_i \geqslant 0, i=1,2, \cdots, N αi⩾0,i=1,2,⋯,N, 定义拉格朗日函数:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|w\|^2-\sum_{i=1}^N \alpha_i y_i\left(w \cdot x_i+b\right)+\sum_{i=1}^N \alpha_i L(w,b,α)=21∥w∥2−i=1∑Nαiyi(w⋅xi+b)+i=1∑Nαi
其中, α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=\left(\alpha_1, \alpha_2, \cdots, \alpha_N\right)^{\mathrm{T}} α=(α1,α2,⋯,αN)T 为拉格朗日乘子向量.
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
max α min w , b L ( w , b , α ) \max _\alpha \min _{w, b} L(w, b, \alpha) αmaxw,bminL(w,b,α)
所以, 为了得到对偶问题的解, 需要先求 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 w , b w, b w,b 的极小, 再求对 α \alpha α 的极大.
拉格朗日函数为:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 N α i y i ( w ⋅ x i + b ) + ∑ i = 1 N α i L(w, b, \alpha)=\frac{1}{2}\|\mathbf{w}\|^2-\sum_{i=1}^N \alpha_i y_i(\mathbf{w} \cdot \mathbf{x}_i+b)+\sum_{i=1}^N \alpha_i L(w,b,α)=21∥w∥2−i=1∑Nαiyi(w⋅xi+b)+i=1∑Nαi
其中, α = ( α 1 , α 2 , ⋯ , α N ) T \alpha=\left(\alpha_1, \alpha_2, \cdots, \alpha_N\right)^{\mathrm{T}} α=(α1,α2,⋯,αN)T 为拉格朗日乘子向量。
接下来,我们进行极小化 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 w w w 和 b b b的过程。需要对 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 分别对 w w w 和 b b b 求偏导,并令其等于零:
对 w w w 的偏导数:
∂ L ∂ w = w − ∑ i = 1 N α i y i x i = 0 \frac{\partial L}{\partial w} = w - \sum_{i=1}^N \alpha_i y_i x_i = 0 ∂w∂L=w−∑i=1Nαiyixi=0
得到: w = ∑ i = 1 N α i y i x i w = \sum_{i=1}^N \alpha_i y_i x_i w=∑i=1Nαiyixi
对 b b b 的偏导数:
∂ L ∂ b = − ∑ i = 1 N α i y i = 0 \frac{\partial L}{\partial b} = -\sum_{i=1}^N \alpha_i y_i = 0 ∂b∂L=−∑i=1Nαiyi=0
得到: ∑ i = 1 N α i y i = 0 \sum_{i=1}^N \alpha_i y_i = 0 ∑i=1Nαiyi=0
将上述对 w w w 和 b b b 的结果代入拉格朗日函数 L ( w , b , α ) L(w, b, \alpha) L(w,b,α),得到极小化后的结果
这样,对偶问题可以表示为:
min α − 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) + ∑ i = 1 N α i \min_\alpha -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j (x_i \cdot x_j) + \sum_{i=1}^N \alpha_i αmin−21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)+i=1∑Nαi
其中, α i ⩾ 0 \alpha_i \geqslant 0 αi⩾0, i = 1 , 2 , ⋯ , N i=1, 2, \cdots, N i=1,2,⋯,N,并且满足 ∑ i = 1 N α i y i = 0 \sum_{i=1}^N \alpha_i y_i = 0 ∑i=1Nαiyi=0。
然后,对拉格朗日函数 L ( w , b , α ) L(w, b, \alpha) L(w,b,α) 对 α \alpha α 求极大值,这样就可以得到对偶问题的解。
那么求解得到 α \alpha α之后,该如何反求出 w ∗ , b ∗ w^*,b^* w∗,b∗呢?
根据KKT条件,有
∇ w L ( w ∗ , b ∗ , α ∗ ) = w ∗ − ∑ i = 1 N α i ∗ y i x i = 0 ∇ b L ( w ∗ , b ∗ , α ∗ ) = − ∑ i = 1 N α i ∗ y i = 0 α i ∗ ( y i ( w ∗ ⋅ x i + b ∗ ) − 1 ) = 0 , i = 1 , 2 , ⋯ , N y i ( w ∗ ⋅ x i + b ∗ ) − 1 ⩾ 0 , i = 1 , 2 , ⋯ , N α i ∗ ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} & \nabla_w L\left(w^*, b^*, \alpha^*\right)=w^*-\sum_{i=1}^N \alpha_i^* y_i x_i=0 \\ & \nabla_b L\left(w^*, b^*, \alpha^*\right)=-\sum_{i=1}^N \alpha_i^* y_i=0 \\ & \alpha_i^*\left(y_i\left(w^* \cdot x_i+b^*\right)-1\right)=0, \quad i=1,2, \cdots, N \\ & y_i\left(w^* \cdot x_i+b^*\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \\ & \alpha_i^* \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} ∇wL(w∗,b∗,α∗)=w∗−i=1∑Nαi∗yixi=0∇bL(w∗,b∗,α∗)=−i=1∑Nαi∗yi=0αi∗(yi(w∗⋅xi+b∗)−1)=0,i=1,2,⋯,Nyi(w∗⋅xi+b∗)−1⩾0,i=1,2,⋯,Nαi∗⩾0,i=1,2,⋯,N
由此得
w ∗ = ∑ i α i ∗ y i x i w^*=\sum_i \alpha_i^* y_i x_i w∗=i∑αi∗yixi
其中至少有一个 α j ∗ > 0 \alpha_j^*>0 αj∗>0 (用反证法, 假设 α ∗ = 0 \alpha^*=0 α∗=0, 由第一条KKT条件可知 w ∗ = 0 w^*=0 w∗=0, 而 w ∗ = 0 w^*=0 w∗=0不是原始最优化问题的解, 产生矛盾), 对此 j j j 有
y j ( w ∗ ⋅ x j + b ∗ ) − 1 = 0 y_j\left(w^* \cdot x_j+b^*\right)-1=0 yj(w∗⋅xj+b∗)−1=0
有 y j 2 = 1 y_j^2 = 1 yj2=1, y j ( w ∗ ⋅ x j + b ∗ ) − y j 2 = 0 y_j\left(w^* \cdot x_j+b^*\right)-y_j^2=0 yj(w∗⋅xj+b∗)−yj2=0进而得出 w ∗ ⋅ x j + b ∗ − y j = 0 w^* \cdot x_j+b^* - y_j = 0 w∗⋅xj+b∗−yj=0
因此,在求解出 α ∗ \alpha^* α∗之后,可以得到决策平面的 w ∗ 和 b ∗ w^*和b^* w∗和b∗
w ∗ = ∑ i α i ∗ y i x i b ∗ = y j − w ∗ ⋅ x j w^*=\sum_i \alpha_i^* y_i x_i\\ b^* = y_j - w^* \cdot x_j w∗=i∑αi∗yixib∗=yj−w∗⋅xj
算法:线性可分支持向量机学习算法
输入: 线性可分训练集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , ⋯ , ( x N , y N ) } T=\left\{\left(x_1, y_1\right),\left(x_2, y_2\right), \cdots,\left(x_N, y_N\right)\right\} T={(x1,y1),(x2,y2),⋯,(xN,yN)}, 其中 x i ∈ X = R n , y i ∈ x_i \in \mathcal{X}=\mathbf{R}^n, y_i \in xi∈X=Rn,yi∈ Y = { − 1 , + 1 } , i = 1 , 2 , ⋯ , N \mathcal{Y}=\{-1,+1\}, \quad i=1,2, \cdots, N Y={−1,+1},i=1,2,⋯,N;
输出: 分离超平面和分类决策函数.
(1)构造并求解约束最优化问题
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} & \min _\alpha \quad \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ & \text { s.t. } \quad \sum_{i=1}^N \alpha_i y_i=0 \\ & \alpha_i \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi s.t. i=1∑Nαiyi=0αi⩾0,i=1,2,⋯,N
求得最优解 α ∗ = ( α 1 ∗ , α 2 ∗ , ⋯ , α N ∗ ) T \alpha^*=\left(\alpha_1^*, \alpha_2^*, \cdots, \alpha_N^*\right)^{\mathrm{T}} α∗=(α1∗,α2∗,⋯,αN∗)T.
(2) 计算
w ∗ = ∑ i = 1 N α i ∗ y i x i w^*=\sum_{i=1}^N \alpha_i^* y_i x_i w∗=i=1∑Nαi∗yixi
并选择 α ∗ \alpha^* α∗ 的一个正分量 α j ∗ > 0 \alpha_j^*>0 αj∗>0, 计算
b ∗ = y j − ∑ i = 1 N α i ∗ y i ( x i ⋅ x j ) b^*=y_j-\sum_{i=1}^N \alpha_i^* y_i\left(x_i \cdot x_j\right) b∗=yj−i=1∑Nαi∗yi(xi⋅xj)
(3) 求得分离超平面
w ∗ ⋅ x + b ∗ = 0 w^* \cdot x+b^*=0 w∗⋅x+b∗=0
分类决策函数:
f ( x ) = sign ( w ∗ ⋅ x + b ∗ ) f(x)=\operatorname{sign}\left(w^* \cdot x+b^*\right) f(x)=sign(w∗⋅x+b∗)
在线性可分支持向量机中, w ∗ w^* w∗ 和 b ∗ b^* b∗ 只依赖于训练数据中对应于 α i ∗ > 0 \alpha_i^*>0 αi∗>0 的样本点 ( x i , y i ) \left(x_i, y_i\right) (xi,yi), 而其他样本点对 w ∗ w^* w∗ 和 b ∗ b^* b∗ 没有影响. 我们将训练数据中对应于 α i ∗ > 0 \alpha_i^*>0 αi∗>0 的实例点 x i ∈ R n x_i \in \mathbf{R}^n xi∈Rn 称为支持向量.
线性可分支持向量机例子

带入
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i s.t. ∑ i = 1 N α i y i = 0 α i ⩾ 0 , i = 1 , 2 , ⋯ , N \begin{aligned} & \min _\alpha \quad \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ & \text { s.t. } \quad \sum_{i=1}^N \alpha_i y_i=0 \\ & \alpha_i \geqslant 0, \quad i=1,2, \cdots, N \end{aligned} αmin21i=1∑Nj=1∑Nαiαjyiyj(xi⋅xj)−i=1∑Nαi s.t. i=1∑Nαiyi=0αi⩾0,i=1,2,⋯,N
解 根据所给数据, 对偶问题是
min α 1 2 ∑ i = 1 N ∑ j = 1 N α i α j y i y j ( x i ⋅ x j ) − ∑ i = 1 N α i = 1 2 ( 18 α 1 2 + 25 α 2 2 + 2 α 3 2 + 42 α 1 α 2 − 12 α 1 α 3 − 14 α 2 α 3 ) − α 1 − α 2 − α 3 s.t. α 1 + α 2 − α 3 = 0 α i ⩾ 0 , i = 1 , 2 , 3 \begin{array}{ll} \min _\alpha & \frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N \alpha_i \alpha_j y_i y_j\left(x_i \cdot x_j\right)-\sum_{i=1}^N \alpha_i \\ & =\frac{1}{2}\left(18 \alpha_1^2+25 \alpha_2^2+2 \alpha_3^2+42 \alpha_1 \alpha_2-12 \alpha_1 \alpha_3-14 \alpha_2 \alpha_3\right)-\alpha_1-\alpha_2-\alpha_3 \\ \text { s.t. } & \alpha_1+\alpha_2-\alpha_3=0 \\ & \alpha_i \geqslant 0, \quad i=1,2,3 \end{array} minα s.t. 21∑i=1N∑j=1Nαiαjyiyj(xi⋅xj)−∑i=1Nαi=21(18α12+25α22+2α32+42α1α2−12α1α3−14α2α3)−α1−α2−α3α1+α2−α3=0αi⩾0,i=1,2,3
解这一最优化问题. 将 α 3 = α 1 + α 2 \alpha_3=\alpha_1+\alpha_2 α3=α1+α2 代入目标函数并记为
s ( α 1 , α 2 ) = 4 α 1 2 + 13 2 α 2 2 + 10 α 1 α 2 − 2 α 1 − 2 α 2 s\left(\alpha_1, \alpha_2\right)=4 \alpha_1^2+\frac{13}{2} \alpha_2^2+10 \alpha_1 \alpha_2-2 \alpha_1-2 \alpha_2 s(α1,α2)=4α12+213α22+10α1α2−2α1−2α2
对 α 1 , α 2 \alpha_1, \alpha_2 α1,α2 求偏导数并令其为 0 , 易知 s ( α 1 , α 2 ) s\left(\alpha_1, \alpha_2\right) s(α1,α2) 在点 ( 3 2 , − 1 ) T \left(\frac{3}{2},-1\right)^{\mathrm{T}} (23,−1)T 取极值, 但该点不满足约束条件 α 2 ⩾ 0 \alpha_2 \geqslant 0 α2⩾0, 所以最小值应在边界上达到.
当 α 1 = 0 \alpha_1=0 α1=0 时, 最小值 s ( 0 , 2 13 ) = − 2 13 s\left(0, \frac{2}{13}\right)=-\frac{2}{13} s(0,132)=−132; 当 α 2 = 0 \alpha_2=0 α2=0 时, 最小值 s ( 1 4 , 0 ) = − 1 4 s\left(\frac{1}{4}, 0\right)=-\frac{1}{4} s(41,0)=−41. 于是 s ( α 1 , α 2 ) s\left(\alpha_1, \alpha_2\right) s(α1,α2) 在 α 1 = 1 4 , α 2 = 0 \alpha_1=\frac{1}{4}, \alpha_2=0 α1=41,α2=0 达到最小, 此时 α 3 = α 1 + α 2 = 1 4 \alpha_3=\alpha_1+\alpha_2=\frac{1}{4} α3=α1+α2=41.
这样, α 1 ∗ = α 3 ∗ = 1 4 \alpha_1^*=\alpha_3^*=\frac{1}{4} α1∗=α3∗=41 对应的实例点 x 1 , x 3 x_1, x_3 x1,x3 是支持向量. 计算得
w 1 ∗ = w 2 ∗ = 1 2 b ∗ = − 2 \begin{gathered} w_1^*=w_2^*=\frac{1}{2} \\ b^*=-2 \end{gathered} w1∗=w2∗=21b∗=−2
分离超平面为
1 2 x ( 1 ) + 1 2 x ( 2 ) − 2 = 0 \frac{1}{2} x^{(1)}+\frac{1}{2} x^{(2)}-2=0 21x(1)+21x(2)−2=0
分类决策函数为
f ( x ) = sign ( 1 2 x ( 1 ) + 1 2 x ( 2 ) − 2 ) f(x)=\operatorname{sign}\left(\frac{1}{2} x^{(1)}+\frac{1}{2} x^{(2)}-2\right) f(x)=sign(21x(1)+21x(2)−2)




结构体实现位段最终篇)

——特征编码)












