目录
1.排序
1.插入排序模板
2.冒泡排序模板
3.选择排序模板
2.搜索
1.顺序搜索
2.二分搜索
3.迭代
1.基础迭代
编辑
4.求最大公因数,最小公倍数
1.最直接的方法
取巧一点
2.辗转相除法(欧几里得法)
1.排序
1.插入排序模板
插入排序就如同一副扑克牌,我们一张一张的开始摸牌,一张一张的放,找到相应的位置,让后面的牌往后挪一格,再把这个牌放到挪往后的这个空位上
#include<stdio.h>
#include<math.h>
#include<string.h>int main(){for(int i = 1; i <= 6; i++) scanf("%d",&a[i]);//摸6张牌,从小到大排序for(int i = 1; i <= 6; i++){int temp = a[i];//摸牌for(int j = i; j > 0&&a[j-1] > temp; j--){//从第i张牌开始比较,只要前一张牌比它大并且没比较到第一张牌就换位置a[j] = a[j+1];//往后挪一格}a[i] = temp;//新牌落位}return 0;
}

2.冒泡排序模板
冒泡排序
冒泡排序其实我之前写过一个模板
http://t.csdnimg.cn/ghWXo
这次多加点注释,讲的更详细
冒泡排序其实它的名字就十分的形象,就把每个元素都看作是一个泡泡,每次都比较泡泡的大小,如果那个泡泡更大,就让它到前面去,这样一遍又一遍的比较下去,使得泡泡成功变为从小到大的排序
借助动图理解

#include<stdio.h>
#include<math.h>
#include<string.h>int main(){int a[7];for(int i = 1; i <= 6; i++) scanf("%d",&a[i]);//将6个元素,从小到大排序for(int i = 1; i <= 5; i++){int flag = 0;//6个元素只用冒泡5次,或者说n个元素,冒泡n-1次//对于最后一次冒泡的时候,它后面的元素都已经比较好了for(int j = 1; j <= 6-i; j++){//6个元素要冒泡6-冒泡的次数//举个例子,三个数,第一次冒泡,要比较两次//对第二次来说,却只要比较一次就可以了if(a[j] > a[j+1]){//如果这个数比它的下一个数大,就交换位置int t = a[j+1];a[j+1] = a[j];a[j] = t;flag = 1;//flag有优化的作用,如果在进行完这个if后//flag仍然为0,说明一次比较都没有进行,即说明此时已经排序好了}}if(flag == 0) break;}for(int i = 1; i <= 6; i++) printf("%d ",a[i]);return 0;
}
3.选择排序模板
选择排序是找一个数组中最大的那个数,把它放在第一个位置,再从剩下的数中找到最大的放在第二个位置,以此类推,直到只有两个数,把这两个数中更大的放在倒数第二个位置,另外一个放在最后
#include<stdio.h>
#include<math.h>
#include<string.h>int main(){int a[7];for(int i = 1; i <= 6; i++) scanf("%d",&a[i]);for(int i = 1; i <= 5; i++){int k = i;//记录下标for(int j = k+1; j <= 6; j++){if(a[j] < a[k]) k = j;}//此时k为值最大的那个数的下标if(k!=i) {int t = a[k]; a[k] = a[i]; a[i] = t;}}for(int i = 1; i <= 6; i++) printf("%d ",a[i]);return 0;
}
2.搜索
1.顺序搜索
顺序搜索就是写个循环从头搜索到尾,效率很低
2.二分搜索
二分搜索就是对一个已经排序好的数组,不断的二分找我们要找的那个数字
http://t.csdnimg.cn/J6kJd
这是我之前写过的一个二分模板,这次写个更加规范的
#include<stdio.h>
#include<math.h>
#include<string.h>int main(){int a[] = {1,2,3,4,5,6,7,8,9,10};int left = 0,right = 9,mid,found;//left为第一个数的下标,也就是0//right为第二个数的下标,也就是1//mid为二分的那个值//found用来判断是否找到了,找到则为1found = 0;int x;scanf("%d",&x);//要找xwhile(left <= right && !found){mid = (left + right)/2;if(a[mid] > x) right = mid - 1;else if(a[mid] < x) left = mid + 1;else if(a[mid] == x) found = 1;}if(found == 1) printf("found");else printf("nofound");return 0;
}

3.迭代
1.基础迭代
#include<stdio.h>
const int N = 1e5 + 10;int main(){int a[N];int n,i;scanf("%d",&n);a[1] = 1,printf("%5d",a[1]);a[2] = 1,printf("%5d",a[2]);for( i = 3; i <= n;i++){a[i] = a[i - 1] + a[i - 2];printf("%5d",a[i]);}return 0 ;
}4.求最大公因数,最小公倍数
最大公因数 的英文是 "Greatest Common Divisor"
最小公倍数 Least Common Multiple
以下用gcd代表最大公因数,用lcm代表最小公倍数
1.最直接的方法
让那两个数中更大的那个数一直加一,直到能被那两个数整除为止,得到的这个数就是最小公倍数
让那两个数中更小的那个数一直减一,直到那两个数能被这个数整除为止,得到的这个数就是最大公因数
#include<stdio.h>
#include<math.h>
#include<string.h>int lcm(int x,int y){int max = x>y?x:y;while(max%x != 0||max%y != 0) max++;//只要max不能同时被这两个数整除就加一return max;
}int gcd(int x,int y){int min = x < y?x:y;while(x % min != 0|| y % min != 0) min--;//直到那两个数能被这个数整除为止return min;
}
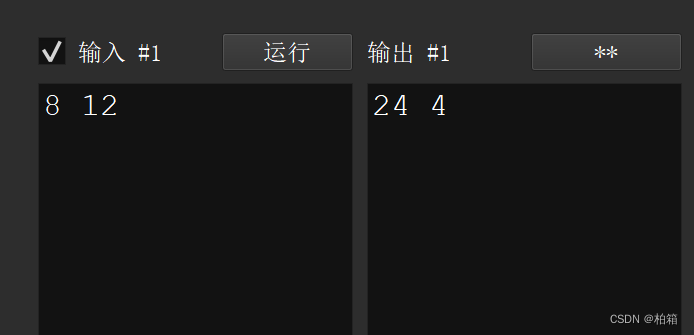
int main(){int x,y;scanf("%d%d",&x,&y);//找x和y的最小公倍数和最大公因数int lc,gc;lc = lcm(x,y);gc = gcd(x,y);printf("%d %d",lc,gc);return 0;
}
取巧一点
最小公倍数其实就是x乘y除以最大公因数
可以变成这样
#include<stdio.h>
#include<math.h>
#include<string.h>int gcd(int x,int y){int min = x < y?x:y;while(x % min != 0|| y % min != 0) min--;//直到那两个数能被这个数整除为止return min;
}int lcm(int x,int y){return x*y/gcd(x,y);
}int main(){int x,y;scanf("%d%d",&x,&y);//找x和y的最小公倍数和最大公因数int lc,gc;lc = lcm(x,y);gc = gcd(x,y);printf("%d %d",lc,gc);return 0;
}2.辗转相除法(欧几里得法)
这是之前写的,现在写个更具模板化的
http://t.csdnimg.cn/s0mdb
#include<stdio.h>
#include<math.h>
#include<string.h>int gcd(int x,int y){int t;while(y){t = x % y;x = y;y = t;}return x;
}int lcm(int x,int y){return x*y/gcd(x,y);
}int main(){int x,y;scanf("%d%d",&x,&y);//找x和y的最小公倍数和最大公因数int lc,gc;lc = lcm(x,y);gc = gcd(x,y);printf("%d %d",lc,gc);return 0;
}辗转相除法,也称为欧几里得算法,是一种用于计算两个正整数最大公约数(Greatest Common Divisor, GCD)的古老而有效的算法。它的基本原理是利用了数学中的一个重要定理:对于任意两个整数a和b(假设a>b),它们的最大公约数与b和a除以b的余数c的最大公约数相同,即gcd(a, b) = gcd(b, c)。
以下是一个例子来说明辗转相除法的原理:
假设我们要找到15750和27216的最大公约数。
1. 首先,我们将较大的数27216除以较小的数15750,得到商1和余数11466(27216 = 1 × 15750 + 11466)。
2. 然后,我们将上一步的除数15750作为新的被除数,余数11466作为新的除数进行下一轮计算。将15750除以11466,得到商1和余数4284(15750 = 1 × 11466 + 4284)。
3. 接着,我们将上一步的除数11466作为新的被除数,余数4284作为新的除数进行下一轮计算。将11466除以4284,得到商2和余数3198(11466 = 2 × 4284 + 3198)。
4. 再次交换被除数和除数,将4284作为新的被除数,3198作为新的除数。将4284除以3198,得到商1和余数1086(4284 = 1 × 3198 + 1086)。
5. 继续这个过程,将3198作为新的被除数,1086作为新的除数。将3198除以1086,得到商3和余数22(3198 = 3 × 1086 + 22)。
6. 最后,将1086作为新的被除数,22作为新的除数。将1086除以22,得到商49和余数0(1086 = 49 × 22 + 0)。
由于我们已经得到了余数为0,这意味着当前的除数22就是原问题中两个数15750和27216的最大公约数。
所以,15750和27216的最大公约数为22。这就是辗转相除法的原理和一个实际应用的例子。通过反复进行除法和交换除数和余数的操作,直到余数为0,最后的除数就是两个原始数的最大公约数。
不会写?不要怕!
和我一起念口诀歪踢尔科斯歪尔科斯y,t,x,y,x,(



如何安装VITASHELL文件管理器)
)




 —— 接收数据和发送数据以及全局变量和浮点数)
、发送 接收批量消息(Java操作RocketMQ))






【尊嘟很详细】)


