文章目录
- 0 前言
- 1 课题简介
- 2 预测算法
- 2.1 Logistic回归模型
- 2.2 基于动力学SEIR模型改进的SEITR模型
- 2.3 LSTM神经网络模型
- 3 预测效果
- 3.1 Logistic回归模型
- 3.2 SEITR模型
- 3.3 LSTM神经网络模型
- 4 结论
- 5 最后
0 前言
🔥 优质竞赛项目系列,今天要分享的是
🚩 基于深度学习的新冠疫情预测算法研究与实现
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🥇学长这里给一个题目综合评分(每项满分5分)
- 难度系数:4分
- 工作量:4分
- 创新点:3分
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 课题简介
新型冠状病毒肺炎(COVID-19,简称“新冠肺炎”)疫情肆虐全球多个国家,本文采用新冠肺炎的时序历史数据,尝试利用Logistic回归模型、SEITR动力学模型、LSTM神经网络等数学模型预测疫情发展趋势与关键节点,对疫情的规模进行定量分析,对疫情原始基数和有效传播率进行科学和可靠的区间估算并进行不同算法的对比分析,为疫情防控中的分析、指挥和决策提供有效依据和指南。
2 预测算法
学长采用了三种算法对于疫情时序数据进行拟合:
- Logistic回归模型、
- SEITR动力学模型、
- LSTM神经网络。
2.1 Logistic回归模型
Logistic函数或Logistic曲线是一种常见的S形函数,它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。该模型广泛应用于生物繁殖和生长过程、人口增长过程模拟,因此也可以在一定程度上对病毒传播和确诊人数增长过程进行拟合。该函数常用的公式如下:
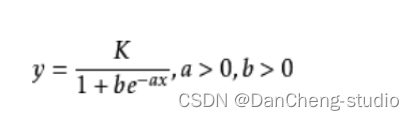
其中,a、b、K为皮尔模型的参数,估算这三个参数的方法有两类:一类是先估算出a和K,然后推算b值,如Fisher法;另一类是同时估算出参数a、b、K,如倒数总和法。结合疫情发生的实际场景,y为累计病例人数(例/天);t为时间(天);K、a、b为模型参数。从模型可知K为疫情规模,即累计病例最大值;a、b为控制传染速度的参数。
Logistic回归模型其算法思想来源于,当一个物种迁入到一个新生态系统中后,其数量会发生变化。假设该物种的起始数量小于环境的最大容纳量,则数量会增长。该物种在此生态系统中有天敌、食物、空间等资源也不足(非理想环境),则增长函数满足逻辑斯谛方程,图像呈S形,此方程是描述在资源有限的条件下种群增长规律的一个最佳数学模型。
其求参过程如下:根据实际统计的数据
y0,设定初始值K,计算y;用y’和t进行线性回归,得到参数a,b;根据K、a、b按上面的公式计算不同时间的预测值,并同步计算预测值与实际值之间的误差平方和;K值由原值加上步长重复计算,直到误差平方和到达最小,即最小二乘法寻优。此时的K值就是要找的最优K值。
2.2 基于动力学SEIR模型改进的SEITR模型
SEIR模型是一种动力学模型,是传染病预测最为常用的模型之一,所研究的传染病有一定的潜伏期,与病人接触过的健康人并不马上患病,而是成为病原体的携带者。与SIR模型相比,SEIR模型进一步考虑了与患者接触过的人中仅一部分具有传染性的因素,使疾病的传播周期更长。该模型将人口样本分为四类,分别为:易感者(S)、潜伏者(E)、传染者(I)和康复者(R),四类人群依次以一定比率进行转化或死亡,之间关系如下图所示:

其中四类人群具体如下:
1、S 类人群,易感者 (Susceptible),指未得病者,但缺乏免疫能力,与感染者接触后容易受到感染;
2、E 类人群,暴露者 (Exposed),指接触过感染者,但暂无能力传染给其他人的人,对潜伏期长的传染病适用;
3、I 类人群,感病者 (Infectious),指染上传染病的人,可以传播给 S 类成员,将其变为 E 类或 I 类成员;
4、R 类人群,康复者 (Recovered),指被隔离或因病愈而具有免疫力的人。如免疫期有限,R 类成员可以重新变为 S 类。
据此:可以得出SEIR模型的传染病动力学微分方程:
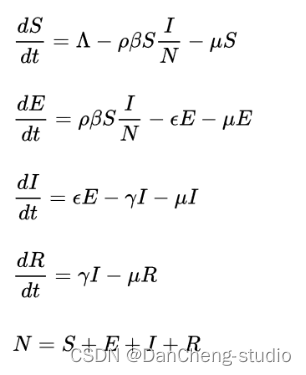
其中,ρ代表传染者单位时间接触易感者数量;β代表每名传染者与易感者接触传染病毒概率;μ代表单位时间死亡几率;ε代表单位时间潜伏者转变为传染者的几率;γ代表单位时间传染者痊愈的几率。
SEITR是基于SEIR模型改进的模型,在原有模型的基础上增加了修正的参数:
“T”:已被感染且正处于接受治疗时期的人群,主要特征表现为已被感染,已过潜伏期,但不会进行传染,且正在被治疗。
同时也将I人群严格定义为被感染,已过潜伏期但未被医院收治无法接受治疗的人群。
δ,表示I变为T的速率,主要受医院接诊速率及收治能力影响,也受发病后及时就医的时间影响。本文采用SEITR模型进行分析;
2.3 LSTM神经网络模型
长短期记忆人工神经网络(Long-Short Term Memory,
LSTM)是一种时间递归神经网络(RNN),由于独特的设计结构,LSTM适合于处理和预测时间序列中间隔和延迟非常长的重要事件。LSTM的拓扑图:
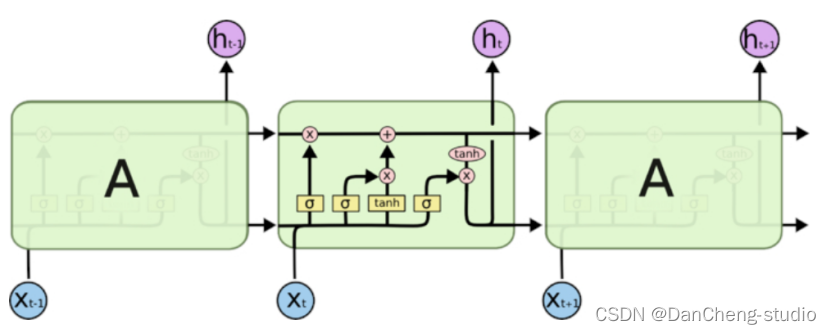
其公式如下:

3 预测效果
3.1 Logistic回归模型
定义logistic回归函数:def logistic_increase_function(t,K,P0,r):t0=11#r 0.05/0.55/0.65r = 0.45# t:time t0:initial time P0:initial_value K:capacity r:increase_rateexp_value=np.exp(r*(t-t0))return (K*exp_value*P0)/(K+(exp_value-1)*P0)
采用国内1月11日到1月27日的累计确诊病例数据作为原始数据,采用最小二乘法拟合逻辑斯蒂曲线,最后经过对逻辑斯蒂模型中R值(增长速率,到达K值的速度)的拟合调整,发现在0.45附近得到的曲线比较贴合我国1月至2月疫情实际情况。
预测参数:
K:capacity P0:initial_value r:increase_rate t:time[4.63653383e+04 3.69197450e+00 1.00000000e+00]
拟合图像:
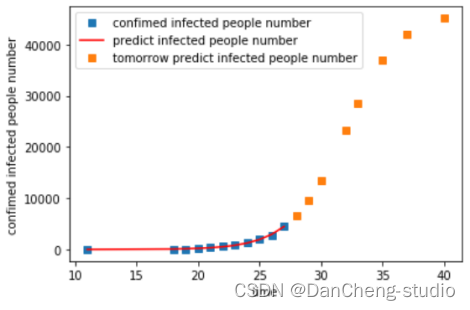
将拟合结果进行推广预测,得到2月9日的预测值在4万左右,与实际情况十分贴近,也证明了模型的一定可靠性;将本模型推广,进行全球范围内典型新冠肺炎爆发国家的疫情拟合与未来疫情预测,同时通过R值的大小,可以反应出该国疫情应对的有效程度。
对美国的当前确诊数据进行拟合:设置t0 = 11,r = 0.05
预测参数:
K:capacity P0:initial_value r:increase_rate t:time
[2.81881286e+06 7.54187927e+03 1.00000000e+00]
预测结果图像:

对德国的当前确诊数据进行拟合:设置t0 = 11,r = 0.094
预测参数:
K:capacity P0:initial_value r:increase_rate t:time
[1.80914161e+05 1.64581650e+02 1.00000000e+00]
预测结果图像:
3.2 SEITR模型
以下雪学长使用SEITR模型对美国疫情基本得到控制的时间进行预测:
定义SEIR函数:
def funcSEIR(inivalue,_):Y = np.zeros(5)X = inivalueY[0] = - (beta * X[0] *( X[2]+X[1])) / N # 易感个体变化Y[1] = (beta * X[0] *( X[2]+X[1])) / N - X[1] / Te # 潜伏个体变化Y[2] = X[1] / Te - δ * X[2] # 感染未住院Y[3] = gamma * X[4] # 治愈个体变化Y[4] = δ* X[2] - gamma* X[4] #治疗中个体变化
return Y
根据当前数值预估,可设置初始参数如下:
- N =330000000 # N为人群总数(美国人口大致为3.3亿)
- beta = 0.19 # β为传染率系数(美国实际应该略高)
- gamma = 0.15 # gamma为恢复率系数
- δ = 0.3 #δ为受到治疗系数(收治率)
- Te = 14 # Te为疾病潜伏期
- I_0 = 1 # I_0为感染未住院的初始人数
- E_0 = 0 # E_0为潜伏者的初始人数
- R_0 = 0 # R_0为治愈者的初始人数
- T_0 = 0 #T_0为治疗中的初始人数
- S_0 = N - I_0 - E_0 - R_0 - T_0 # S_0为易感者的初始人数
- T = 250 # T为传播时间
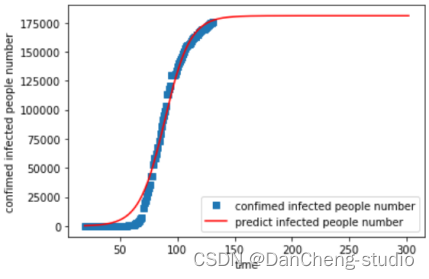
拟合结果:

本次预测得到的结果是今年秋季美国的疫情能够基本得到控制。
3.3 LSTM神经网络模型
这里采用了一个简单的LSTM模型,使用pytorch进行训练,对于世界疫情中确诊数据进行预测:model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_input, n_features)))
model.add(Dropout(0.15))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mse')
model.fit_generator(generator_conf,epochs=150)
对后一日的结果进行预测并绘图:
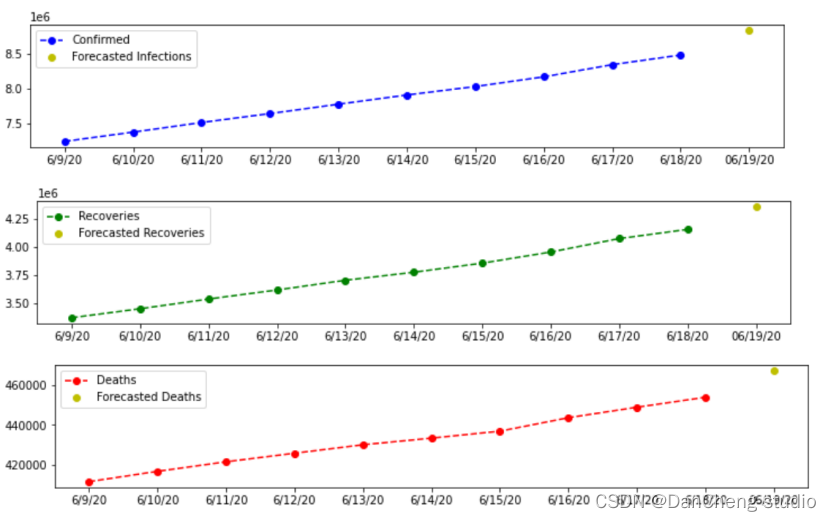
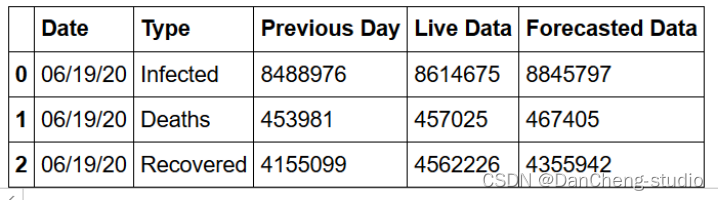
4 结论
总体来说,三种模型都能对新冠肺炎的时序数据作出一定的拟合,Logistic模型对于疫情控制措施没有较大改变的区域,或者是疫情已经初步得到控制的区域拟合还是效果相对较好的,但对于改变了疫情控制措施的地区来说还是过于粗糙,会造成较大的偏移;
LSTM在短期拟合数据较好,长期来看会有较大的偏移产生;
和其他流行病传染模型相比,SEIR
模型所研究的传染病具有一定的潜伏期,即与感染者接触过的易染者并不马上患病,而是成为病原体的携带者,本身具有一定的传染概率,该传播模式和2019-nCOV
更为吻合。
另外,我们对模型的假设条件是,美国的0号病人出现在今年1月11日,但是目前的报告陆续显示早在2019年美国就有社区性传播,因此模型对于此类具有较大不确定性地区的的可靠性大大下降。由于具体的时间目前国际上无法追溯,所以进一步的研究很难继续进行。
在SEIR模型中,还有以下几点需要注意:
1)传染率系数与人与人之间的社交距离和社交频率息息相关,美国在疫情早期未及时向民众宣传保持社交距离和戴口罩、减少出行的建议,导致传染率系数会比参数设置的更高;
2)治疗系数与当地医疗水平、卫生设施数量、医疗物资等息息相关,疫情中期各州的医疗设备全面告急,医护人员感染率上升,同时中产阶级及以下家庭因为无法支付高昂医疗费选择在家隔离,错过最佳治疗期,使得治疗系数要低于已经有雷神山火神山的武汉对应时期的治疗系数;
另外,SEIR模型在尝试同时拟合现有病例(正在接受治疗人群)和治愈人数曲线时,发现无法做到相对同时拟合的比较贴合实际的结果。参数设置对拟合结果的影响非常大,而模型参数的选择需要结合美国实际疫情情况才能推算,目前使用的计算手段过于粗糙。
参考资料
[1] 蔡洁等,基于SEIR模型对武汉市新型冠状病毒肺炎疫情发展趋势预测,山东医药
[2] 金启轩,中国新冠肺炎疫情预测建模与理性评估, 统计与决策
[3] 应用数学:群体免疫与SEIR模型,http://www.dataguru.cn/article-15472-1.html
5 最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
)
覆盖优化 - 附代码)

)





)






)


