📘北尘_：个人主页
🌎个人专栏:《Linux操作系统》《经典算法试题 》《C++》 《数据结构与算法》

☀️走在路上，不忘来时的初心

---

一、点名

1、题目讲解

2、算法原理

关于这道题中，时间复杂度为 O(N) 的解法有很多种，⽽且也是⽐较好想的，这⾥就不再赘述。
本题只讲解⼀个最优的⼆分法，来解决这个问题。
在这个升序的数组中，我们发现：
▪ 在第⼀个缺失位置的左边，数组内的元素都是与数组的下标相等的；
▪ 在第⼀个缺失位置的右边，数组内的元素与数组下标是不相等的。

3、代码实现

class Solution {
public:int takeAttendance(vector<int>& records) {int left=0,right=records.size()-1;while(left<right){int mid=left+(right-left)/2;if(records[mid]==mid) left=mid+1;else right=mid;}return records[left]==left?left+1:left;}
};

---

二、搜索旋转排序数组中的最⼩值

1、题目讲解

2、算法原理

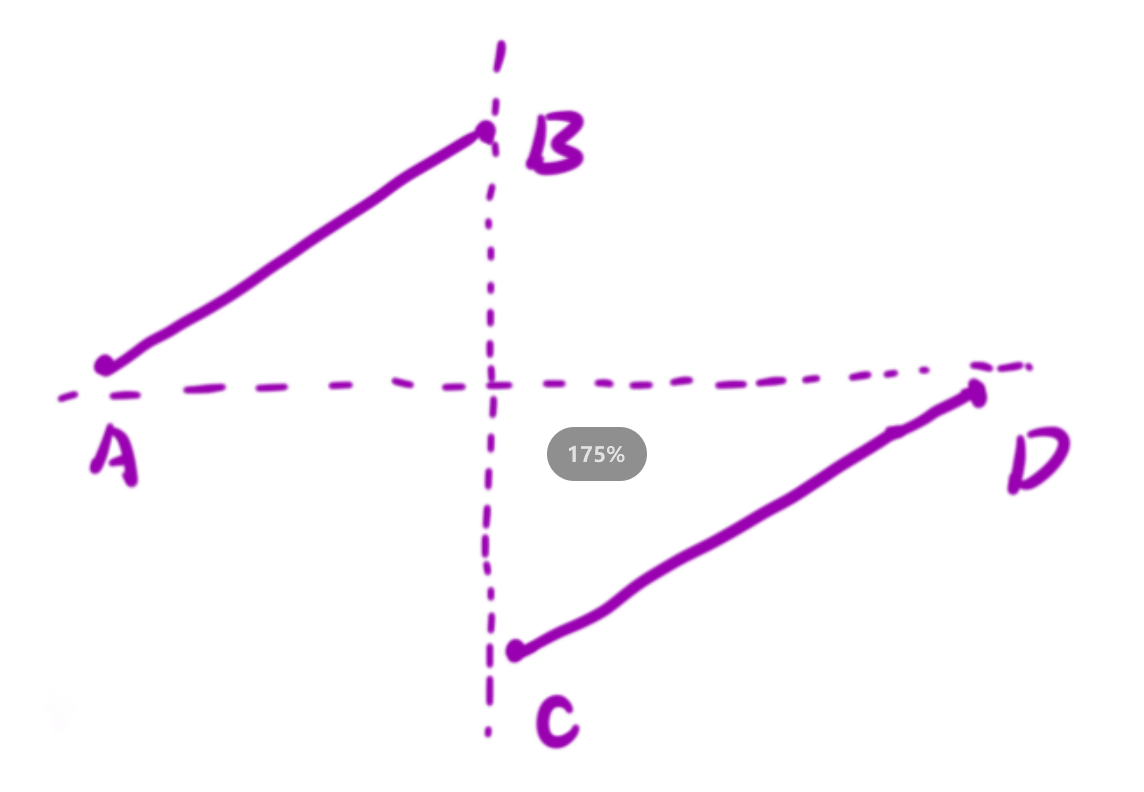
其中 C 点就是我们要求的点。
⼆分的本质：找到⼀个判断标准，使得查找区间能够⼀分为⼆。
通过图像我们可以发现， [A，B] 区间内的点都是严格⼤于 D 点的值的， C 点的值是严格⼩于 D 点的值的。但是当 [C，D] 区间只有⼀个元素的时候， C 点的值是可能等于 D 点的值的。
因此，初始化左右两个指针 left ， right ：
然后根据 mid 的落点，我们可以这样划分下⼀次查询的区间：
▪ 当 mid 在 [A，B] 区间的时候，也就是 mid 位置的值严格⼤于 D 点的值，下⼀次查询区间在 [mid + 1，right] 上；
▪ 当 mid 在 [C，D] 区间的时候，也就是 mid 位置的值严格⼩于等于 D 点的值，下次查询区间在 [left，mid] 上。
当区间⻓度变成 1 的时候，就是我们要找的结果。

3、代码实现

class Solution {
public:int findMin(vector<int>& nums) {int left=0,right=nums.size()-1,n=nums.size();while(left<right){int mid=left+(right-left)/2;if(nums[mid]>nums[n-1]) left=mid+1;else right=mid;}return nums[left];}
};

---

三、寻找峰值

1、题目讲解

2、算法原理

寻找⼆段性：
任取⼀个点 i ，与下⼀个点 i + 1 ，会有如下两种情况：
• arr[i] > arr[i + 1] ：此时「左侧区域」⼀定会存在⼭峰（因为最左侧是负⽆穷），那么我们可以去左侧去寻找结果；
• arr[i] < arr[i + 1] ：此时「右侧区域」⼀定会存在⼭峰（因为最右侧是负⽆穷），那么我们可以去右侧去寻找结果。

3、代码实现

class Solution {
public:int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<nums[mid+1]) left=mid+1;else right=mid;}return left;}
};

---

四、山峰数组的峰顶

1、题目讲解

2、算法原理

1. 分析峰顶位置的数据特点，以及⼭峰两旁的数据的特点：
   ◦ 峰顶数据特点： arr[i] > arr[i - 1] && arr[i] > arr[i + 1] ；
   ◦ 峰顶左边的数据特点： arr[i] > arr[i - 1] && arr[i] < arr[i + 1] ，也就是呈现上升趋势；
   ◦ 峰顶右边数据的特点： arr[i] < arr[i - 1] && arr[i] > arr[i + 1] ，也就是呈现下降趋势。
2. 因此，根据 mid 位置的信息，我们可以分为下⾯三种情况：
   ◦ 如果 mid 位置呈现上升趋势，说明我们接下来要在 [mid + 1, right] 区间继续搜索；
   ◦ 如果 mid 位置呈现下降趋势，说明我们接下来要在 [left, mid - 1] 区间搜索；
   ◦ 如果 mid 位置就是⼭峰，直接返回结果。

3、代码实现

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left=1,right=arr.size()-2;while(left<right){int mid=left+(right-left+1)/2;if(arr[mid]>arr[mid-1]) left=mid;else right=mid-1;}return left;}
};

---