文章目录
- 🍀树型结构
- 🐱👤什么是树型结构
- 🐱👓树型结构的概念
- 🐱🏍树的表示形式
- 🐱🐉树的应用
- 🌳二叉树
- 🐱👤二叉树的概念
- 🐱👓两种特殊的二叉树
- 🐱🏍二叉树的性质
- 🐱🐉二叉树性质练习
- 📌练习一
- 🚩解析:
- 📌练习二
- 🚩解析:
- 📌练习三
- 🚩解析:
- 📌练习四
- 🚩解析:
- ⭕总结

🍀树型结构
🐱👤什么是树型结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
-
有一个特殊的结点,称为根结点,根结点没有前驱结点
-
除根结点外,其余结点被分成M(M > 0)个互不相交的集合T1、T2、…、Tm,其中每一个集合Ti (1 <= i <=m) 又是一棵与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
-
树是递归定义的
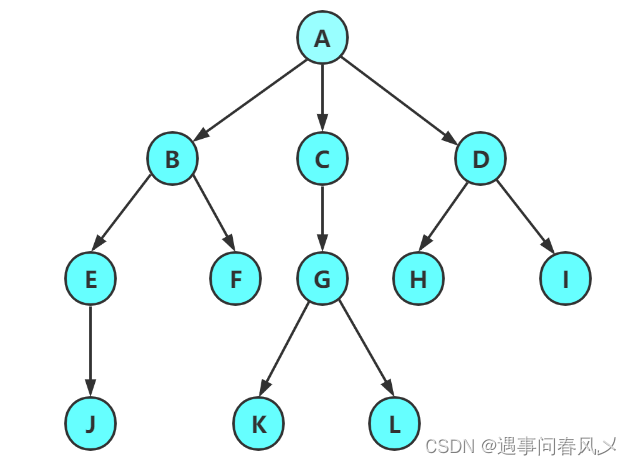
注意:树形结构中,子树之间不能有交集,否则就不是树形结构
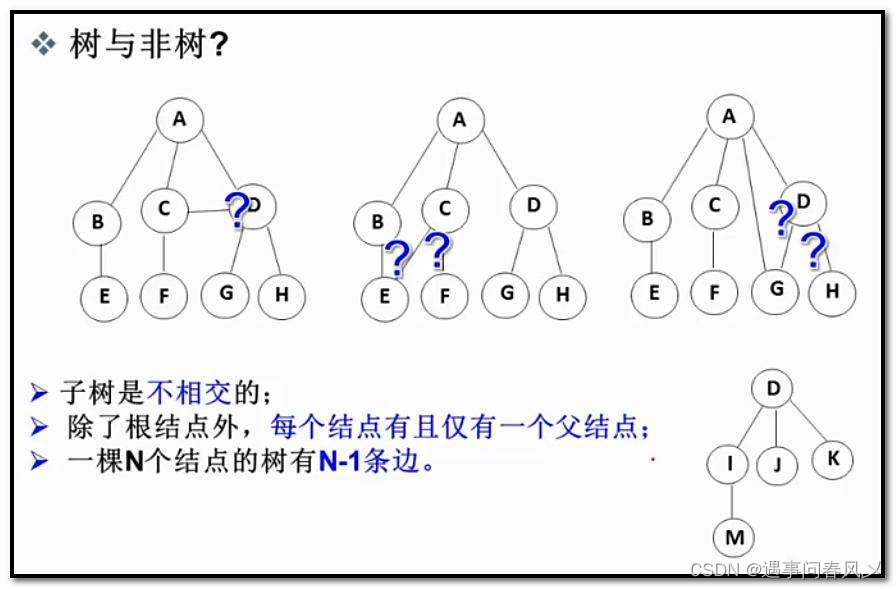
🐱👓树型结构的概念
对于下面这样一个树型结构,我们必须要明白如何描述它
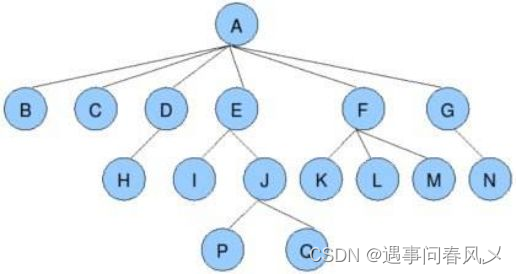
结点的度 :一个结点含有子树的个数称为该结点的度; 如上图:A的度为6
树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为6
叶子结点或终端结点:度为0的结点称为叶结点; 如上图:B、C、H、I…等节点为叶结点
双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点
根结点:一棵树中,没有双亲结点的结点;如上图:A
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推
树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
非终端结点或分支结点:度不为0的结点; 如上图:D、E、F、G…等节点为分支结点
兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:H、I互为兄弟结点
结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
森林:由m(m>=0)棵互不相交的树组成的集合称为森林
🐱🏍树的表示形式
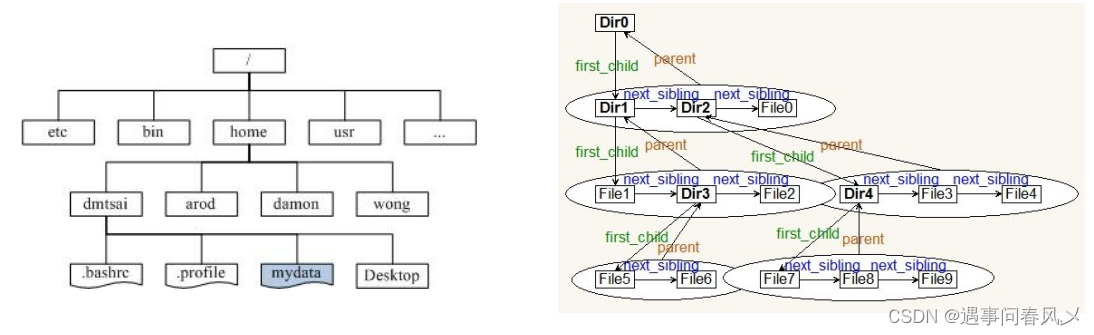
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法
使用如下:
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}
图解:
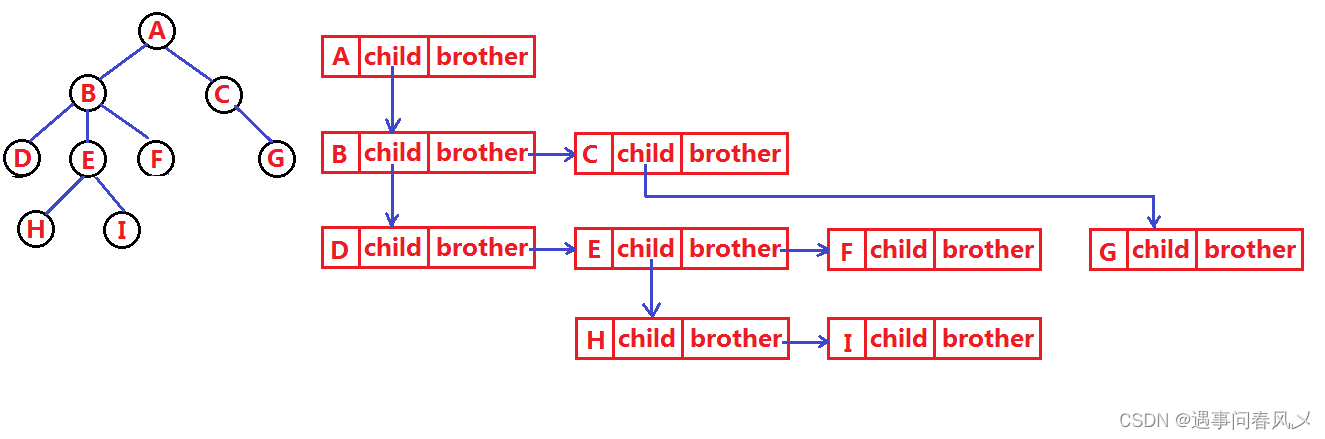
🐱🐉树的应用
如我们日常生活里的文件存储。文件系统管理(目录和文件)
🌳二叉树

🐱👤二叉树的概念
一棵二叉树是结点的一个有限集合,该集合:
-
或者为空
-
或者是由一个根节点加上两棵别称为左子树和右子树的二叉树组成。
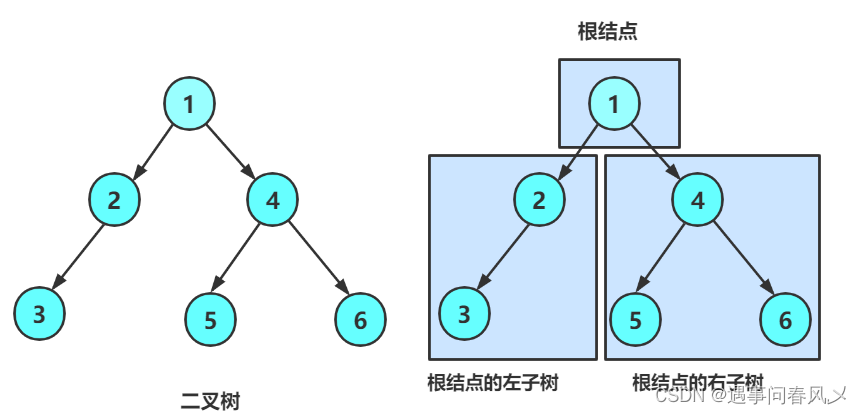
从上图可以看出:
-
二叉树不存在度大于2的结点
-
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
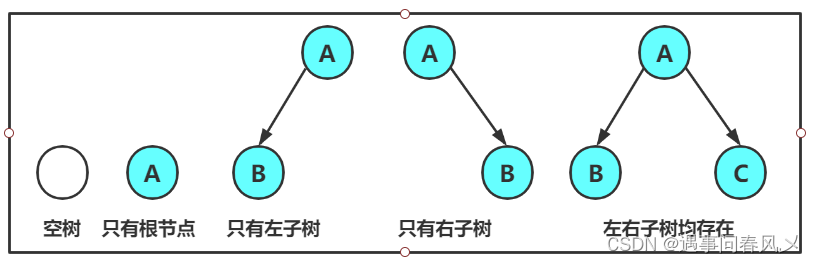
🐱👓两种特殊的二叉树
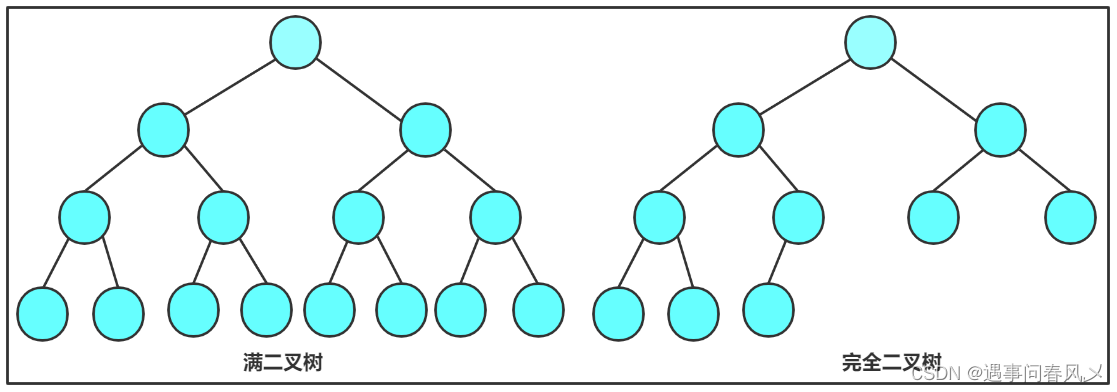
-
满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。
-
完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
🐱🏍二叉树的性质
-
若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有 (i>0)个结点
-
若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 (k>=0)
-
对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
-
具有n个结点的完全二叉树的深度k为

注意:向上取整 -
对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i的结点有:
若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
若2i+1<n,左孩子序号:2i+1,否则无左孩子
若2i+2<n,右孩子序号:2i+2,否则无右孩子
🐱🐉二叉树性质练习
📌练习一
- 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树 B 200
C 198 D 199
答案:B
🚩解析:
利用二叉树性质三:对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
所以叶结点 = 度为2的结点 + 1;为200,选B
📌练习二
- 在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n B n+1 C n-1 D n/2
答案:A
🚩解析:
2n个节点的完全二叉树,二叉树大概样子为如下:
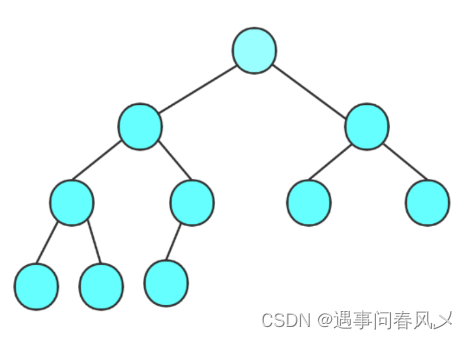
从上图我们可以得出:
- 度为1的节点:1个
度为0与度为2节点的个数不知道,但是我们知道度为二的节点数等于度为0的结点数减一,我们设度为0的结点为x
则有以下公式:
2n = x + x -1 +1;
解得:x = n;
所以选择A
📌练习三
- 一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383 B 384 C 385 D 386
答案:B
🚩解析:
这题与上题同理,只不过结点数为奇数
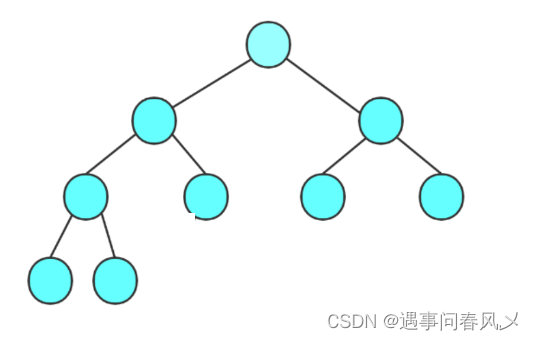
- 此时度为1的节点:1个
度为0与度为2节点的个数不知道,但是我们知道度为二的节点数等于度为0的结点数减一,我们设度为0的结点为x
则有以下公式:
767 = x + x -1;
解得:x = 384;
📌练习四
- 一棵完全二叉树的节点数为531个,那么这棵树的高度为( )
A 11 B 10 C 8 D 12
答案:B
🚩解析:
直接运用性质4
具有n个结点的完全二叉树的深度k为

注意:向上取整
所以答案为10,选B
⭕总结
关于《【数据结构】树与二叉树》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!












)


:并发测试(设置集合点))



